
1 сем 08 09 Линии и поверх в простр
.pdf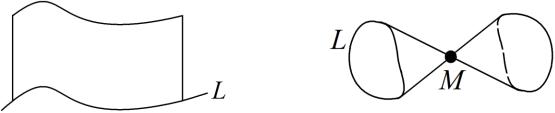
Линии и поверхности в пространстве
Уравнение F(x, y, z) 0 называется уравнением поверхности S в
прямоугольной декартовой системе координат Oxyz , если этому уравнению удовлетворяют координаты любой точки M (x, y, z) S , и не удовлетворяют координаты всех точек N(x, y, z) S .
Цилиндрической поверхностью (или цилиндром) называется поверхность
(рис. 1а), образованная прямыми, имеющими одинаковое направление и пересекающими некоторую кривую L . Прямые линии называются
образующими, а кривая L – направляющей цилиндра. Уравнение цилиндрической поверхности с образующими параллельными оси Oz ( Ox или Oy ) имеет вид F(x, y) 0 ( F( y, z) 0 или F(x, z) 0 соответственно).
Конической поверхностью (или конусом) называется поверхность (рис.
1б), образованная прямыми, проходящими через данную точку M и
пересекающими некоторую кривую L ( M L). Прямые линии называются
образующими, точка M – вершиной, а кривая L – направляющей конуса.
(а) |
(б) |
Рис. 1. Цилиндрическая (а) и коническая (б) поверхности.
Функция F(x, y, z) называется однородной функцией порядка (измерения
или степени) относительно переменных x, y, z , если при любом допустимом t R справедливо тождество
F(tx,ty,tz) t F(x, y, z) .
Уравнение конической поверхности в прямоугольной декартовой системе координат Oxyz с вершиной в точке O имеет вид F(x, y, z) 0 , где F(x, y, z)
– однородная функция.
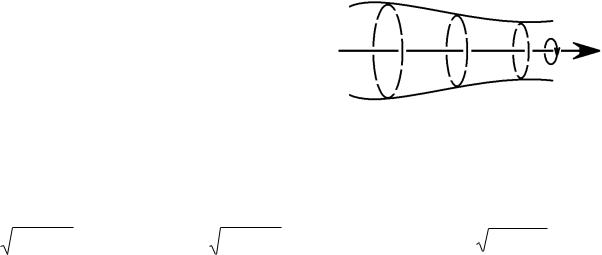
Поверхностью вращения (рис. 2)
называется поверхность, образованная вращением некоторой плоской кривой
вокруг оси, лежащей в еѐ плоскости. Если в |
|
||
прямоугольной |
декартовой |
системе |
|
координат Oxyz за ось вращения выбрать |
Рис. 2. Поверхность вращения. |
||
|
|||
ось Oz ( Ox |
или Oy ), то |
уравнение поверхности вращения имеет вид |
|
F ( x2 y2 , z) 0 |
( F ( |
y2 z2 , x) 0 |
или |
F( |
x2 z2 , y) 0 |
соответственно). |
|
|
|
|
|
Уравнения |
|
|
|
x x(u,v), |
|
|
|
|
(u,v) D R |
2 |
, |
y y(u,v), |
|
||
|
|
|
|
z z(u,v), |
|
|
|
называются параметрическими уравнениями поверхности S |
в прямоугольной |
||
декартовой системе координат |
Oxyz , если |
для всех |
(u,v) D точка |
M (x(u,v), y(u,v), z(u,v)) S и, для любой точки |
M0 (x0 , y0 , z0 ) S существует |
||
(u0 ,v0 ) D , что x0 x(u0 ,v0 ) , y0 |
y(u0 ,v0 ) , z0 |
z(u0 ,v0 ) . |
|
Уравнения
F1(x, y, z) 0,F2 (x, y, z) 0,
называются уравнениями линии L в прямоугольной декартовой системе координат Oxyz , если координаты любой точки M (x, y, z) L одновременно удовлетворяют обоим этим уравнениям, и не удовлетворяют хотя бы одному из данных уравнений координаты всех точек N(x, y, z) L . Каждое из уравнений
F1(x, y, z) 0 и F2 (x, y, z) 0
определяет некоторую поверхность в пространстве, а линия L является линией пересечения этих поверхностей.
Уравнения
x x(t), |
|
|
t D R , |
y y(t), |
|
|
|
z z(t), |
|
называются параметрическими уравнениями линии L в прямоугольной декартовой системе координат Oxyz , если для каждого значения t D точка
M (x(t), y(t), z(t)) L и, для любой точки M0 (x0 , y0 , z0 ) L существует такое значение t0 D , что x0 x(t0 ) , y0 y(t0 ) , z0 z(t0 ) . Эти уравнения могут быть записаны в виде одного векторного уравнения
r r(t) ,
где r – радиус-вектор точки M L, t – параметр.
Алгебраической поверхностью n -го порядка называется поверхность,
определяемая в некоторой прямоугольной декартовой системе координат алгебраическим уравнением n -ой степени. Если поверхность в некоторой прямоугольной декартовой системе координат определяется алгебраическим уравнением n -ой степени, то и в любой другой прямоугольной декартовой системе координат эта поверхность будет определяться алгебраическим уравнением той же n -ой степени.
Алгебраическими поверхностями первого порядка являются плоскости.
Плоскость в прямоугольной декартовой системе координат Oxyz можно задать уравнением одного из следующих видов.
1. Общее уравнение плоскости:
Ax By Cz D 0 ,
где A, B,C, D – произвольные действительные числа, причем A , B и C не равны нулю одновременно.
2. Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору:
A(x x0 ) B( y y0 ) С(z z0 ) 0,
где M0 (x0 , y0 , z0 ) – точка лежащая на плоскости, n( A, B,C) – вектор перпендикулярный плоскости (нормальный вектор).
3. Уравнение плоскости, проходящей через три заданные точки:
|
x x1 |
y y1 |
z z1 |
|
|
|
|||
|
x2 x1 |
y2 y1 |
z2 z1 |
0 , |
|
x3 x1 |
y3 y1 |
z3 z1 |
|
где M1(x1, y1, z1), M2 (x2 , y2 , z2 ) |
и M3 (x3, y3, z3 ) – точки принадлежащие |
|||
плоскости и не лежащие на одной прямой.
4.Нормальное уравнение плоскости:
xcos y cos z cos p 0,
где cos , cos и cos – направляющие косинусы нормального вектора,
направленного из начала координат в сторону плоскости, p – расстояние от начала координат до плоскости.

Для того чтобы общее уравнение плоскости привести к нормальному уравнению, необходимо уравнение умножить на множитель
|
|
|
|
|
|
1 |
|
|
|
, |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
A2 B2 C2 |
|||||||||
где знак «+» выбирается, если D 0 и знак «–», если D 0. |
||||||||||
5. Уравнение плоскости в отрезках: |
|
|
|
|||||||
|
|
x |
|
y |
|
z |
1, |
|
|
|
|
|
a |
b |
c |
|
|
||||
|
|
|
|
|
|
|
||||
где a , b и c – величины отрезков, которые плоскость отсекает на осях Ox , Oy
и Oz соответственно.
Расстояние h от точки M0 (x0 , y0 , z0 ) до плоскости, заданной общим
уравнением Ax By Cz D 0 определяется по формуле |
|
||||||||||||||||||||||||||||||||||
|
|
|
h |
|
|
Ax0 By0 |
|
Cz0 |
D |
|
|
|
. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пусть |
две |
плоскости |
|
|
заданы |
|
|
|
|
|
|
|
общими |
уравнениями |
|||||||||||||||||||||
A1x B1 y C1z D1 |
0 и A2 x B2 y C2 z D2 |
0 , тогда |
|
||||||||||||||||||||||||||||||||
а) плоскости параллельны, если |
|
A1 |
|
|
|
B1 |
|
|
|
C1 |
; |
|
|
|
|
||||||||||||||||||||
|
A2 |
|
B2 |
C2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
б) плоскости совпадают, если |
A1 |
|
|
|
B1 |
|
|
C1 |
|
|
D1 |
; |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
B2 |
|
|
|
|
C2 |
|
D2 |
|
|
|
|
|||||||||
в) плоскости перпендикулярны, если A1A2 B1B2 |
C1C2 |
0 ; |
|||||||||||||||||||||||||||||||||
г) угол между плоскостями определяется из равенства |
|
||||||||||||||||||||||||||||||||||
|
cos |
|
|
|
|
|
|
A1A2 B1B2 C1C2 |
|
|
, |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
A2 |
B2 C2 |
|
|
A2 |
B2 C2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
||||||

если требуется определить острый угол между плоскостями, то выражение в правой части равенства необходимо взять по модулю.
Прямую в пространстве в прямоугольной декартовой системе координат
Oxyz можно задать следующими уравнениями.
1.Общие уравнения прямой:
A1x B1 y C1z D1 0,A2 x B2 y C2 z D2 0,
где коэффициенты A1, B1,C1 не пропорциональны коэффициентам A2 , B2 ,C2 , то есть прямая является линией пересечения двух непараллельных плоскостей.
2. Уравнения прямой, проходящей через данную точку параллельно
заданному вектору (канонические уравнения прямой):
x x0 y y0 z z0 , |
||
ax |
ay |
az |
где M0 (x0 , y0 , z0 ) – точка лежащая на прямой, a(ax , ay , az ) – направляющий вектор прямой.
3. Уравнения прямой, проходящей через две заданные точки:
x x1 |
|
y y1 |
|
z z1 |
, |
|||||
|
|
|
||||||||
x |
x |
|
y |
2 |
y |
|
z |
2 |
z |
|
2 |
1 |
|
|
1 |
|
|
1 |
|
||
где M1(x1, y1, z1) и M2 (x2 , y2 , z2 ) – точки лежащие на прямой.
4. Параметрические уравнения прямой:
x x0y y0z z0
axt,
ayt, t R ,
azt,

где M0 (x0 , y0 , z0 ) – точка лежащая на прямой, a(ax , ay , az ) – направляющий
вектор прямой.
5. Векторно-параметрическое уравнение прямой: r(t) r0 at , t R ,
где r0 – радиус-вектор точки M0 L , a(ax , ay , az ) – направляющий вектор прямой, t – параметр.
Пусть две прямые заданы каноническими уравнениями
x x1 |
|
y y1 |
|
z z1 |
и |
x x2 |
|
y y2 |
|
z z2 |
, тогда |
|
|
|
|||||||||
|
|
|
|
|
|
||||||
ax |
|
ay |
|
az |
bx |
|
by |
|
bz |
||
а) прямые параллельны, если |
a |
x |
|
ay |
|
|
|
a |
z |
; |
|
|
|
|
||||
bx |
by |
|
bz |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) прямые перпендикулярны, если axbx ayby azbz |
0 ; |
|||||||||||||||||
в) угол между прямыми определяется из равенства |
|
|||||||||||||||||
cos |
|
|
axbx ayby azbz |
|
|
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a2 |
a2 |
a2 |
|
b2 |
b2 |
b2 |
|
|||||||||||
|
|
x |
|
y |
|
z |
|
|
x |
y |
z |
|
||||||
если требуется определить острый угол между прямыми, то выражение в правой части равенства необходимо взять по модулю;
г) прямые лежат в одной плоскости, если
|
x2 x1 |
y2 y1 |
z2 z1 |
|
|
ax |
ay |
az |
0 ; |
|
bx |
by |
bz |
|
|
|
|
|
|
д) прямые являются скрещивающимися, если 0 .

Пример 1. Найти угол между прямой |
3x y 4z 5 0, |
|
|
|
2 y 2z 3 0, |
и |
|
|
x |
|
|
плоскостью, проходящей через точки M1(2,3,1) , |
M2 ( 1,2,4) , M3 (0,4,3) . |
||||||||||||||||||||||||||||
Синус угла (рис. 3) между |
|
|
|
|
|
||||||||||||||||||||||||
прямой и плоскостью равен модулю |
|
|
|
|
|
||||||||||||||||||||||||
косинуса угла (модуль учитывает |
|
|
|
|
|
||||||||||||||||||||||||
случай, когда – тупой угол) между |
|
|
|
|
|
||||||||||||||||||||||||
нормальным вектором n плоскости и |
|
|
|
|
|
||||||||||||||||||||||||
направляющим вектором a прямой: |
|
|
|
|
|
|
|
||||||||||||||||||||||
sin |
|
cos |
|
|
|
|
|
|
na |
|
|
|
|
. |
(1) |
|
Рис. 3. Чертѐж к примеру 1. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
n |
|
|
|
a |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Выберем n M1M2 M1M3 , тогда |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
j |
k |
|
i |
|
j |
k |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
n |
1 2 |
|
|
2 3 |
4 1 |
|
3 |
1 |
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
0 2 |
|
|
4 3 |
3 1 |
|
2 1 2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2 3)i ( 6 6)j ( 3 2)k 5i 5k ( 5,0, 5) .
Общие уравнения прямой определяют две плоскости, пересечением которых является данная прямая. Следовательно, в качестве направляющего вектора a
можно выбрать |
a n1 n2 , где |
n1 и |
n2 – нормальные векторы указанных |
||||||||||||||||||||||||||
плоскостей. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a |
3 |
1 |
4 |
(2 8)i ( 4 6)j (6 1)k 10i 10 j 5k (10, 10,5) . |
|||||||||||||||||||||||||
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя координаты векторов n и a в формулу (1), находим |
|
|
|
|
|
|
|||||||||||||||||||||||
sin |
|
|
|
( 5) 10 0 ( 10) ( 5) 5 |
|
|
|
|
|
|
75 |
|
|
|
1 |
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 225 |
|
|
||||||||||||
|
|
|
|
( 5)2 02 ( 5)2 |
102 |
( 10)2 |
52 |
2 |
|
|
|||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
sin |
|
1 |
|
|
|
. ▲ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||

Уравнение алгебраических поверхностей 2-го порядка в прямоугольной декартовой системе координат Oxyz имеет вид
Ax2 By2 Cz2 2Dxy 2Exz 2Fyz Gx Hy Iz J 0 , |
(2) |
где не все коэффициенты A , B , C , D , E , F равны одновременно нулю.
Вобщем случае уравнение (11) может определять: 1) пустое множество,
2)точку, 3) прямую, 4) плоскость, 5) пару плоскостей, 6) эллипсоид, 7)
гиперболоид, 8) конус второго порядка, 9) параболоид, 10) цилиндр второго порядка. В случаях 1) – 5) алгебраические поверхности 2-го порядка называются вырожденными, остальные невырожденными.
В пространстве всегда можно выбрать такую прямоугольную декартову систему координат Oxyz , в которой любое уравнение, определяющее невырожденную поверхность 2-го порядка, приведется к одному из следующих видов.
Уравнение эллипсоида
x2 |
|
y2 |
|
z2 |
1, |
( a 0 , b 0, c 0). |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
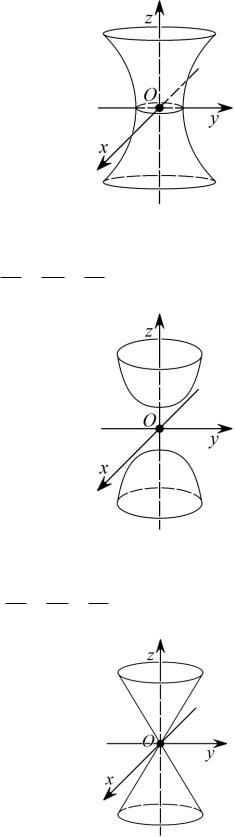
Уравнение гиперболоида
а) однополостного
x2 |
|
y2 |
|
z2 |
1, |
( a 0 , b 0, c 0). |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
б) двуполостного
x2 y2 z2 1, ( a 0 , b 0, c 0). a2 b2 c2
Уравнение конуса второго порядка
x2 y2 z2 0 , ( a 0 , b 0, c 0). a2 b2 c2
