
1 сем 13 14 Предел последоват и функции
.pdfЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Числовой последовательностью называется функция f : N R . Число-
вая последовательность обозначается
{xn} x1, x2 , , xn , ,
где каждое значение xn f (n) , n N называется элементом (или членом) по-
следовательности {xn }, а число n – его номером. Формула xn f (n) называ-
ется формулой общего члена последовательности.
Заметим, что множество элементов последовательности всегда бесконеч-
но (счѐтно), а множество значений элементов может быть конечным. Например,
|
1 |
1, |
1 |
, |
1 |
, , |
1 |
, , |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
n |
|
2 |
|
3 |
|
n |
|
|||
|
n |
1, 0, |
1, 0, 1, 0, |
1, |
0, |
sin |
|
||||
|
2 |
|
|
|
|
Последовательность называется ограниченной сверху (снизу), если
|
|
|
|
|
|
|
|
|
C R n N: xn C ( xn C ). |
|||||
Последовательность ограниченная сверху и снизу называется ограниченной. |
||||||||||||||
Последовательность, не являющаяся ограниченной (сверху или снизу) на- |
||||||||||||||
зывается неограниченной (сверху или снизу). |
||||||||||||||
Например, |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
||||
|
|
|
1, |
|
, |
|
|
|
, , |
|
|
, |
– ограниченная последовательность, |
|
|
|
|
|
|
|
|
||||||||
n |
|
2 |
|
3 |
|
|
|
n |
|
|
||||
{n} |
1, |
2, |
3, |
, |
n, |
– |
последовательность ограниченная снизу |
|||||||
|
|
|
|
|
|
|
|
|
|
и неограниченная сверху, |
||||
|
|
n |
1, |
0, |
|
3, 0, 5, 0, 7, 0, – неограниченная |
||||||||
|
nsin |
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
последовательность.
Над числовыми последовательностями можно выполнять следующие арифметические действия.
1) Произведением последовательности {xn } на число k R называется последовательность
{kxn} kx1, kx2 , , kxn ,
2) Суммой последовательностей {xn } и {yn} называется последователь-
ность
{xn yn} x1 y1, x2 y2 , , xn yn ,
3) Разностью последовательностей {xn} и {yn} называется последова-
тельность
{xn yn} x1 y1, x2 y2 , , xn yn ,
4) Произведением последовательностей {xn } и {yn} называется после-
довательность
{xn yn} x1 y1, x2 y2 , , xn yn ,
5) Частным последовательностей {xn } и {yn} называется последова-
тельность
|
|
|
|
|
|
x1 |
|
x2 |
|
|
xn |
|
|
|
|
|
|
|
xn |
|
|
|
, |
, , |
|
, ( yn 0, n N ). |
|||||||||
|
|
|
|
|
|
|
|||||||||||
yn |
|
|
y1 |
y2 |
|
yn |
|||||||||||
Число a называется пределом последовательности {xn }, если |
|||||||||||||||||
|
|
|
|
0 N N( ) n N : |
|
xn a |
|
, |
|||||||||
|
|
|
|
|
|
||||||||||||
и обозначают lim xn a или xn a |
при n . |
||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неравенство |
|
xn a |
|
равносильно неравенству |
|||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
a xn a , |
||||||||
откуда следует геометрический смысл (рис. 1) предела последовательности:
число a является пределом последовательности {xn }, если в любой его окрест-
ности O(a) содержится бесконечное число членов последовательности {xn}, а

вне окрестности O(a) находится лишь конечное число элементов последова-
тельности {xn }.
Рис. 1. Геометрический смысл предела последовательности.
Последовательность {xn } называется бесконечно большой, если
M 0 N N(M ) n N : |
|
xn |
|
M , |
|
|
|
||||
и обозначают lim xn . |
При выполнении |
неравенства xn M (или |
|||
n |
|
|
|
|
|
xn M ) записывают lim xn (или lim xn ). |
|||||
n |
n |
|
|
|
|
Пусть {xn } и {yn} |
– бесконечно большие последовательности и |
||||
lim xn lim yn , а {cn} – ограниченная последовательность. Тогда бес-
n n
конечно большими будут последовательности {xn yn}, {xn yn}, {cn xn},
{cn xn}.
Последовательность { n} называется бесконечно малой, если0 N N( ) n N : n ,
то есть lim n 0 .
n
1 Например, последовательность является бесконечно малой при
na a 0 и бесконечно большой при a 0 .
Если последовательности { n} и { n} бесконечно малые, то бесконечно малыми будут последовательности { n n}, { n n}, {cn n}, где {cn} –
ограниченная последовательность. Если { n} – бесконечно малая последова-
1 тельность, то – бесконечно большая последовательность.
n
Последовательность, имеющая конечный предел, называется сходящейся,
в противном случае – расходящейся. Также в этих случаях говорят, последова-
тельность сходится либо расходится.
Сходящиеся последовательности обладают следующими свойствами. 1) Сходящаяся последовательность имеет только один предел.
2) Сходящаяся последовательность ограничена. Обратное утверждение может быть неверно.
3) Если lim xn a , то любой элемент xn последовательности {xn } мож-
n
но представить в виде xn
довательности { n}.
4) Если lim xn a ,
n
lim (xn yn ) a b ,
n
a n , где n – элемент бесконечно малой после-
lim yn b , то |
|
|
|
|
|
|
|
|
||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
lim (x |
y |
|
) ab, |
lim |
xn |
|
a |
( y |
|
0, b 0). |
||
n |
|
|
n |
|||||||||
n |
n |
|
|
n y |
|
|
b |
|
||||
|
|
|
|
n |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5) Если элементы последовательности {xn}, начиная с некоторого номе-
ра, удовлетворяют неравенству xn a ( xn a ), то lim xn |
a ( lim xn a ). |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
||||||
6) Если элементы последовательностей {xn}, {yn}, {zn } начиная с неко- |
||||||||||||||||||||||||||||
торого номера, удовлетворяют неравенству xn yn zn и |
lim xn lim zn a , |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|||||
то lim yn a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 1. Вычислить пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а) lim |
1 3n 4n2 |
|
б) lim |
|
6 7n2 |
|
, в) lim |
3 4n 5n2 |
|
|||||||||||||||||||
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||
n 3 5n 2n2 |
|
n 1 |
2n |
n3 |
|
|
n |
|
|
|
8 9n |
|
||||||||||||||||
а) Поделим в пределе числитель и знаменатель дроби |
|
1 3n 4n2 |
на |
|||||||||||||||||||||||||
3 |
5n 2n2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
старшую степень величины n , то есть на n2 . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3n |
|
|
4n2 |
|
||||||
|
1 3n 4n2 |
|
(1 3n 4n2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
lim |
n2 |
|
|
lim |
|
n2 |
|
n2 |
n2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
n 3 5n 2n2 |
n |
|
|
|
2 |
1 |
|
|
n |
3 |
|
|
5n |
2n2 |
|
|||||||||||||
|
|
|
|
|
(3 5n 2n |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
n2 |
|
n2 |
n2 |
|
||||||||||||||
|
|
1 |
|
3 |
4 |
|
|
|
|
|
n2 |
n |
4 |
|
|||
lim |
|
|
|
|
2 . |
|||
|
3 |
|
5 |
|
2 |
|||
n |
|
2 |
|
|||||
|
|
n2 |
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(6 7n2 ) |
1 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
7n2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
6 7n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
б) lim |
|
lim |
n |
3 |
|
|
|
|
|
lim |
|
|
|
|
n |
3 |
|
n |
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
2n n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 2n n3 |
|
|
||||||||||||||||||||||||||||||
n 1 |
n |
(1 2n n |
3 |
) |
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
n3 |
n3 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
n3 |
|
n |
|
|
|
|
0 |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
n3 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
4n |
|
|
|
5n2 |
|
|||||||||||||||||
|
3 4n 5n2 |
|
lim |
(3 4n |
|
5n2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
в) lim |
|
n2 |
|
lim |
|
|
n2 |
|
n2 |
|
|
n2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8 9n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
8 9n |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(8 9n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
n2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
lim |
|
|
|
|
n2 |
|
n |
|
. ▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пусть задана числовая последовательность {xn }. Составим из еѐ элемен- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тов с номерами k1, k2 , , km , ( k1 |
|
k2 |
|
km ) новую последователь- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{xkm } xk1 , xk2 , , xkm ,
Числовая последовательность {xkm } называется подпоследовательностью ис-
ходной последовательности {xn }.
Например, {x |
} 1, |
1 |
, |
|
1 |
, |
|
, |
|
1 |
, имеет подпоследовательности |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
n |
|
|
2 |
|
3 |
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
{x |
|
} |
1 |
, |
|
1 |
|
, |
1 |
, , |
|
1 |
, |
||||||||||||
|
k |
|
|
|
|
|
||||||||||||||||||||
|
|
m |
2 |
4 |
|
6 |
|
|
2m |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
{x } |
1 |
, |
1 |
, |
1 |
, , |
1 |
|
|
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
lm |
|
|
|
|
4 |
|
|
|
9 14 |
|
|
|
5m 1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||

Число a называется частичным пределом последовательности {xn }, если найдѐтся подпоследовательность последовательности {xn }, предел которой ра-
вен a . Если последовательность {xn } сходится и lim xn a , то любой еѐ час-
n
тичный предел равен a . Для расходящихся последовательностей частичные пределы могут принимать различные значения.
Наибольший из всех частичных пределов последовательности {xn} назы-
вается верхним пределом последовательности {xn } и обозначается lim xn , а
n
наименьший, соответственно, нижним пределом последовательности {xn }, и |
|||||||||
обозначается lim xn . |
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
||
|
|
|
|
|
n |
1, |
0, 1, 0, 1, 0, |
1, 0, |
|
Например, последовательность sin |
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
имеет три частичных предела a1 1, a2 |
0 , a3 1. Тогда |
|
|||||||
|
|
|
n 1 и |
|
lim sin n |
1. |
|
||
|
lim sin |
|
|
||||||
n |
2 |
|
n |
2 |
|
|
|||
Числовая последовательность {xn } называется:
1)возрастающей, если n N : xn xn 1 ;
2)неубывающей, если n N : xn xn 1 ;
3)убывающей, если n N : xn xn 1;
4)невозрастающей, если n N : xn xn 1 .
Такие последовательности называются монотонными. Последовательно-
сти 1) и 2) называются монотонно возрастающими, а последовательности 3) и
4) – монотонно убывающими.
Теорема 1. Монотонно возрастающая (убывающая) последовательность
{xn } сходится тогда и только тогда, когда она ограничена сверху (снизу). Для монотонно возрастающей (убывающей) последовательности
lim xn sup{xn} |
( lim xn inf{ xn}). |
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|||
Пример 2. Доказать, что последовательность {xn }, где xn |
|
1 |
|
схо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||
дится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Покажем, что последовательность {xn } возрастающая и ограничена |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сверху. Воспользуемся формулой бинома Ньютона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
(a b)n |
Cnk an k bk , |
|
где Cnk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k!(n k)! |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
n 1 |
|
|
|
n(n 1) |
|
|
n 2 |
|
|
|
|
2 |
|
|
|
|
n(n 1)(n 2) |
|
|
|
|
n 3 |
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
(a b) |
|
a |
|
|
na |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n(n 1) 2 1 |
|
bn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Запишем выражения для xn и xn 1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n(n 1) |
|
|
1 |
|
|
|
|
|
|
n(n 1)(n 2) |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
xn |
1 |
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
n |
n |
|
|
|
|
|
|
2! |
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
n3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n(n 1) [n (n 1)] |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|||||||||||||||||||||||||||||
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
, |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2! |
|
|
|
|
n |
|
|
|
|
3! |
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
xn 1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
3! |
|
|
|
|
|
1 |
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n! |
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n |
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Нетрудно видеть, что 1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
при 0 |
k n , поэтому каждое |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
слагаемое в xn 1 будет больше соответствующего слагаемого в xn , и кроме то-
го, xn 1 содержит на одно положительное слагаемое больше, чем xn . Следова-
тельно, при любом n N : xn xn 1 , то есть {xn } возрастающая последова-
тельность.
|
|
|
k |
1 |
|
1 |
|
|
1 |
(n 2) |
|
|
Далее учтѐм, что в |
xn все скобки 1 |
|
|
и |
|
|
|
. Тогда |
||||
|
|
|
2n 1 |
|||||||||
|
|
|
n |
|
|
n! |
|
|
|
|||
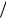
x |
|
2 |
1 |
|
|
1 |
|
1 |
1 1 |
1 |
|
1 |
|
|
1 |
|
||||||||||
n |
|
|
|
|
|
|
2n 1 |
|||||||||||||||||||
|
|
|
|
|
2! 3! |
|
n! |
|
2 22 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 1 |
1 |
|
|
1 |
|
|
1 |
|
|
1 |
1 |
|
1 |
1 2 3 . |
||||||||||||
|
|
22 |
|
2n 1 |
2n |
|
1 2 |
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
Полученное неравенство означает, что последовательность {xn} ограничена сверху.
|
|
1 n |
||
Таким образом, последовательность {xn }, где xn 1 |
|
|
|
является мо- |
|
||||
|
|
n |
|
|
нотонно возрастающей и ограниченной сверху. Следовательно, по теореме 1
последовательность {xn } сходится. Предел этой последовательности представ-
ляет собой иррациональное число, обозначаемое
|
|
1 n |
|
|
e lim 1 |
|
|
|
2,7182818284 59045 |
|
||||
n |
|
n |
|
|
Это число является основанием натуральных логарифмов. ▲
ПРЕДЕЛ ФУНКЦИИ
1. Предел функции в точке и на бесконечности
Точка x0 называется предельной точкой множества D R , если в любой окрестности точки x0 есть точки x D (сама точка x0 может, как принадле-
жать, так и не принадлежать множеству D ).
Пусть x0 предельная точка множества D R и пусть на множестве D
определена функция f (x) , причѐм в точке x0 функция может быть определена,
а может и не определена.
Определение 1 (по Гейне). Число b называется пределом функции f (x) в
точке x0 , если для любой сходящейся к x0 |
последовательности {xn} точек |
||||
множества D , все элементы которой xn x0 , |
соответствующая последователь- |
||||
ность значений функции { f (xn )} сходится к числу b . |
|||||
Для обозначения предела функции |
f (x) |
в точке x0 используется обозна- |
|||
чение |
|
|
|
|
|
lim f (x) b или |
f (x) b при x x0 . |
||||
x x0 |
|
|
|
|
|
Определение 2 (по Коши). Число b называется пределом функции f (x) в |
|||||
точке x0 , если |
|
|
|
|
|
|
|
|
f (x) b |
|
. |
|
|
|
|||
0 ( ) 0 x O (x0 ) D : |
|
||||
Теорема 1. Определения предела функции по Гейне и по Коши эквива- |
|||||
лентны. |
|
|
|
|
|
Число b называется правым (левым) пределом функции f (x) в точке x0 ,
если для любой сходящейся к x0 последовательности {xn } точек множества D ,
все элементы которой xn x0 ( xn x0 ), соответствующая последовательность значений функции { f (xn )} сходится к числу b .
Правый и левый пределы называются односторонними пределами, для них используются обозначения:
lim |
f (x) |
или |
lim |
|
f (x) или |
f (x0 0) – для правого предела, |
x x0 |
|
|
x x0 |
0 |
|
|
lim |
f (x) |
или |
lim |
f (x) или |
f (x0 0) – для левого предела. |
|
x x0 |
|
x x0 |
|
0 |
|
|
Связь между односторонними пределами и пределом функции в точке ус-
танавливает следующая теорема.
Теорема 2. Функция f (x) имеет в точке x0 предел тогда и только тогда,
когда в этой точке существуют как правый, так и левый пределы и они равны. В
этом случае |
lim f (x) |
lim |
|
|
f (x) lim |
f (x) . |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x x0 |
|
|
|
|
|
x |
x0 |
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 1. Вычислить пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
а) lim |
|
x 5 |
|
, |
|
б) lim |
x2 3x 2 |
, |
в) lim sign x , |
г) lim sin |
1 |
. |
|||||||||||||||||||
|
x2 |
7 |
|
x2 |
x 2 |
x |
|||||||||||||||||||||||||
x 3 |
|
|
|
|
x 1 |
|
|
x 0 |
|
|
|
|
x 0 |
|
|
|
|||||||||||||||
а) lim |
|
x 5 |
|
|
|
3 5 |
|
|
8 |
|
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x 3 x2 7 |
|
|
|
32 7 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б) lim |
x2 |
3x 2 |
lim |
|
(x 1)(x 2) |
lim |
x 2 |
|
1 2 |
|
1 |
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x2 |
|
x 2 |
|
(x 1)(x 2) |
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
x 1 |
|
|
x 1 |
|
x 1 x 2 |
|
1 |
|
3 |
|
|
|
|||||||||||||||||||
в) Функция y sign x |
|
|
определяется равенст- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1, x 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0, x 0, |
Очевидно, что lim sign x 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
вом sign x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
1, x 0.
и lim sign x 1, следовательно, по теореме 2 функ-
x 0
ция y sign x не имеет предела при x 0.
