
09 Системы ОДУ
.pdf
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Нормальной системой n дифференциальных уравнений первого порядка с неизвестными функциями y1 x , y2 x , , yn x называется система вида
|
|
|
|
|
|
y |
f |
x, y , |
y |
, ..., y |
n |
, |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f2 x, y1, y2 , ..., yn , |
|
|
|
|||||
|
|
|
|
|
|
y2 |
|
|
|
|||||||
|
|
|
|
|
|
.................................. |
|
|
|
(1) |
||||||
|
|
|
|
|
|
|
|
fn x, y1, y2 , ..., yn , |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
yn |
|
|
|
|||||||
|
|
|
|
|
|
|
Rn 1 |
|
||||||||
где функции |
f |
i |
, |
i 1, n , определены в некоторой области D пространства |
пере- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
менных x, y1 , y2 , , yn . Число n называется порядком нормальной системы. |
|
|
||||||||||||||
Решением (частным решением) нормальной системы (1) на отрезке [a, b] |
назы- |
|||||||||||||||
вается совокупность n функций |
y1 y1 x , |
y2 y2 x , , |
yn yn x , непрерывно |
|||||||||||||
дифференцируемых на [a, b] , а также обращающих эту систему уравнений в тождества.
|
|
Кривая в пространстве |
Rn 1 |
переменных x, y , y |
, , |
y |
n |
, соответствующая ре- |
||||||||||
шению y1 y1 x , y2 y2 x , , yn |
|
|
|
|
|
1 |
2 |
|
|
|
||||||||
yn x нормальной системы (1), называется инте- |
||||||||||||||||||
гральной кривой этой системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Общим решением нормальной системы (1) на отрезке [a, b] будем называть |
||||||||||||||||
множество всевозможных частных решений этой системы. |
|
|
|
|||||||||||||||
|
|
Задача Коши для системы (1) формулируется следующим образом: найти реше- |
||||||||||||||||
ние |
y1 y1 x , y2 |
y2 x , , yn |
yn x |
этой системы, |
удовлетворяющее начальным ус- |
|||||||||||||
ловиям |
|
|
x |
|
|
|
x |
y0 , ..., |
|
|
x |
y0 |
|
|
|
|||
|
|
|
|
y |
y0 , |
y |
2 |
y |
n |
, |
|
|
||||||
|
|
|
|
1 |
0 |
1 |
|
0 |
2 |
|
0 |
|
n |
|
|
|
||
где |
y0 |
, y0 |
, ..., y0 |
– заданные числа. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема (о существовании и единственности решения задачи Коши для нор- |
||||||||||||||||
мальной системы дифференциальных уравнений). |
Если функции fi x, y1 , y2 , , yn , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
пространства Rn 1 |
||||||
i 1, n |
|
ограничены и непрерывны |
|
в области |
D |
|
|||||||||
x, y1 , y2 |
, , yn , то система (1) имеет хотя бы одно решение |
y1 y1 x , |
|||||||||||||
yn yn |
x , удовлетворяющее начальным условиям |
|
|
|
|
||||||||||
|
|
|
|
y |
x |
y0 , |
y |
2 |
x |
y0 , |
..., y |
n |
x |
y0 |
, |
|
|
|
|
1 |
0 |
1 |
|
0 |
2 |
|
0 |
n |
|
||
переменных y2 y2 x , ,
где x0 , y10 , y20 , , yn0 – любая точка области D . Если, кроме того, частные производные fi 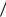 yk , i, k 1, n существуют и ограничены в области D , то имеет место единственность данного решения.
yk , i, k 1, n существуют и ограничены в области D , то имеет место единственность данного решения.
1

Таким образом, при выполнении условий теоремы о существовании и единственности решения задачи Коши для нормальной системы дифференциальных уравне-
ний в некоторой области D пространства Rn 1 переменных x, y1 , y2 , , yn через каждую точку x0 , y10 , y20 ,..., yn0 этой области проходит одна и только одна интегральная кривая системы уравнений (1). Следовательно, при каждом фиксированном x0 общее решение нормальной системы (1) зависит от n параметров. В качестве этих параметров могут выступать значения искомых функций в точке x0 . Поэтому общее решение системы уравнений (1) может быть записано в виде
y1 1 x,C1 ,C2 , ,Cn , y2 2 x,C1 ,C2 , ,Cn ,
……………………
yn n x,C1 ,C2 , ,Cn ,
где C1 ,C2 , ,Cn – произвольные постоянные.
Любое дифференциальное уравнение n -го порядка
y |
n |
|
|
n 1 |
|
(2) |
|
f x, y, y , y |
, , y |
|
можно свести к нормальной системе дифференциальных уравнений. В самом деле, положим
y1 y , |
y2 y |
|
, |
|
|
|
|
yn y |
n 1 |
. |
(3) |
|||
|
y3 y , , |
|
||||||||||||
Тогда уравнение (2) примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f x, |
y1 , y2 , , yn |
. |
|
|
(4) |
||||||||
yn |
|
|
||||||||||||
Таким образом, уравнение (2) с учетом равенств (3) и (4) эквивалентно нормаль- |
||||||||||||||
ной системе дифференциальных уравнений |
|
|
|
|
|
|
|
|
||||||
y |
y |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 , |
|
|
|
|
|
|
|
|
|
|||
y2 |
|
|
|
|
|
|
|
|
|
|||||
................... |
|
|
|
|
(5) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
yn 1 yn |
|
|
|
|
|
|
|
|
||||||
y |
f x, |
y , y |
2 |
, ..., y |
n |
. |
|
|
|
|||||
|
n |
|
|
|
|
|
1 |
|
|
|
|
|
||
Обратно, пусть задана нормальная система дифференциальных уравнений (87), где функции fi , i 1, n n раз непрерывно дифференцируемы в рассматриваемой об-
ласти D . Эту систему, можно свести к одному дифференциальному уравнению порядка n . На этом основан один из методов интегрирования систем дифференциальных уравнений – метод исключения.
2

Пример. Решить методом исключения задачу Коши
y 3y 4z, |
|
|
|
y 0 1, |
z 0 4. |
z 2 y 5z, |
Выразим из первого уравнения z :
z 14 y 34 y .
Тогда
z 14 y 34 y .
Подставляя выражения для z и z во второе уравнение системы, получаем
y 8y 7 y 0 .
Общим решением этого уравнения является функция
y C1e x C2e 7 x .
Отсюда из равенства z 14 y 34 y имеем
z 12 C1e x C2e 7 x .
Удовлетворяя решение начальным условиям, находим
y 2e x 3e 7 x , z e x 3e 7 x . ▲
3
Рассмотрим физический смысл нормальной системы дифференциальных уравнений. Ограничимся случаем системы трех дифференциальных уравнений относитель-
но трех искомых функций x(t) , y(t) , |
z(t) , будем считать, что t |
– время. Тогда система |
||
(87) примет вид |
|
|
|
|
x f1 (t, x, y, z), |
|
|
||
|
|
|
||
|
f2 (t, x, y, z), |
|
|
|
y |
. |
(6) |
||
|
f3 (t, x, y, z). |
|||
|
|
|||
z |
|
|
||
решение этой системы есть некоторая кривая в пространстве с декартовой прямоугольной системой координат Oxyz . Пространство Oxyz называется фазовым пространст-
вом, а интегральная кривая – фазовой траекторией системы (92). Сама система (92)
называется динамической системой.
Динамическая система (92) определяет поле скоростей движущейся в пространстве точки в любой момент времени t . Решение динамической системы x x(t) ,
y y(t) , z z(t) – это уравнения движения точки: они определяют положение движу-
щейся точки в любой момент времени t . Начальные условия задают положение точки в начальный момент времени. Уравнения движения определяют также и траекторию движения, будучи уравнениями этой кривой в параметрической форме.
Динамическая система называется автономной (стационарной), если в правые части уравнений этой системы время t не входит явным образом. Если для автономной системы выполняются условия теоремы существования и единственности решения задачи Коши, то через каждую точку фазового пространства проходит только одна траектория, в отличие от неавтономной системы.
Автономные системы описывают установившиеся (стационарные) движения потока жидкости, газа, заряженных частиц и т.д., то есть те случаи, когда поле скоростей не изменяется с течением времени.
Понятия динамической системы, фазового пространства и фазовой траектории рассматривают и для общего случая нормальных систем вида (87).
Пример. Построить фазовые траектории системы
x y,y x.
В рассматриваемом примере фазовым пространством является плоскость Oxy переменных x, y . Исключая время t из системы уравнений, имеем
dx |
|
dy |
|
y |
dx |
|
y |
xdx ydy 0 . |
||||
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dt |
|
dt |
|
x |
|
|
|
|
|
|||
|
|
dy |
|
x |
|
|||||||
Отсюда интегрированием получаем равенство x2 y2 C2 , где C – произвольная постоянная. Это равенство определяет на плоскости Oxy концентрические окружности с центром в точке O 0, 0 . ▲
4

Нормальной линейной однородной системой n -го порядка называется система
вида: |
|
|
|
|
|
|
|
y |
a y a y |
|
a |
y |
|
, |
|
1 |
11 1 12 |
2 |
1n |
|
n |
|
|
|
a21 y1 a22 y2 |
a2n yn , |
|
||||
y2 |
|
||||||
................................................ |
(7) |
||||||
|
|
|
|
|
|
|
|
|
an1 y1 an2 y2 |
ann yn , |
|
||||
yn |
|
||||||
|
|
|
|
|
|
|
|||||||||||
где коэффициенты aij |
|
( i, j 1, n ) |
могут быть функциями переменной |
x . Систему (7) |
|||||||||||||
записывают также в матричной форме |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Y A Y , |
|
|
|
|
|
(8) |
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y (x) |
|
|
|
y (x) |
|
a (x) |
a (x) |
a |
(x) |
||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
11 |
12 |
|
1n |
|
|
|
y2 (x) |
|
|
|
|
|
(x) |
|
a21(x) a22 (x) |
a2n |
(x) |
|||||||
|
|
y2 |
|
||||||||||||||
Y |
|
|
, |
Y |
|
|
|
, |
A |
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn (x) |
|
|
|
|
(x) |
|
an1 (x) an2 (x) |
ann (x) |
|||||||||
|
|
yn |
|
||||||||||||||
В области непрерывности коэффициентов aij ( i, j 1, n ) система (7) удовлетворяет условиям теоремы существования и единственности решения задачи Коши.
Фундаментальной системой решений системы (7) называется совокупность
произвольных n линейно независимых решений |
|
|
|
||||
|
(k ) |
(x) |
|
|
|
|
|
y1 |
|
|
|
|
|
||
y |
(k ) |
(x) |
|
|
|
|
|
|
|
|
|
|
|||
Yk (x) |
2 |
|
|
, |
k 1, n . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k ) |
(x) |
|
|
|
|
|
yn |
|
|
|
|
|
||
Если Yk (x) , k 1, n – фундаментальная система решений системы (7), то общее решение системы (7) имеет вид
n
Y (x) CkYk (x) ,
k 1
где C1, C2 , , Cn – произвольные постоянные.
5

В частном случае систем с постоянными коэффициентами, когда матрица A в правой части (8) не зависит от x , для отыскания фундаментальной системы решений
Yk (x) , k 1, n , могут быть использованы методы линейной алгебры.
Будем искать решение системы (8) в виде |
|
Y (x) X ( ) e x . |
(9) |
Подставляя (9) в (8), получаем |
|
(A E) X ( ) O , |
(10) |
где E – единичная матрица, O – нулевая матрица-столбец. Равенство (10) представляет собой систему линейных алгебраических уравнений, неизвестными которой являются элементы матрицы X ( ) . Из условия существования нетривиального решения однородной системы (10) получается уравнение
det(A E) 0 , |
(11) |
называемое характеристическим уравнением. Заметим, что корни характеристического уравнения (11) называются собственными значениями матрицы A , а ненулевые
матрицы-столбцы X ( ) , получаемые из решения системы (10), |
называются собствен- |
ными векторами матрицы A . |
|
Из уравнения (11) находятся различные корни 1 , 2 ,…, m и для всякого корня |
|
(с учетом его кратности) определяется соответствующее |
ему частное решение |
Y ( ) (x) . Тогда общее решение системы (8) имеет вид |
|
m |
|
Y (x) CkY ( k ) (x) . |
(12) |
k 1
При этом возможны следующие случаи.
1. – действительный корень кратности 1. Тогда
|
( ) |
|
x1 |
|
|
x |
( ) |
|
Y ( ) (x) X ( )e x |
2 |
e x , |
|
|
|
|
|
|
|
( ) |
|
xn |
|
|
где X ( ) – собственный вектор матрицы A , соответствующий собственному значению
.
6

2. – комплексный корень кратности 1. Тогда корнем характеристического уравнения (11) является также сопряженное с число . Вместо комплексных частных решений Y ( ) (x) и Y ( ) (x) следует взять действительные частные решения
Y1( ) (x) ReY ( ) (x) и Y2( ) (x) ImY ( ) (x) .
3.– корень кратности r 2 . Соответствующее этому корню решение системы
(8)ищется в виде
|
11 |
12 x 1r xr 1 |
|
|||||||
|
|
|
|
|
x |
|
xr 1 |
|
|
|
|
|
|
|
|
|
|||||
Y ( ) (x) |
|
21 |
|
22 |
|
2r |
|
|
e x , |
(13) |
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
n2 x nr x |
r 1 |
|
|
|||||
|
|
|
|
|||||||
коэффициенты которого ij ( i 1, n , j 1, r ) определяются из системы линейных урав-
нений, получающихся приравниванием коэффициентов при одинаковых степенях x в результате подстановки решения (13) в исходную систему (8).
Пример. Решить задачу Коши
|
|
|
|
|
|
y |
4 y |
y |
, |
|
|
|
|||
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3y1 2 y2 , |
|
|
|
|||
|
|
|
|
|
|
y2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 y1 3y2 4 y3 , |
|
|
||||
|
|
|
|
|
|
y3 |
|
|
|||||||
|
|
|
|
y1 (0) 6 , |
y2 (0) 6 , |
y3 (0) 24 . |
|
|
|||||||
Характеристическое уравнение для этой системы имеет вид |
|
|
|||||||||||||
|
|
4 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
det(A E) |
|
3 |
2 |
0 |
|
0 |
|
|
(4 )(2 )(4 ) 3(4 ) 0 |
|
|||||
|
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
||
|
(4 )[(2 )(4 ) 3] 0 |
|
(4 )[ 2 6 5] 0 |
|
|
||||||||||
Его корни 1 |
1, |
2 4 , 3 |
5 . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
( k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
Обозначим |
X ( k ) |
x |
( k ) |
собственный вектор соответствующий собственному |
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( k ) |
|
|
|
|
|
|
|
|
|
||
значению |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
( k 1,2,3). Согласно (10) компоненты векторов X ( k ) являются решением |
|||||||||||||||
|
|
|
|
|
|
(4 |
)( 1)( 5) 0 . |
|
|
||||||
k
системы
7
|
(4 k )x1( k ) x2( k ) 0, |
|
||
|
3x1( k ) (2 |
k )x2( k ) 0, |
|
|
|
|
|||
|
( k ) |
( k ) |
( k ) |
0. |
2x1 |
3x2 |
(4 k )x3 |
||
Для 1 1 имеем:
|
|
|
( 1 ) |
|
( 1 ) |
0, |
|
|
|
( 1 ) |
3c1 , |
|
|
|
3x1 |
x2 |
|
|
|
x1 |
|||||
|
|
3x1( 1 ) |
x2( 1 ) |
0, |
|
|
x2( 1 ) 9c1 , |
|||||
|
( 1 ) |
|
( 1 ) |
|
|
( 1 ) |
0, |
|
|
( 1 ) |
7c1 , |
|
2x1 |
|
3x2 |
3x3 |
|
x3 |
|||||||
где c1 – произвольная постоянная.
Для 2 4 имеем:
|
x2( 2 ) 0, |
|
|
3x( 2 ) |
2x( 2 ) |
0, |
|
|
1 |
2 |
|
2x( 2 ) |
3x( 2 ) |
0, |
|
|
1 |
2 |
|
где c2 – произвольная постоянная.
Для 3 5 имеем:
x( 2 )
1
x2( 2 )x3( 2 )
0,
0,
c2 ,
|
|
x1( 3 ) x2( 3 ) 0, |
|
|
|
3x1( 3 ) 3x2( 3 ) 0, |
|
|
|
||
2x( 3 ) 3x( 3 ) |
x( 3 ) 0, |
||
|
1 |
2 |
3 |
где c3 – произвольная постоянная.
x( 3 )
1
x2( 3 )x3( 3 )
c3 ,
c3 ,
5c3 ,
Полагая c1 1 , |
c2 1, |
c3 1 |
частные решения соответствующие k |
( k 1,2,3) |
||||||
имеют вид: |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y ( 1 ) (x) |
9 |
ex , |
Y ( 2 ) (x) |
0 |
e4 x , |
Y ( 3 ) (x) |
1 |
e5 x . |
|
|
|
|
7 |
|
|
1 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||
Отсюда общее решение системы в соответствии с (12) имеет вид
|
|
3 |
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Y (x) C1 |
|
9 |
ex C2 |
|
0 |
e4 x C3 |
|
1 |
e5 x . |
|
|
7 |
|
|
1 |
|
|
5 |
|
|
|
|
|
|
|
|
8
Для нахождения частного решения константы C1 , C2 , C3 определяем из систе-
мы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
3 |
|
|
0 |
|
|
|
1 |
|
|
3C1 C3 |
|
|
|
|
3C1 C3 |
6, |
|||||||
|
6 |
|
C1 |
|
9 |
|
C2 |
|
C3 |
|
|
9C1 C3 |
|
|
|
|
9C1 C3 |
6, |
|||||||||
Y (0) |
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
||||||||||||||
|
24 |
|
|
|
7 |
|
|
|
1 |
|
|
|
5 |
|
|
7C C |
2 |
5C |
|
|
7C |
C |
2 |
5C |
3 |
24, |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
1 |
|
|
|
|||||||
откуда C1 1, C2 2 , C3 3 . Окончательно для искомого частного решения получаем
|
|
|
3 |
|
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y (x) |
9 |
ex |
0 |
e4 x |
3 |
e5 x |
|||
|
|
|
7 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
||
Или |
|
|
|
|
|
|
|
|
|
|
y (x) 3ex 3e5x , |
y |
(x) 9ex 3e5x , |
y (x) 7ex 2e4 x 15e5x . ▲ |
|||||||
1 |
2 |
|
|
|
|
|
|
3 |
|
|
9
Численные методы решения обыкновенных дифференциальных уравнений
Решения многих дифференциальных уравнений не выражаются в элементарных функциях. В этих случаях пользуются приближенными методами интегрирования дифференциальных уравнений.
1. Метод Эйлера. Пусть требуется решить задачу Коши: найти решение дифференциального уравнения
|
y f (x, y) , |
(1) |
удовлетворяющее начальному условию y(x0 ) y0 . |
|
|
При численном решении уравнения (1) задача ставится так: |
в точках |
|
x0 , x1 , x2 ,…, xn |
найти приближенное значение yk для точного решения y(xk ) . Разность |
|
xk xk xk 1 |
называется шагом сетки. Во многих случаях величину xk |
принимают |
постоянной xk h const , тогда
xk x0 kh ( k 0,1,2,...,n ).
Заметим, что шаг сетки h задают по заданной предельной абсолютной погрешности с помощью неравенства h2 .
Метод Эйлера основан на непосредственной замене производной разностным
отношением по приближенной |
формуле |
y |
f (x, y) , где |
y y(x h) y(x) , |
|
|
x |
|
|
x (x h) x h . |
|
|
|
|
Приближенное значение yk |
в точке xk |
x0 |
kh вычисляется по формуле |
|
yk 1 yk |
hf (xk , yk ) ( k 0,1,2,...,n ). |
|
||
2. Метод Рунге-Кутта. Рассмотрим задачу нахождения |
частного решения |
|||
y y(x) , z z(x) ,… нормальной системы дифференциальных уравнений |
||||
|
y f (x, y, z,...), |
|
||
|
|
|
|
(2) |
|
z g(x, y, z,...), |
|||
|
|
|
|
|
|
............... |
|
||
удовлетворяющего заданным начальным условиям |
|
|||
|
y(x0 ) y0 , z(x0 ) z0 ,… |
(3) |
||
Заметим, что поскольку любое дифференциальное уравнение n -го порядка можно свести к нормальной системе n дифференциальных уравнений, то данный метод применим и для приближенного решения дифференциальных уравнений высшего порядка.
10
