§ 7. Формула полной вероятности, формула

БЕЙЕСА).

Пусть имеется полная группа несовместных событий - гипо- тез - , для которых известны их вероятности. Тогда, по следствию 1 из теоремы о сложении вероятностей, сумма их вероятностей равна 1, т.е..

Пусть некоторое интересующее нас событие может прои -зойти или не произойти в случае выполнения одной из гипотези известны условные вероятности появления событияпри выполнении каждой из гипотез:. Тогда вероятность событияопределяется по формуле:. (1)

Эта формула называется формулой полной вероятности.

В самом деле, событие можно представить следующим образом:. Так как события

несовместны, то входящие в событие слагаемые также несовместны, т.е.. По аксиоме умножения вероятностей,и тогда:. Получили нужную формулу.

Пример 1. Три станка – автомата, производительности кото -рых относятся как 3 : 2 : 5 штампуют одинаковые детали. 80% деталей, изготовленных 1 – м станком, 90%, изготовленных 2 – м станком, и 70%, изготовленных 3 – м станком, являются стан –дартными. Все изготовленные детали хранятся в одном ящике. Найти вероятность того, что взятая наугад деталь окажется стандартной.

Событие - «даталь стандартная» зависит от событий(т.е. от того, каким станком была изготовлена детпль). Вероятности этих событий, учитывая производитель- ности станков – автоматов, равны, соответственно,

Условные вероятности появления события определяются процентами стандартных деталей для каждого станка, т.е.

Тогда, по формуле полной вероятности (1),

Пример 2. Пусть в первой урне находится 8 белых и 12 синих шаров, во второй урне - 5 белых и 3 синих шара. Из первой урны произвольным образом извлекаются 2 шара и перекладываются во вторую урну. Затем из второй урны из- влекается один шар. Найти вероятность того, что извлечённый шар белый (событие ).

Событие зависит от того, какие шары были добавлены во вторую урну, т.е. от событий- «два белых шара»,- «белый и синий шар», событие- «два синих шара». Най – дём вероятности этих событий:

Условные вероятности события по каждому из этих со -бытий равны, соответственно,

Тогда вероятность события равна

Замечание. Формула полной вероятности - это следствие теоремы сложения вероятностей и аксиомы умножения вероят- ностей.

Поставим теперь следующую задачу. Пусть имеется полная групппа несовместных событий - гипотез - , для которых известны их вероятности,. Пусть некоторое интересующее нас событиеможет произой- ти или не произойти в случае выполнения одной из этих ги -потез и известны условные вероятности появления событияпри выполнении каждой из гипотез:. По формуле пол- ной вероятности (1) мы можем найти вероятность события. Пустьсобытие произошло. Требуется определить долю участия каждой из гипотез в выполнении события , т.е. най- ти вероятности:. Эти вероятности можем найти по следующей формуле:

. (2)

Эта формула называется формулой Бейеса.

В самом деле, из аксиомы умножения вероятностей,

эта формула получается автоматически.

Пример 3. В условиях примера 1 этого параграфа, опреде – лить вероятность того, что выбранная стандартная деталь из -готовлена 1 – м станком.

По формуле (2),

Пример 4. Четыре машинистки в течение определённого времени печатают рукопись в 300 счтраниц. Первая из них напечатала 60 страниц, вторая - 80, страниц, третья - 110 страниц, четвёртая - 50 страниц. Вероятность сделать опе - чатку для первой машинистки равна 0,2, для второй - 0,3, для третьей - 0,1 и для четвёртой - 0,4. После сверки текста была обнаружена опечатка. Какая машинистка, вероятнее все -го сделала опечаику.

В условиях этой задачи: событие - опечатка в тексте, события- опечатка была сделанай машинисткой.

Тогда вероятность ошибки в рукописи:

Теперь, воспользуясь формулой Бейеса, оценим вероятности:

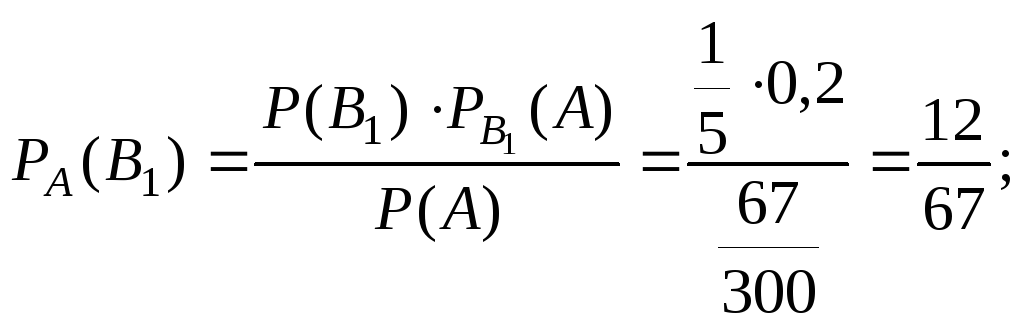
Таким образом, вероятнее всего опечатку сделала вторая машинистка.