§ 3 Частота события и её свойства,

Пусть произведена серия испытаний, в каждом из кото -рых может появиться или не появиться событие.

Частотой события в данной серии испытаний называ –ется отношение числаиспытаний, в которых появилось со- бытие, к общему числуиспытаний, т.е..

СВОЙСТВА ЧАСТОТЫ СОБЫТИЯ.

1. Частота случайного события неотрицательное число, не большее единицы, т.е.

.

Это свойство очевидно, так как всегда .

2. Частота достоверного события равна единице (так как).

3. Частота невозможного события равна нулю 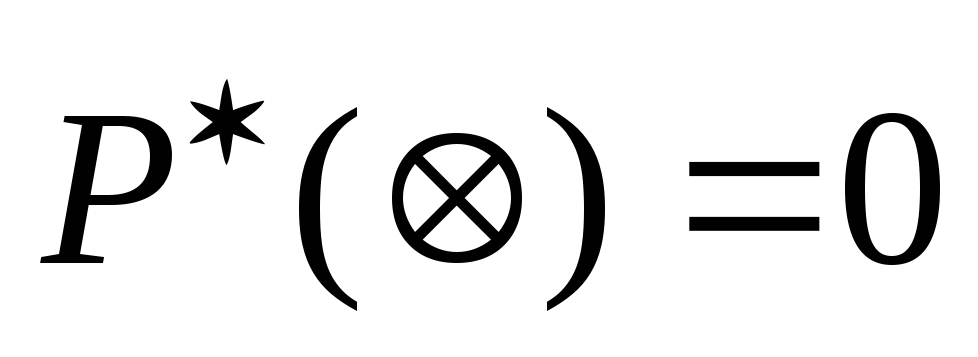. (так как в этом случае).

4. Частота суммы двух несовместных событий равна сум- ме частот этих событий, т.е.

.

В самом деле, если событие появилосьраз, а со- бытиераз виспытаниях, то, так как события не –совместны и невозможно их одновременное появление в дан- ных испытаниях, событиепоявитсяраз.

Тогда

.

Чтобы сформулировать следующее свойство, введём ещё одно понятие. Частота одного события, вычисленная при ус- ловии, что произошло другое событие, называется условной частотой и обозначается . Если событияисовместны, то можем сформулироватьсвойство ум- ножения частот.

5. Частота произведения двух событий равна произведе –

нию частоты одного из них на условную частоту другого

(1)

В самом деле, пусть в серии из испытаний событиепоявилосьраз, событие-раз, а вместе эти собы- тия появилисьраз. Тогда

Если мы подставим все эти частоты в формулу (1), то получим тождество :

.

Длительные наблюдения показали, что если в одинаковых условиях производятся опыты, в каждом из которых число ис -пытаний достаточно большое, то частота события проявляет свойство устойчивости: в различных опытах частота меня- ется мало (тем меньше, чем больше число испытаний в опыте) и колеблется относительно некоторого постоянного числа.

§ 4 Вероятность события.

Учитывая свойство устойчивости частоты события, можно ввести понятие вероятности события.

Определение. Вероятностью случайного события назы –вается постоянное число, около которого группируются часто- ты этого события по мере увеличения числа испытаний.

Это определение вероятности называется статистическим.

Положительное свойство этого определения заключается в том, что оно опирается на реальный эксперимент. Но в этом же кроется и его отрицательная сторона. Для надёжного опреде -ления вероятности, в смысле этого определения, необходимо произвести большое число опытов, что зачастую связано с большими материальными затратами, например, при проверке изделий на надёжность, которая приводит к разрушению изде- лия. Однако то, что каждое массовое случайное событие имеет свою вероятность, является фактом, подтверждаемым опытом, что и доказывает существование статистических закономернос- тей в природе.

Однако статистическое определение вероятности, как осно- ванное на экспериментальных данных, не даёт возможности заранее, до эксперимента, определить вероятность события, т.е. не является «рабочим определением».

Рассмотрим другое определение вероятности, которое на -зывается классическим. Это определение основано на понятии равновозможных несовместных событий (исходов данного опы -та, которые образуют полную группу, т.е. учтены все возмож -ные исходы данного опыта), т.е. шансов. Рассмотрение таких групп равновозможных событий можно свести к так называе -мой «схеме урн» (урна содержит одинаковые, неразличимые на ощупь шарики: разноцветные или занумерованные, которые из- влекаются произвольным образом). Например, испытание с подбрасыванием монеты можно сравнить с извлечением из ур- ны, содержащей два шара (белого и чёрного), шара опреде -лённого цвета. Опыт «подбрасывание игрального кубика» рав- носилен опыту «извлечение из урны, содержащей 6 занумеро- ванных шаров, шара с определённым номером» и т.п.

По отношению к каждому событию равновозможные исходы (шансы) делятся на благоприятные, при которых событие про- исходит, и, соответственно - неблагоприятные, при которых со- бытие не происходит. Например, при бросании игрального ку –бика, для события - «выпало чётное число» благоприятны- ми являются 3 шанса - выпали цыфры 2, 4, 6.

Определение. Вероятностью появления некоторого собы- тия называется отношение числа шансов, благоприятствующих данному событию, к общему числу равновозможных в данном опыте шансов. Такое определение вероятности называется классическим.

Другими словами , где- общее число равно- возможных исходов, а- число благоприятных исходов.

Важным достоинством этого определения является то, что с его помощью вероятность события можно определить зара- нее, до опыта, и сделать соответствующие выводы.

Недостаток его заключается в том, что это определения можно применять только в случае равновозможных исходов опыта.

Рассмотрим несколько примеров.

1. Двоекратное подбрасывание монеты. Возможные исходы

«ГГ, ГЦ, ЦГ, ЦЦ» (Г – герб, Ц – цифра). Всего . Собы- тие- выпала хотя бы одна цифра. Тогда количество бла- гоприятных исходови вероятность события:

2. В урне находится 10 шаров, из которых 6 белых и 4

чёрных. Произвольным образом извлекаются 2 шара. Опреде- лить вероятность того, что оба шара белые (событие ).

Общее число исходов в данном случае

.

Число благоприятных исходов . Тогда вероятность события:.

3. Из цифр 1, 2, 3, 5 составляется 4 - х значное число.

Определить вероятность того, что полученнок число чётное (событие ). Общее число возможных исходов:

Число благоприятных исходов (так как пос- ледняя цифра 2 уже зафиксирована), Тогда

.

4. В коробке 20 шаров, из которых 7 красных, 8 синих и

5. зелёных. Случайным образом извлекаются 6 шаров. Найти

вероятность того, что среди отобранных шаров разноцветные шары будут поровну, т.е. по 2 (Событие ).

Общее число исходов

Число благоприятных исходов

Тогда .

При классическом определении вероятностей можно расс -матривать только конечные полные группы равновозможных событий. На практике же зачастую встречаются такие испы –тания, число возможных исходов в которых бесконечно. При- менить классическое определение в данном случае невозмож- но. Однако в этом случае можно воспользоваться так называ -емым геометрическим определением вероятности, которое также опирается на понятие равновозможности исходов данно- го опыта. Применяется этот метод в задачах, сводящихся к случайному «бросанию точки» на конечный участок прямой, плоскости или пространства. Можно ограничиться плоским слу- чаем, так как одномерный и трёхмерный случаи отличаются только тем, что вместо площади в них имеем дело с длиной отрезка или с объёмом.

Пусть на плоскости имеется некоторая область пло- щади, внутри которой произвольным образом располо –жена областьс площадью. В областьнаугад бро- сается точка. Считая равновозможными исходами данного опы-

та попадание в любую точку области , требуется опре- делить вероятность попадания этой точки в область. В та- ких условиях вероятоность попадания точки в какую – либо часть области пропорциональна площади этой части и не за- висит от её формы и места расположения, т.е. вероятность можно найти по формуле:.

Рассмотрим несколько примеров.

1. Пусть даны две концентрические окружности радиусов

и , соответственно, Точка бросается в круг большего ра- диуса. Найти вероятность того, что она попадёт в кольцо, зак- лючённое между окружностями Так как площадь,

площадь , то искомая вероятность равна

.

2. На отрезок числовой оси, длиной 5 см, произволь-

ным образом ставятся две точки и(). Найти вероятность того, что из полученных отрезковможно построить треугольник.

05

Чтобы из данных от- резков можно было построить треугольник, должны быть вы -полнены следующие условия:

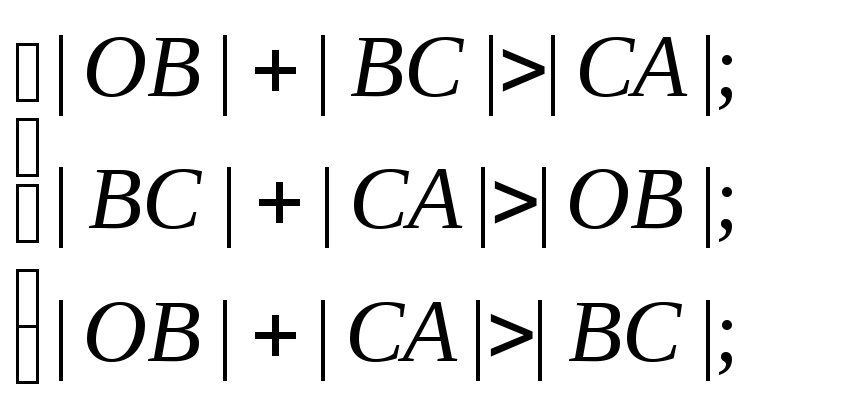или

Кроме того, в данных условиях, .

Из второй системы получаем условия, которые необходимы по условию задачи:

= .

Это геометрическа

5 иллюстрация данной

задачи.

2,5

0 2,5 5

Область - это квадрат стороной 5 см., область- это выделенная часть квадрата. Её площадь составляет вось- мую часть площади квадрата. Поэтому искомая вероятность.

И таких задач, которые сводятся к вычислению геометри- ческих вероятностей существует достаточно много.