§ 6. Функция одного случайного аргумента её

РАСПРЕДЕЛЕНИЕ И МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ

Если каждому значению случайной величины соответ- ствует одно из возможных значений случайной величины, тоназывают функцией случайного аргумента:

1. Пусть - дискретная случайная величина.

а) Если различным значениям случайной величины отве- чают различные значения случайной величины, то вероят -ности соответствующих значенийиравны между собой.

Пример 1. Дискретная случайная величина задана рядом распределения:

	- 2	-1	0	1	2
	0,2	0,1	0,1	0,3	0,3

Тогда закон распределения функции задаётся рядом:

	- 9	-2	-1	0	7
	0,2	0,1	0,1	0,3	0,3

б) Если различным значениям отвечают значения случай- ной величины, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений.

Пример 2. Пусть случайная величина задана тем же рядом распределения:

	- 2	-1	0	1	2
	0,2	0,1	0,1	0,3	0,3

Тогда ряд распределения случайной величины имеет вид:

	0	1	4
	0,1	0,4	0,5

(при, поэтому складываем соответствующие вероятности 0,1+0,3=0,4;при, поэтому скла- дываем вероятности 0,2+0,3=0,5).

2. Пусть теперь - непрерывная случайная величина,

заданная плотностью распределения . Пусть функция- дифференцируемая и сторого монотонная, т.е. имеет дифференцируемую обратную функцию. Тог -да плотность распределения случайной величиныгаходится с помощью равенства:

.

Пример 3. Пусть случайная величина распределена по закону Коши

.

Найти плотность распределения случайной величины .

Обратная функция . Эта функция строго монотонна и дифференцируема

.

. Тогда плотность распределения случай- ной величины имеет вид:

.

Если функция в интервале возможных значенийне монотонна, то стоит разбить этот интервал на интер- валы, в каждом из которых функцияявляется мо- нотонной, найтидля каждого из интервалов монотон –ности и затем представитьв виде суммы:

Пример 4. Задана плотность распределения нормально распределённой случайной величины :

Найти плотность распределения случайной величины.

Из уравнения . Так как на промежеткефункцияне монотонна, то обратная функция состоит из двух частей. На промежутке,

На промежутке

Тогда

, .

Тогда

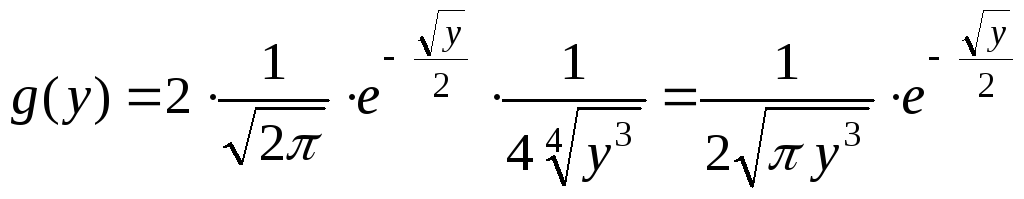
и вне этого интервала.

3. Пусть - дискретная случайная величина с возмож -

ными значениями , вероятности которых равны соответственно:. Функциятакже дискретная случайная величина, причём свои возможные зна- ченияона принимает с теми же ве- роятностями. Тогда её математическое ожи- дание вычисляется по формуле:

.

Пример 5 Пусть дискретная случайная величина задана рядом распределения:

	- 2	-1	0	1	2
	0,2	0,1	0,1	0,3	0,3

Найти математическое ожидание случайной величины

. Это также дискретная случайная величина с рядом распределения:

	- 10	- 3	0	-1	- 6
	0,2	0,1	0,1	0,3	0,3

Тогда

6.4. Пусть теперь - непрерывная случайная величина с плотностью распределения . Чтобы найти математичес -кое ожидание функции, можно воспользоваться двумя способами:

а) сначала найти плотность распределения данной функции и непосредственно применить формулу для вычисле -ния математического ожидания

;

б) если отыскание плотности вызывает затруднение, то математическое ожидание можно найти по формуле

.

Пример 6. Пусть задана плотность распределения случайной величины

Найти математическое ожидание функции

В этом примере математическое ожидание проще найти ис- пользуя способ б). Так как вне промежутка, то