МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Г.И. НОСОВА

Л.А. Изосова, А.В. Изосов

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И

ТЕОРИИ ВЕРОЯТНОСТЕЙ

Учебное пособие

(для студентов всех специальностей)

Утверждено Редакционно – издательским советом университета

в качестве учебного пособия

МАГНИТОГОРСК

2008

УДК 519.2

Изосова Л.А., Изосов А.В.

Элементы комбинаторики и теории вероятностей. Учеб. пособие. - Магнитогорск: МГТУ, 2008. – 112 с.

Изложены основные понятия комбинаторики, необходимые в курсе теории вероятностей. Основной материал по случайным событиям и случайным величинам приведён с достаточными обоснованиями и снабжён большим количеством примеров в соответствии с программой курса математики.

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.

Комбинаторный анализ занимается изучением объектов не – которого конечного множества и их свойств. Этими объектами могут быть подмножества множес -тва, подмножества из множествас повторяющимися элементами, упорядоченные подмножества множестваи т.п.

Комбинаторный анализ является разделом дискретной ма -тематики, истоки которой уходят в глубокую древность. В на- стоящее время интерес к нему значительно усилился. Бла – годаря этому, комбинаторный анализ превратился в достаточ- но развитую ветвь математики, которая непрерывно разраста- ется. Это затрудняет задачу очертить круг объектов и их свойств, которые принадлежат этому разделу. Но нас инте- ресуют более прозаические вопросы, а именно те вопросы, которые имеют непосредственное отношение к теории веро -ятностей, т.е. связанные с вычислением количеств появлений тех или иных событий в сериях некоторых испытаний.

При выборе элементов изразличных элементов принято говорить, что они образуютсоединение из эле –ментов по

В зависимости от того, имеет ли значение порядок эле -ментов в соединении или нет, а также от того, входят в со- единение все элементов или только часть их, различают три вида соединений.

ВИДЫ СОЕДИНЕНИЙ:

1. Соединения, отличающиеся друг от друга составом эле -ментов или их порядком, каждое из которых содержит элементов, взятых изразличных элементов, назы- ваетсяразмещением из элементов по

Например, напишем все размещения из элементов по два:

.

2. Соединения, каждое из которых содержит 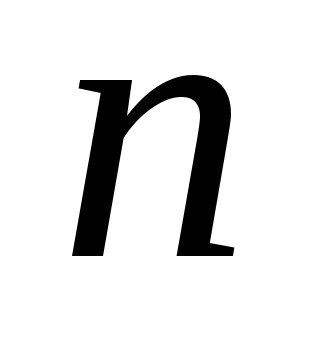различных

элементов, взятых в определённом порядке, называются пере- становками из элементов.

Например, напишем все перестановки из элементов :

3. Соединения, отличающиеся друг от друга по крайней ме- ре одним элементом, каждое из которых содержит элемен- тов, взятых изразличных элементов, называютсясочета – ниями (комбинациями или выборками) из элементов по

Например, напишем все сочетания из элементов по три элемента:

Задача о числе размещений. Сколькими способами можно выбрать и разместить по различным местамизраз- ных предметов (объектов) ? Количество всех таких способов принято обозначать(число размещений изпо).

Ясно, что на одно место можно поместить любой из предметов; таким образом:

().

Если одно место занято некоторым предметом, то на дру- гое место можно поместить любой из оставшихся, по- этому:

.

Продолжая аналогичные рассуждения, окончательно получим:

.

Рассмотрим несколько примеров.

Пример 1. Упростить выражение:

.

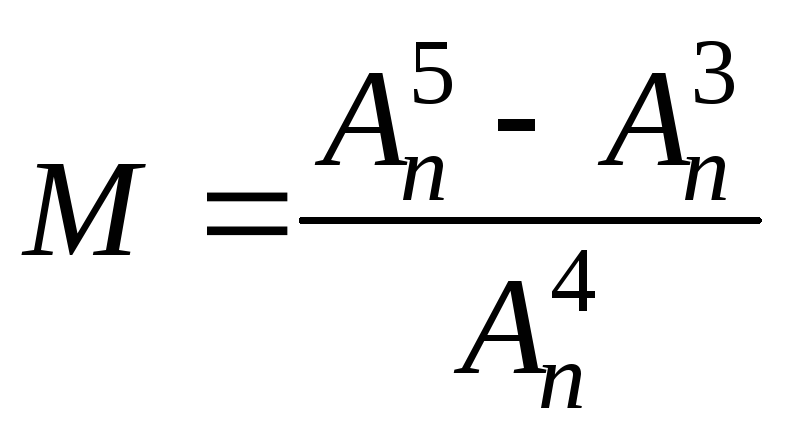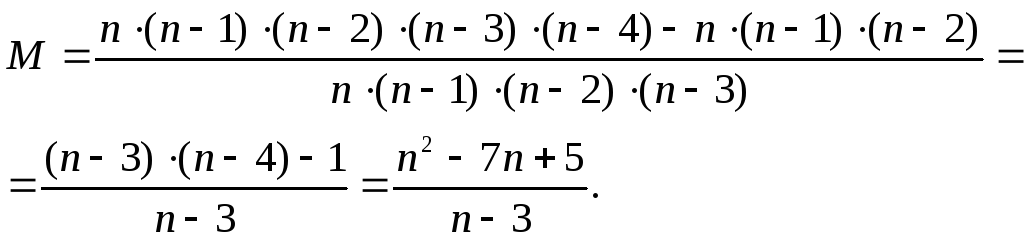
Пример 2. Пусть на плоскости заданы 8 точек. Сколько различных векторов можно построить по этим точкам.

Вектор соединяет две точки, причём важно, какая точка начальная, а какая конечная. Поэтому задача сводится к вычислению числу размещений . Применяем соответст -вующую формулу:

Пример 3. Сколько различных трёхзначных чисел можно составить из цифр: 0, 1, 4, 6, 7, 9.

Число различных размещений из 6 элементов по 3 равно:

Однако цифра 0 на первом месте не является значимой, поэ- тому из общего числа размещений нужно удалить комбинации, в которых 0 стоит на первом месте, т.е.

Окончательно

Пример 4. В соревновании по баскетболу университета при- нимают участие 7 команд, представляющих разные факульте - ты. Сколькими способами могут быть распределены призовые места (1 – е, 2 – е и 3 – е) между этими командами ?

В этой задаче опять важен порядок, поэтому опять приме -няем формулу:

Задача о числе перестановок. Сколькими способами можно переставить различных элементов, расположенных наразличных местах? Количество такихперестановок обозна -чается .

Эта задача сводится к нахождению числа размещений элементов намест, т.е. случай. Учитывая, что, по определению,0!=1, получаем:

Пример 5. Сколькими способами можно расставить на пол- ке 6 книг различных авторов ?

Пример 6. Русть 7 занумерованных шариков произвольным образом бросают в решётку с 7 – ю ячейками. Сколькими спо -собами шарики могут распределиться по ячейкам, при условии,

что каждый шарик попадает в какую – то одну ячейку.

Задача сводится к вычислению числа перестановок:

Задача о числе сочетаний. Сколькими способами можно вы- брать изразличных предметов. Количество всех таких способов принято обозначать(число сочетаний изпо, без учёта порядка элементов).

Выбрать изразличных предметов можноспосо-бами, а возможностей упорядочить предметов из данного соче- тания -. Поэтому имеетсявозможностей выбрать и разместить поразным местамизразных предметов, т.е.тогда

Легко доказать следующие свойства числа сочетаний:

1. 2.3.

Приведём несколько прмеров применения формулы числа сочетаний из поэлементов

Пример 7. 12 человек играют в городки. Сколькими спо -собами они могут выбрать команду из 4 человек на сорев –нование ?

Пример 8. В выпуклом семиугольнике проведены всевоз -можные диагонали, причём никакие три из них не пересека- ются в одной точке (т.е. не выходят из одной вершины). Сколько точек пересечения имеют данные диагонали ?

Каждой точке пересечения диагоналей в этом случае соот – ветствует 4 вершины семиугольника, а каждой четвёрке вер -шин соответствует одна точка пересечения диагоналей. Поэто- му число точек пересечения диагоналей семиугольника равно числу способов выбрать четыре вершины из семи, т.е.

Пример 9. В розыгрыше первенства по футболу участвует 16 команд, причём любые две команды играют между собой только один раз. Сколько всего произведено игр ?

Поставленная задача - задача о числе выборок из 16 по 2. Поэтому:

Пример 10. Из 2 математиков и 10 экономистов необходимо составить комиссию в составе 8 человек. Сколькими способа -ми может быть составлена комиссия, если в неё должен вхо -дить хотя бы один математик ?

Самый простой способ найти количество способов составле- ния таких комиссий - это от общего числа вариантов комис -сий, составленных из 12 человек по 8, отнять количество ко -миссий, в которых нет ни одного математика, т.е.

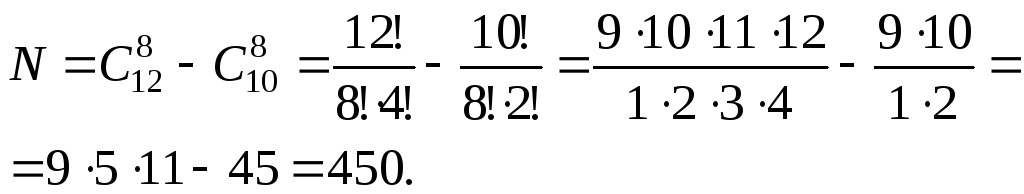
Пример 11. Из большого букета, содержащего 12 роз, 9 хризантем, 15 гвоздик и 7 герберов случайным образом наби- рают букет из 15 цветов. Сколькими способоми можно набрать

такой букет, чтобы в нём было 3 розы, 5 хризантем, 5 гвоз -дик и 2 гербера.

Общее количество цветов в набираемом букете - , причём,

Общее количество всех цветов - причём,

Тогда число вариантов находится следующим образом:

До сих пор мы рассматривали соединения, в каждое из ко- торых любой из различных элементов входит один раз. По- мимо этого можно рассматривать соединения, в которые лю -бой изэлементов может входить более одного раза, т.е.соединения с повторениями. В задачах с повторениями не имеет значения, что больше или.

Задача о числе размещений с повторениями. Сколькими способами можно разместить на местэлементов, для каждого из которых естьразличных вариантов ? Количество таких размещений обозначаетсяи равно:

Пример 12. Пусть каждый телефонный номер состоит из 6 цифр. Сколько существует телефонных номенов, содержащих только цифры: 2, 4, 6, 8 .

В этом примере Тогда

Пример 13. В секретном замке на общей оси находятся че- тыре диска, каждый из которых разделён на 5 секторов, на ко- торых записаны цифры от 0 до 4. Сколько возможно различ -ных кодовых вариантов ?

Здесь Тогда

Пример 14. Сколькими способами можно разместить 7 пасса- жиров в 3 вагона ?

В данном случае, и, следовательно,

Задача о числе перестановок с повторениями. Сколькими способами можно переставить различных предметовраз- ных типов, количества каждого из которых равны, соответст -венно( причём) ?

Если учесть, что при перестановке элементов оного типа ничего не изменяется, т.е. получаем выражения того же вида, то перестановок с повторениями будет меньше, чем обычных перестановок, а именно, для определения количества таких пе- рестановок необходимо общее число перестановок разделить на число перестановок среди одинаковых элементов, т.е.

Пример 15. Сколько различных перестановок можно выпол -нить в слове «фантастика» ?

Здесь ф - 1 (), а - 3 (), н, с, и, к - 1 (), т - 2 (). Тогда

Пример 16. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по две, три и четыре книги в каждой бандероли?

Пример 17. Сколькими способами можно распределить де -сять молодых специалистов по трём цехам комбината в кото- рых требуется 5, 3 и 2 специалиста, соответственно ?

Сочетаниями из предметов пос повторениями на -зываются соединения, содержащие предметов (без учёта порядка следования), причём каждый предмет может входить в соединение некоторое число раз, не больше.

Задача о числе сочетаний с повторениями. Если имеется по одинаковых предметов каждого изразличных типов, то сколькими способами можно выбратьиз этихпредметов?

Число таких сочетаний с повторениями обозначается и вычисляется по формуле:

.

Рассмотрим несколько прмеров:

Пример 18. В кондитерской имеется 10 сортов пирожных. Сколькими способами можно купить 4 пирожных?

Тогда

Пример 19. В почтовом отделении имеется в наличии 5 видов открыток «С праздником 8 Марта». Сколькими спосо- бами можно купить 10 поздравительных открыток ?

В этом примере тогда:

Пример 20. Сколькими способами можно выбрать 5 монет из 5 - ти двух рублёвых монет и 5 - ти одно рублёвых монет?

Это задача о сочетаниях из двух по пяти с повторениями.

Замечание. Как и для случая размещений с повторениями, при вычислении числа сочетаний с повторениями, не имеет значения, что больше или.

Итак, мы рассмотрели основные комбинаторные задачи, которые необходимы нам при вычислении вероятностей событий.

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

СЛУЧАЙНЫЕ СОБЫТИЯ

§ 1 Предмет теории вероятностей.

Одним из основных понятий, которыми оперирует теория

вероятностей, является событие.

Событием в теории вероятностей называется любой резуль- тат, который может произойти в итоге некоторого опыта (испы- тания).

Все наблюдаемые нами события могут быть подразделены на три вида: достоверные, невозможные и случайные.

Достоверными называют события, которые обязательно про- изойдут при выполнении определённой совокупности условий.

Например, достоверным является событие: «при бросании игрального кубика выпала цифра не больше 6».

Невозможным называется событие, которое заведомо не произойдёт при выполнении определённых условий.

Например, невозможным является событие: «при бросании игрального кубика выпала цифра 8».

Случайным (или возможным) называется событие, которое может произойти или не произойти в данных условиях.

Например, в том же опыте, случайным является событие: «при бросании игральньго кубика выпала цифра 3».

Каждое случайное событие зависит от действия многих слу- чайных причин, причём невозможно учесть влияние этих причин на результат (их много и законы их действия непредсказуе -мы). Поэтому теория вероятностей не ставит перед собой за- дачу предсказать наперёд, произойдёт ли данное конкретное событие или нет. Но, если рассматриваются случайные собы- тия, которые могут многократно наблюдаться в одних и тех же условиях (например, многократное подбрасывание монеты), т.е., если речь идёт о массовых однородных событиях, то оказы -вается такие однородные события, независимо от их конкрет- ной природы, подчинены определённым закономерностям, а именно вероятностным закономерностям.

Итак, предметом теории вероятностей является изу -чение вероятностных закономерностей массовых одно -родных случайных событий.

Знание закономерностей, которым подчинены массовые од- нородные случайные события позволяет предвидеть, как эти события будут проистекать. Можно, например, предсказать с небольшой погрешностью число появлений «герба», если моне- та будет подброшена большое число раз.

Методы теории вероятностей широко применяются в раз -личных отраслях науки и техники (теоретическая физика, тео- рия надёжности, теория стрельбы, теория ошибок наблюдений, общая теория связи, геодезия, астрономия и т.д.)

Теория вероятностей служит также базой математической и прикладной статистики, которые, в свою очередь, используются при планировании и организации производства, при анализе технологических процессов, при контроле качества производст -ва и т.п.

Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и др. в 16 -17 веке). Следующий этап развития теории вероятностей связан с именем Бернулли (1654 – 1705) Доказанная им теоре- ма «Закон больших чисел» была первым теоретическим обос- нованием накопленных ранее фактов. Дальнейшим успехам те- ория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др. Наиболее плодотворный период развития теории вероят- ностей связан с известными именами русских математиков, та- ких как Чебышев, Ляпунов, Марков (19 – 20 век). В этот пери -од теория вероятностей становится строгой математической на- укой.