2. Магнитные цепи

2.1. Основные понятия

В современных электронных устройствах для увеличения магнитного потока в определенной части пространства используют ферромагнитные материалы. Устройства или их совокупность, содержащие ферромагнитные материалы, предназначенные для создания с помощью намагничивающей силы магнитного потока, называют магнитной цепью.

Магнитное поле характеризуется вектором магнитной индукции . По принципу суперпозиции внутри вещества, магнитное поле складывается из внешнего поля и наведенного им (по гипотезе Ампера):

, (31)

где - магнитная индукция внутри вещества;

- магнитная индукция внешнего поля в вакууме;

- магнитная индукция наведенного поля, определяется магнитными свойствами вещества.

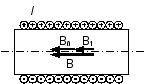Если внешнее поле создается бесконечной катушкой, витки которой навиты вплотную друг к другу, то согласно закону Био-Савара:

, (32)

Рис. 22. Катушка с сердечником

где - алгебраическая сумма токов, пронизывающие поверхность, ограниченные контуром;

- циркуляция вектора магнитной индукции по замкнутому контору;

- магнитная постоянна [Гн/м].

Магнитное поле бесконечной катушки однородное, поэтому выражение (32) можно записать:

, (33)

где – число витков катушки, уложенных на участке длинной;

- величина тока в катушке;

- намагничивающий ток.

Введем понятие вектора напряженности магнитного поля , который не зависит от свойств среды (вещества), и определяется только токами в проводах:

. (34)

Намагниченность вещества является результатом действия внешнего магнитного поля:

, (35)

где - магнитная восприимчивость вещества.

Учитывая (35), выражение (31) можно переписать в виде:

, (36)

где − относительная магнитная проницаемость ;

−абсолютная магнитная проницаемость.

Магнитная проницаемость зависит от строения вещества и в общем случае изменяется с изменением, т.е. зависимостьявляется нелинейной. Эта зависимость не имеет точного аналитического выражения и поэтому ее изображают для каждого ферромагнитного материала в виде кривой намагничивания, определяемой опытным путем.

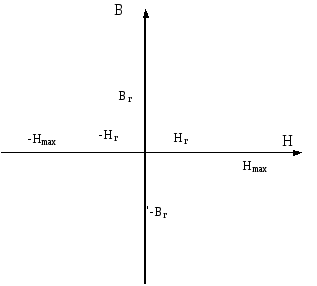
Рис. 23. Кривая намагничивания ферромагнитного материала

Если изменять отдо, то после нескольких циклов перемагничивания можно получить замкнутую петлю гистерезиса (рис.23). На этом рисунке– остаточная индукция,– коэрцитивная сила. Основной кривой намагниченности называют геометрическое место вершин замкнутых симметричных петель гистерезиса, снятых при различных (см.рис.23 -пунктирная кривая).

2.2. Законы Ома и Кирхгофа для магнитных цепей

Между ЭДС и током электрической цепи, и магнитным потоком с вызывающим этот поток током существует формальная аналогия.

Рассмотрим катушку, намотанную на замкнутый магнитный сердечник (рис.24.). Согласно закону полного тока:

. (37)

В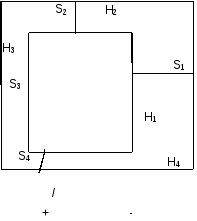ведем понятие магнитодвижущей силы(намагничивающей силы):

, (38)

и магнитных напряжений на участках цепи:

, (39)

где - магнитный поток;

- площадь поперечного сечения;

Рис. 24. Магнитная цепь - магнитное сопротивление.

С учетом введенных обозначений уравнение (37) можно записать:

. (38)

Последнее уравнение и выражает второй закон Кирхгофа для магнитных цепей.

Непрерывность магнитного потока, также как и непрерывность электрического тока определяет первый закон Кирхгофа для магнитных цепей:

. (39)

Алгебраическая сумма магнитных потоков в любом узле магнитной цепи равно нулю.

Д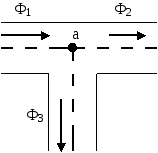ля узлаa магнитной цепи (рис.25) согласно первому закону Кирхгофа:

.

В таблице 6 сведены основные понятия и законы магнитных цепей.

Рис. 25. Узел магнитной цепи

Аналогия электрических и магнитных цепей Таблица 6

Электрическая цепь	Магнитная цепь
Электрический ток ,	Магнитный поток ,
Падение напряжения	Падение магнитного напряжения
Сопротивление
Сопротивление воздушного зазора
Первый закон Кирхгофа
Второй закон Кирхгофа

В заключении следует отметить, магнитная цепь из-за нелинейности кривых намагничивания (,) следует отнести к разделу нелинейных цепей.