1.2.5. Анализ разветвленных цепей

Расчет разветвленных цепей графическим способом рассмотрим на конкретном примере цепи на рис.14.а. ВАХ нелинейных элементов для упрощения графических построений приняты одинаковыми и приведены на рис. 6.14.б.

Рис.14. Расчет разветвленной цепи

а) схема цепи; б) ВАХ нелинейных элементов

Выбираем положительное направление токов в ветвях. Согласно второму закону Кирхгофа для напряжения можем записать:

; ;. (7)

Считая каждую ветвь активным двухполюсником, строим их ВАХ. (см. рис.15.). ВАХ двухполюсника получается сдвигом ВАХ резистивного элемента на соответствующую ЭДС. Предварительно ВАХ резистивного элемента необходимо отразить относительно оси абсцисс, т.к. в уравнения (7) они входят со знаком минус.

Согласно первому закону Кирхгофа имеем:

. (8)

Поэтому для нахождения точки установившегося режима строим вспомогательную кривую , для чего при одинаковых напряжениях складываем абсциссы кривыхи.

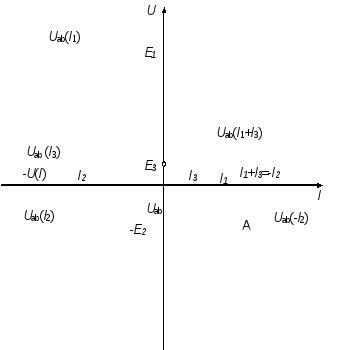
Рис.15. Построение для разветвленной цепи

Точка пересечения кривых и- точка А и определяет решение: напряжение, токи ветвей,,.

1.3. Аппроксимация характеристик нелинейных элементов

ВАХ реальных элементов обычно имеют сложный вид и их представляют в виде графиков или таблиц. В ряде случаев, например, при машинном анализе, такая форма представления ВАХ оказывается неудобной и их стремятся представить в виде аналитических зависимостей.

Замена сложных функций приближенными аналитическими выражениями называется аппроксимацией.

При выборе аппроксимирующих функций приходится решать две взаимоисключающих задачи: точность и простота аппроксимации. Чем выше требование к точности, тем, как правило, сложнее аппроксимирующая функция. Поэтому при решении каждой конкретной задачи необходимо идти на компромисс между точностью и сложностью аппроксимации.

Задача аппроксимации включает в себя две самостоятельные задачи: выбор функции и определение коэффициентов этой функции.

1.3.1. Выбор аппроксимирующей функции

Аппроксимирующая функция выбирается исходя из физических представлений о работе элементов, либо формально, основываясь на внешнем сходстве ВАХ с графическим изображением той или иной функции.

Для аппроксимации ВАХ используются как элементарные, так и различные трансцендентные функции, а также степенные, экспоненциальные, тригонометрические полиномы, кусочно-линейные функции.

Так как внешнее сходство с графическим изображением функции может оказаться обманчивым, перед тем, как перейти к определению значений коэффициентов, желательно проверить возможность ее применения, используя метод выравнивания.

Сущность метода заключается в том, что для проверки гипотезы о виде функциональной зависимости , заданной множеством значений (, ), переменные и заменяют некоторыми новыми переменными:

и , (9)

Замену выбирают таким образом, чтобы при сделанных допущениях о виде функции переменныеибыли связаны между собой линейной зависимостью:

. (10)

Если гипотеза о виде аппроксимирующей функции справедлива, то точки (,), при построении на координатной плоскости, должны располагаться на одной прямой. Рассмотрим вышесказанной на примере.

Пример 1. ВАХ нелинейного элемента задана в виде таблицы 1. Подобрать аппроксимирующую функцию.

Таблица 1

Табличные значения ВАХ элемента

x	0	0,2	0,4	0,6	0,8	1	1,2	1,4
y	0	0,268	0,759	1,394	2,146	3	3,94	4,969

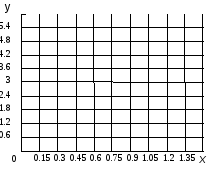
Решение. По данным таблицы 1 строим ВАХ (рис.16).

Анализируя построенную ВАХ, можно предположить, что она может быть аппроксимирована степенной функцией:

. (11)

Проверим эту гипотезу. Если прологарифмировать (11), получим:

Рис.16. ВАХ элемента . (12)

Обозначим через , через, подставляя значения (0,0) и (1,3), нетрудно определить коэффициентыи:

=1, =3.

Определившись с функциями:

, , (13)

рассчитываем значения новых переменных и сводим их в таблицу 2.

Проверка гипотезы вида ВАХ Таблица 2

xi	0	0,2	0,4	0,6	0,8	1	1,2	1,4
Xi		-4,82	-2,74	-1,53	-0,669	0	0,546	1,009
yi	0	0,268	0,759	1,394	2,146	3	3,94	4,969
Yi		-1,316	-0,275	0,332	0,763	1,098	1,371	1,603

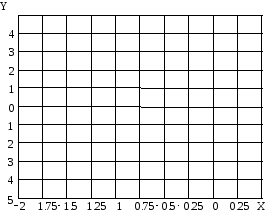
По данным таблицы 2 построена зависимость на рис.17.

Из рис.17 видно, что точки лежат на одной прямой, следовательно заданная ВАХ может быть аппроксимирована степенной функцией (11) при изменении от 0,2 до1,4.

Значение =0 и =0 выпадает из области определения выражений (13).

Рис.17. Проверка гипотезы вида

аппроксимирующей функции

В случае, если ВАХ аппроксимируется экспоненциальным полиномом вида:

, (14)

то проверить гипотезу можно введя подстановку:

, . (15)

Для определения коэффициента «с» выбирают два значения аргумента ,и определяют третий аргументи соответствующие им три значения функции,,, которые затем подставляют в уравнения:

. (16)

Для полинома второй степени:

, (17)

линейный вид можно получить подстановкой:

от . (18)

Если при проверке гипотезы о виде аппроксимирующей функции методом выравнивания окажется, что зависимость между вспомогательными переменными иимеет линейный характер только в определенном диапазоне то, следовательно, данная гипотеза справедлива только в соответствующем диапазоне изменения аргумента ВАХ нелинейного элемента.

Пример 2. ВАХ кремниевого диода задана таблично (см. таблицу 3).

Табличные значения ВАХ кремневого диода Таблица 3

x	U	0,2	0,4	0,6	0,8	1	1,2	1,4
y	I	0,033	0,077	0,138	0,2	0,3	0,5	0,85

Требуется проверить, можно ли аппроксимировать эту характеристику а) полиномом второй степени ;

б) экспоненциальным полиномом вида.

Решение. Подставляем в выражения (18) значения и рассчитываем значения вспомогательной переменной. Результат расчета сведен в таблицу 4.

Расчет вспомогательных переменных Таблица 4

xi	U	0,2	0,4	0,6	0,8	1	1,2	1,4
Xi		0,2	0,4	0,6	0,8	1	1,2	1,4
yi	I	0,033	0,077	0,138	0,2	0,3	0,5	0,85
Yi		0,033	0,044	0,061	0,062	0,1	0,2	0,35

П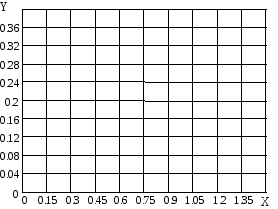о данным таблицы 4 строим зависимость(рис.18).

Как видно из рисунка, зависимость практически линейна при изменении от 0 до 1. Следовательно, в этой области рассматриваемая ВАХ может быть аппроксимирована полиномом второй степени.

Рис.18. Аппроксимация полиномом

Проверим можно ли аппроксимировать ВАХ диода с помощью экспоненциального полинома . Для определения константы с выберем три значения аргумента:

=0; =1,2;

==0,6.

Значения аргумента выбраны таким образом, чтобы значение функции можно было взять из таблицы. Если это невозможно сделать, то значение функции, соответствующее аргументу , можно брать приближенно. Например, если выбрать=0;=1;==0,5 , то значение функции=0;=0,3;0,095.

Для выбранных значений аргумента соответствующие значения функции =0;=0,5;=0,138.. Подставляя эти значения в уравнение (16), получим:

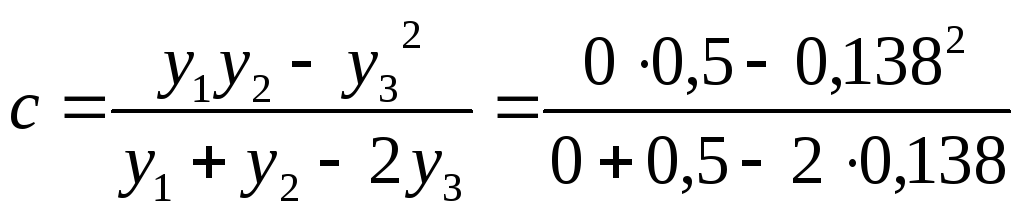=-0,085.

Рассчитаем значения вспомогательных переменных:

, .

Результаты расчетов сведены в таблицу 5

Расчет вспомогательных переменных Таблица 5

Xi =xi	0,2	0,4	0,6	0,8	1	1,2	1,4
yi	0,033	0,077	0,138	0,2	0,3	0,5	0,85
Yi	-2,465	-2,137	-2,048	-1,924	-1,687	-1,255	-0,832

На рис.19. построена зависимость.

Из вида которой следует, что зависимость может быть с достаточной степенью точности аппроксимирована экспоненциальной функцией.

Из приведенных примеров следует, что задача аппроксимации неоднозначная

Рис.19. Аппроксимация экспоненциальной функцией