1.2. Методы расчета резистивных нелинейных цепей постоянного тока

Электрическая цепь, содержащая хотя бы один нелинейный элемент, называется нелинейной.

Выделим два основных подхода, используемых для расчета и анализа нелинейных электрически цепей. Первый подход основан на графическом решении. Второй – аналитическое решение с использованием аппроксимирующих функций. Расчет нелинейных цепей обоими методами рассмотрен ниже на конкретных примерах.

1.2.1. Расчет цепей при последовательном соединении нелинейных элементов

Рассмотрим цепь, (рис.5) с двумя последовательно соединёнными нелинейными элементами, ВАХ которых приведены на рис.6. Требуется определить ток цепи и напряжение на элементах и при заданной э.д.с..

Рис.5. Цепь с последовательным Рис.6. ВАХ нелинейных

соединением нелинейных элементов элементов

Согласно второму закону Кирхгофа:

. (5)

Для решения уравнения (5) необходимо графическим путём найти сумму . Для этого, задаваясь рядом значений тока (,,и т.д., чем больше значений, тем точнее построим линию суммы), следует сложить ординаты ВАХ, как это сделано на рис.7.

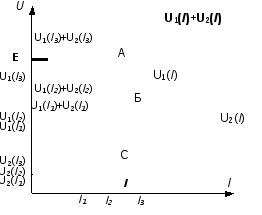
Рис.7. Пояснение к решению задачи.

Таким образом участок цепи с двумя элементами заменили одним нелинейным элементом, имеющим ВАХ . Построив горизонтальную линию , нетрудно определить ток , опустив перпендикуляр из точки пересечения А, и найти напряжение ина нелинейных элементах (определив ординаты точек Б и С).

Аналогичным образом можно решить задачу, если одно из нелинейных сопротивлений будет линейным, или цепь содержит не два нелинейных элемента, а несколько, последовательно соединённых.

1.2.2. Расчет цепей с параллельным соединением нелинейных элементов

Рассмотрим цепь, содержащую два параллельных нелинейных эле-мента (рис.8.а), ВАХ которых приведены на рис.8.б.

Рис.8. Расчет цепи при параллельном соединении элементов:

а) схема цепи; б) ВАХ элементов

Так как ==, а, то для нахождения результирующей ВАХ складываем абсциссы (токи) ВАХ,при одинаковых ординатах (напряжениях). Значение тока находим графическим путем с помощью результирующей ВАХ, как абсциссу пересечения с горизонтальной линией Е (точка А). Токи ветвей – точки С и Б соответственно.

1.2.3. Расчет цепей при смешанном соединении элементов

На рис.9 приведена цепь при смешанном соединении линейного сопротивления и двух нелинейныхиВАХ которых приведены на рис.10. Требуется определить установившиеся значения токов,,и напряжений на элементах при заданной ЭДС.

Рис.9. Цепь со смешанным соединением элементов

Сначала находим ВАХ параллельного участка путем сложения абсциссипри одинаковых напряжениях. Далее складывая ординаты характеристики, находим результирующую ВАХ всей цепи. Порядок построения показан на рис.10 стрелками.

Рис.10. Расчет цепи при смешанном соединении

Пересечения последней кривой с линией Е – точка А, позволяет определить ток и напряженияна параллельном участке. Пересечение линии напряженияс кривымииопределяет токи ветвей,.

1.2.4. Преобразование активных нелинейных двухполюсников

Рассмотрим цепь с последовательно соединенными нелинейным сопротивлением с Э.Д.С. постоянного тока(рис.11).

Рис. 11. Преобразование двухполюсников

а) активный двухполюсник с ЭДС; б,в) построение ВАХ двухполюсника

На основании второго закона Кирхгофа имеем:

, (6)

Из последнего уравнения следует, что ВАХ рассматриваемой цепи может быть получена суммированием ординат и ЭДС, т.е. путем смещения ВАХ навверх по ординате, если>0 и вниз если<0 (рис.11.б, в).

Рис. 12. Преобразование двухполюсников

а) активный двухполюсник с источником тока;

б,в) построение ВАХ двухполюсника

ВАХ активного двухполюсника, представляющее собой параллельное соединение нелинейного сопротивления и источника постоянного тока , получается путем смещения ВАХ нелинейного элемента вдоль оси тока на(рис.12.б,в).

Преобразованием двухполюсников пользуются не только для решения прямой задачи, но и для решения обратной задачи: заменить нелинейный двухполюсник, ВАХ которого не проходит через начало координат, нелинейным сопротивлением и идеализированным источником постоянного тока.

Рис.13. К решению обратной задачи

а) активный двухполюсник; б) ВАХ двухполюсника; в) ВАХ нелинейного сопротивления; г) схема замещения двухполюсника.

Покажем это на конкретном примере. Пусть активный двухполюсник (рис.13.а) имеет ВАХ, показанную на рис.13.б. Представим двухполюсник схемой замещения на рис.13.г. Из выражения (6) следует:

.

Для нелинейного сопротивления =0, получим, тогда можно записать:

.

ВАХ нелинейного сопротивления получается путем вычитания из ординат ВАХ двухполюсника. В итоге получаем ВАХ нелинейного сопротивленияна рис.13.в.