
- •Оглавление
- •Введение
- •Теплопроводность.
- •Основной закон теплопроводности.
- •1.2 Дифференциальное уравнение теплопроводности и условия однозначности.
- •1.2.1 Дифференциальное уравнение.
- •1.2.2 Условия однозначности.
- •1.3 Теплопроводность при стационарном режиме.
- •1.3.1.Теплопроводность плоской однослойной стенки.
- •1.3.2. Теплопроводность многослойной стенки.
- •1.4 Теплопроводность цилиндрической стенки.
- •1.4.1 Теплопроводность однослойной цилиндрической стенки.
- •1.4.2 Теплопроводность многослойной цилиндрической стенки.
- •1.5. Теплопроводность тел неправильной формы.
- •1.6. Нестационарная теплопроводность.
- •1.6.1 Общие положения. Описание процесса.
- •1.6.2 Решение задач нестационарной теплопроводности.
- •1.6.3. Охлаждение тел конечных размеров.
- •1.6.4 Зависимость процесса охлаждения от формы и размеров тела.
- •2. Теплопередача при стационарных условиях и граничных условиях 3 рода.
- •2.1 Теплопередача через плоскую стенку.
- •2.1.1 Теплопередача через однослойную стенку.
- •2.1.2 Теплопередача через многослойную стенку.
- •2.2 Теплопередача через цилиндрическую стенку при граничных условиях 3-го рода.
- •2.2.1 Теплопередача через однослойную цилиндрическую стенку.
- •2.2.2 Теплопередача через многослойную цилиндрическую стенку.
- •2.2.3 Теплопередача через шаровую стенку.
- •2.3. Интенсификация теплопередачи.
- •2.4. Критический диаметр изоляции.
- •3. Конвективный теплообмен.
- •3.1Основные понятия и определения.
- •3.2. Дифференциальные уравнения конвективного теплообмена.
- •3.3.Основы теории подобия.
- •Условия подобия физических процессов.
- •3.4. Теплоотдача при вынужденном продольным омывании плоской поверхности
- •3.4.1. Расчет теплоотдачи при ламинарном гидродинамическом пограничном слое.
- •3.4.2. Зависимость теплоотдачи от изменения температуры по ее длине.
- •3.4.3. Влияние на теплоотдачу необогреваемого начального участка
- •3.4.4. Теплоотдача при турбулентном пограничном слое
- •3.5. Теплоотдача при вынужденном течении жидкости в трубах
- •3.5.1. Теплоотдача при ламинарном режиме движения жидкости.
- •3.5.2. Теплоотдача при турбулентном режиме движения жидкости в трубах.
- •3.5.3. Теплоотдача при переходном режиме
- •3.5.4. Теплоотдача в трубах некруглого поперечного сечения.
- •3.5.5 Теплоотдача в изогнутых трубах
- •3.5.6. Теплоотдача в шероховатых трубах
- •3.6 Теплоотдача при вынужденном поперечном омывании труб и пучков труб.
- •3.61.Теплоотдача при поперечном омывании одиночной круглой трубы.
- •3.6.2 Теплоотдача при поперечном омывании пучков труб.
- •4. Теплоотдача при свободном движении жидкости.
- •4.1 Свободный теплообмен в неограниченном пространстве около верикальной плиты или трубы.
- •4.2 Теплоотдача при свободном движении около горизонтальной трубы.
- •4.3 Движение жидкости около нагретых горизонтальных плоских стенок.
- •4.4 Теплоотдача при свободном движении жидкости в ограниченном пространстве.
- •2)Если ширина щели мала, внутри щели возникают циркуляционные контуры.
- •5.Теплообмен при кипении жидкости
- •5.1.Основные представления о процессе кипения
- •Режимы кипения
- •Минимальный радиус пузырька
- •Отрывной диаметр пузырька
- •Кривая кипения
- •Влияние некоторых факторов на интенсивность теплоотдачи при кипении
- •5.2Кризисы кипения
- •Первый кризис кипения
- •Второй кризис кипения
- •5.3.Пузырьковое кипение
- •5.3.1.Пузырьковое кипение жидкости в неограниченном объеме
- •5.3.2.Расчет теплоотдачи при пузырьковом кипении жидкости в неограниченном объеме
- •5.3.3Пузырьковое кипение в условиях вынужденного движения в трубах.
- •Структура двухфазного потока
- •Вертикальные трубы
- •Горизонтальные и наклонные трубы
- •Структура потока при кипении жидкости внутри горизонтальной трубы.
- •Изменение избыточной температуры стенки по периметру при кипении жидкости внутри горизонтальной трубы.
- •5.3.4.Зависимость теплоотдачи от параметра х. Кризис кипения второго рода
- •5.3.5.Расчет теплоотдачи при кипении в трубах
- •5.4. Пленочное кипение жидкости
- •5.4.1. Теплоотдача при ламинарном движении паровой пленки
- •5.4.2.Теплоотдача при турбулентном движении паровой пленки
- •6. Излучение.
- •6.1. Основные законы теплового излучения
- •6.1.1. Виды лучистых потоков
- •6.1.2. Законы теплового излучения твердого тела. Закон Планка
- •Закон смещения Вина
- •Закон Стефана – Больцмана
- •Закон Кирхгофа
- •Закон Ламберта
- •6.2 Теплообмен излучением в системе произвольно расположенных тел
- •Частные случаи
- •6.2.1.Теплообмен излучением при наличии экранов
- •6.3 Излучение газов
- •Отличие излучения газа от излучения твердых тел
- •6.3.1 Теплообмен в поглощающих и излучающих средах
- •Оптическая толщина среды и режимы излучения
- •6.3.2 Излучение паров и газов
- •Основные полосы спектров поглощения и.
- •7. Тепловой расчет теплообменных аппаратов
- •7.1 Основные положения и уравнения теплового расчета
- •Уравнение теплового баланса
- •Уравнение теплопередачи
- •7.2 Вычисление средней разности температур
Закон Ламберта
Законом Стефана - Больцмана определяется количество энергии, которое излучается телом по всем направлениям. Изменение излучения по отдельным направлениям определяется законом Ламберта.
Каждое
направление определяется углом
![]() который оно образует с нормалью к
поверхности.
который оно образует с нормалью к
поверхности.
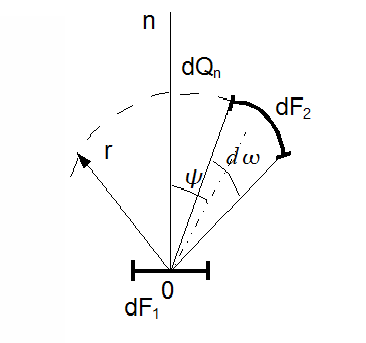
Согласно
закону Ламберта количество энергии,
излучаемое элементом поверхности dF1
в
направление элемента dF2
, пропорционально
количеству энергии излучаемой по
нормали dQn
, умноженному на величину пространственного
угла![]() и
и![]() то есть
то есть
![]() или
или
![]()
где
![]() -
энергия излучения в направлении нормали.
-
энергия излучения в направлении нормали.
Следовательно,
наибольшее количество энергии
поверхностью излучается в направлении
нормали при
![]() С увеличением
С увеличением![]() количество излучаемой энергии уменьшается
и при
количество излучаемой энергии уменьшается
и при![]() оно
становится равным 0.
оно
становится равным 0.
В
этом уравнении неизвестно![]() Для его определения уравнение необходимо
проинтегрировать по поверхности
полусферы, лежащей над плоскостью
Для его определения уравнение необходимо
проинтегрировать по поверхности
полусферы, лежащей над плоскостью![]()
Плоский
угол
![]() в
абсолютных единицах измеряется
отношением
в
абсолютных единицах измеряется
отношением![]() гдеr
— радиус круга, S
— дуга, на которую опирается этот угол.
Бесконечно малый плоский угол измеряется
отношением
гдеr
— радиус круга, S
— дуга, на которую опирается этот угол.
Бесконечно малый плоский угол измеряется
отношением
![]()
Аналогично измеряется и пространственный (телесный) угол:
![]() или
или
![]()
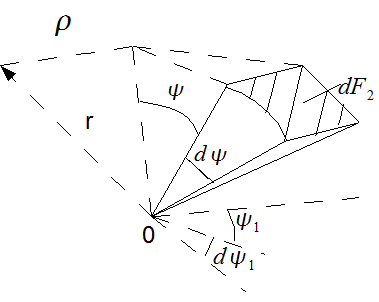
Если
в сферических координатах
![]() обозначает
долготу, а
обозначает
долготу, а![]() -
полярное расстояние (широту), то
направление
-
полярное расстояние (широту), то
направление![]()
![]() и
и![]()
![]() определяют бесконечно малый угол
определяют бесконечно малый угол![]() который на сфере радиусаr
вырезает сферический четырехугольник
который на сфере радиусаr
вырезает сферический четырехугольник
![]() стороны
которого равны:
стороны
которого равны:![]() и
и![]()
Следовательно, телесный угол равен
![]()
![]()
Подставляя полученное выражение в уравнение для Q, получим:
![]()
Проинтегрируем
это выражение по всей поверхности
полусферы, то есть в пределах изменения
угла
![]() от
0 до
от
0 до![]() и
угла
и
угла![]() от 0 до
от 0 до![]() и получим:
и получим:
 или
или
![]() но
но
![]()
Так
как левые части уравнений равны, то,
приравнивая их правые части, определяем
неизвестную
![]()
![]()
Из
этого уравнения следует, что энергия
излученная в направлении нормали в![]() раз
меньше ( полного ) интегрального
полусферического излучения тела,
определяемого по закону Стефана —
Больцмана. После подстановкизакон
Ламберта
принимает вид
раз
меньше ( полного ) интегрального
полусферического излучения тела,
определяемого по закону Стефана —
Больцмана. После подстановкизакон
Ламберта
принимает вид
![]()
Это уравнение служит основой для расчета лучистого теплообмена между поверхностями конечных размеров.
Закон
Ламберта строго справедлив для абсолютно
черного или серого тела. Для тел,
обладающих диффузным излучением, только
в пределах![]()
Для полированных поверхностей закон Ламберта неприменим.
6.2 Теплообмен излучением в системе произвольно расположенных тел
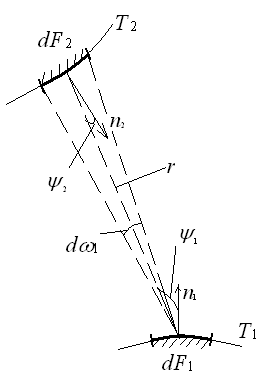
Рассмотрим
два черных тела с изотермическими
поверхностями с температурами Т1
и Т2.
Самооблучение отсутствует, т.е.
![]() .
Необходимо найти поток результирующего
излучения.
.
Необходимо найти поток результирующего
излучения.
Выделим
элементарные площадки
![]() и
и![]() ,
бесконечно малые по сравнению с
расстояниемr
между их центрами.
,
бесконечно малые по сравнению с
расстояниемr
между их центрами.
Лучистый
поток, падающий с элементарной площадки
![]() на площадку
на площадку![]() ,
составит:
,
составит:
![]() .
.
Тепловой
поток, падающий с
![]() на
на![]() ,
равен:
,
равен:
![]() .
.
Элементарные телесные углы можно представить соотношениями:
![]() ;
;
![]() .
.
Яркость излучения каждой из площадок можно выразить через плотность полусферического излучения. Тогда зависимости примут вид:
![]() ;
;
![]() .
.
Введем обозначения:
![]() ;
;
![]() ,
,
где
![]() ,
,![]() -
элементарные угловые коэффициенты
излучения, тогда:
-
элементарные угловые коэффициенты
излучения, тогда:
![]() ;
;
![]() .
.
Здесь
![]() и
и![]() -
полные элементарные потоки собственного
излучения, испускаемые площадками
-
полные элементарные потоки собственного
излучения, испускаемые площадками![]() и
и![]() во всех направлениях.
во всех направлениях.
Из последних зависимостей:
![]() ;
;
![]() .
.
Элементарный угловой коэффициент излучения характеризует долю энергии излучения, которая попадает с элементарной площадки одного тела на элементарную площадку другого тела по отношению к полному лучистому потоку, испускаемому элементарной площадкой первого тела.
Произведение элементарного углового коэффициента излучения на величину соответствующей элементарной площадки называется элементарной взаимной поверхностью излучения.
![]() ;
;
![]() ,
,
тогда:
![]() ;
;
![]() .
.
Введем местные (локальные) значения угловых коэффициентов излучения или местные коэффициенты облученности:
![]() ;
;
![]() .
.
Местные
значения потоков излучения элементарных
площадок
![]() и
и![]() на конечные поверхности
на конечные поверхности![]() и
и![]() :
:
![]() ;
;
![]() .
.
Из этих зависимостей следует:
![]() ;
;
![]() .
.
![]() и
и
![]() носят название местных угловых
коэффициентов излучения. Они характеризуют
долю энергии, испускаемой элементарной
площадкой одного тела на конечную
поверхность другого тела.
носят название местных угловых
коэффициентов излучения. Они характеризуют
долю энергии, испускаемой элементарной
площадкой одного тела на конечную
поверхность другого тела.
Взаимная поверхность излучения:
![]() ;
;
![]() ,
,
при
этом
![]() =
=![]() .
.
Найдем результирующий поток излучения:
![]() .
.
Для
получения
![]() ,
Вт, необходимо это уравнение
проинтегрировать.
,
Вт, необходимо это уравнение
проинтегрировать.
Предварительно введем понятия средних угловых коэффициентов излучения:
![]() ;
;
![]() .
.
Средние угловые коэффициенты позволяют найти:
![]() ;
;
![]() .
.
Результирующий поток излучения определяется разностью:
![]() .
.
Средние угловые коэффициенты излучения через соответствующие лучистые потоки равны:
![]() ;
;
![]() .
.
Средний
угловой коэффициент излучения
характеризует долю энергии, которая
падает с тела, имеющего конечную площадь
поверхности
![]() ,
на другое тело с площадью поверхности
,
на другое тело с площадью поверхности![]() по отношению к полному потоку собственного
излучения первого тела.
по отношению к полному потоку собственного
излучения первого тела.
Средние взаимные поверхности излучения:
![]() ;
;
![]() ,
,
тогда
результирующий поток
![]() определится как:
определится как:
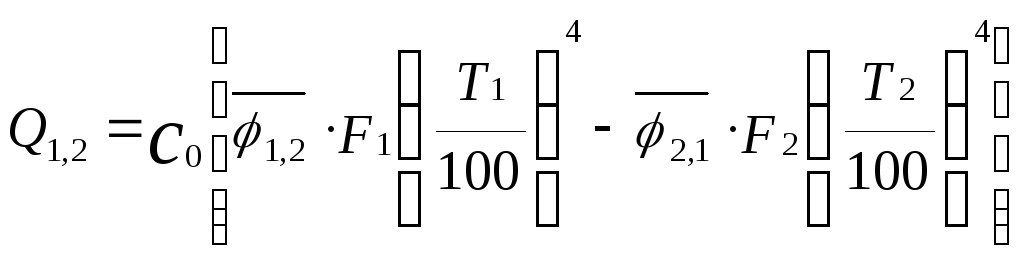 .
.
С
учетом того, что
![]() ,
получим:
,
получим:
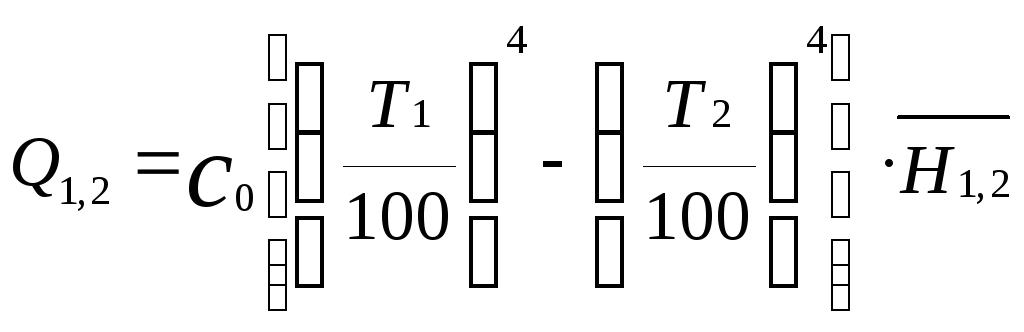 .
.
Если рассматривать излучение серых тел, то для расчета результирующего потока излучения необходимо использовать вместо собственного потока E поток эффективного излучения:
![]() .
.
Используя
свойство взаимности и учитывая, что
результирующий поток можно определить,
как
![]() ,
получим следующую формулу для серых
тел:
,
получим следующую формулу для серых
тел:
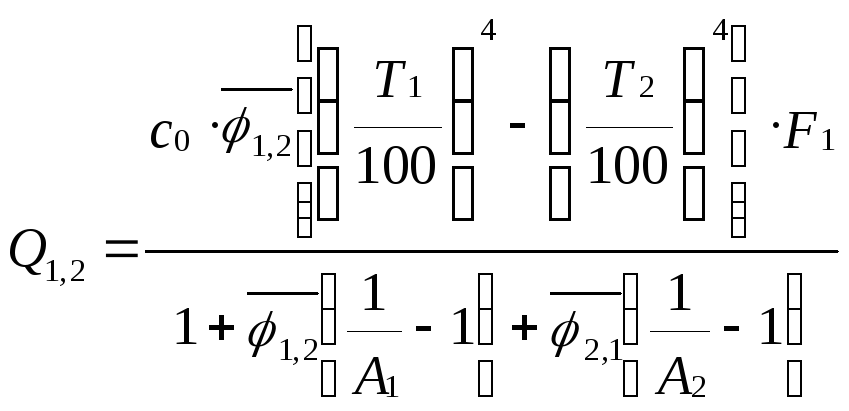 .
.
Угловые коэффициенты являются геометрическими характеристиками и зависят от размеров, формы обоих излучающих тел и их взаимного расположения. Вычисление углового коэффициента представляет большие математические трудности даже для простейших случаев, и поэтому его определяют графическим путем. При решении технических задач значения угловых коэффициентов берутся из таблиц.
