3.5.1. Теплоотдача при ламинарном режиме движения жидкости.

При стабилизированном движении жидкости в трубе теплоотдача является величиной постоянной =const, т.е.

При ;

при ,

где d – определяющий размер,

- температура стенки,

- тепловой поток на стенке.

Вязкостный режим

Течение и теплообмен жидкости у входа в трубу близки к таким же процессам у продольно омываемой пластины, т.к. в начале трубы толщины пограничных слоев малы по сравнению с поперечными размерами канала.

Поэтому теплоотдачу на начальном участке трубы можно описать уравнениями для продольно – обтекаемой пластины.

При для расчета местныхпри вязкостном режиме предложена формула:

,

- поправка, которая учитывает влияние кривизны канала и стеснение потока стенками.

Определяющий размер – x - расстояние от начала трубы.

Определяющая температура – средняя в данном сечении температура жидкости.

Формула применима при .

Среднее значение для начального участка:

Если длина трубы значительно больше длины начального теплового участка, то среднее значение можно определить:

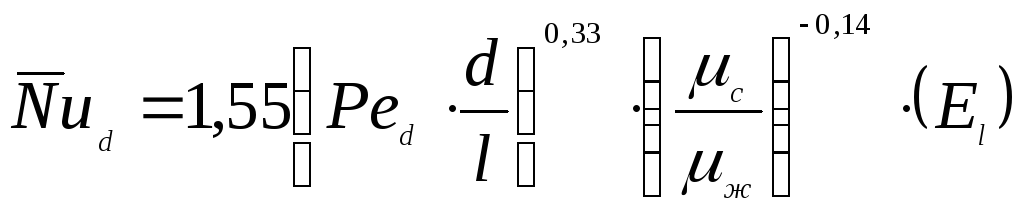, (при );

где - коэффициент динамической вязкости при температуре стенки;

- коэффициент динамической вязкости в ядре потока при температуре жидкости;

- поправка на участок гидродинамической стабилизации (по графику).

Определяющий размер - внутренний диаметр трубы. Свойства жидкости выбираются по температуре ;

- среднелогарифмический температурный напор.

Поправка на вязкость учитывается только для капельных жидкостей.

Вязкостно-гравитационный режим имеет место при .

Число Грасгофа .

Коэффициенты теплоотдачи выше, чем при вязкостном режиме, т.к. влияет естественная конвекция.

Средний коэффициент теплоотдачи определяется:

,

где - поправка на изменение вязкости для капельных жидкостей;

Определяющая температура – средняя температура жидкости в трубе.

Определяющий размер – внутренний диаметр трубы.

- коэффициент, учитывающий изменение по длине трубы.

Если тоE=1,

если тоEпринимают по таблице.

3.5.2. Теплоотдача при турбулентном режиме движения жидкости в трубах.

При >10наступает турбулентный режим течения.

Для расчета среднего коэффициента теплоотдачи Михеевым предложена формула:

.

Если тоE=1, если тоE= .

На газы поправка не распространяется, и для теплоотдачи газов:

3.5.3. Теплоотдача при переходном режиме

2<<10⁴

Течение носит неустойчивый и сложный характер, что затрудняет количественное описание процесса теплообмена. Обобщенные методики расчета теплообмена в переходной области отсутствует. Для оценки теплообмена используют формулы либо турбулентного, либо ламинарного режимов (наибольшее и наименьшее ).

3.5.4. Теплоотдача в трубах некруглого поперечного сечения.

Расчет теплоотдачи производят по тем же формулам, заменяя некруглое сечение некоторой эквивалентной трубой круглого поперечного сечения с диаметром:

,

где - поперечное сечение трубы,

P – смоченный периметр поперечного сечения.

При турбулентном течении в кольцевом канале коэффициент теплоотдачи определится:

,

где d=d- d.