Лекции № 6 - 7 по теме: «Виды статистических критериев»

В области статистики и биометрии в частности применяют два вида статистических критериев: параметрические, построенные на основании параметров данной совокупности (например, и s²_x) и представляющие функции этих параметров, и непараметрические, представляющие собой функции, зависящие непосредственно от вариант данной совокупности с их частотами. Первые служат для проверки гипотез о параметрах совокупностей, распределяемых по нормальному закону, вторые — для проверки рабочих гипотез независимо от формы распределения совокупностей, из которых взяты сравниваемые выборки. Применение параметрических критериев связано с необходимостью вычисления выборочных характеристик — средней величины и показателей вариации, тогда как при использовании непараметрических критериев такая необходимость отпадает.

При нормальном распределении признака параметрические критерии обладают большей мощностью, чем непараметрические критерии. Они способны более безошибочно отвергать нулевую гипотезу, если она не верна. Поэтому во всех случаях, когда сравниваемые выборки взяты из нормально распределяющихся совокупностей, следует отдавать предпочтение параметрическим критериям.

В случае очень больших отличий распределений признака от нормального вида следует применять непараметрические критерии, которые в этой ситуации оказываются часто более мощными. В ситуациях, когда варьирующие признаки выражаются не числами, а условными знаками, применение непараметрических критериев оказывается единственно возможным.

Из параметрических критериев в статистике и биометрии применяют t-критерий Стьюдента и F-критерий Фишера. Первый используют для сравнительной оценки средних величин, второй — для оценки дисперсий. Ниже рассмотрен отдельно каждый из этих критериев.

Параметрические критерии

t-критерий Стьюдента (t-распределение). Английский математик В. Госсет (печатавшийся под псевдонимом Стьюдент), в 1908 г. нашел закон распределения величины , в которой генеральный параметр σ заменен на его выборочную характеристику s_x, т. е. нашел закон распределения значений

.

Открытый Стьюдентом и теоретически обоснованный Р. Фишером закон t-распределения служит основой так называемой теории малой выборки, которая характеризует распределение выборочных средних в нормально распределяющейся совокупности в зависимости от объема выборки. t-распределение зависит только от числа степеней свободы k = n—1, причем с увеличением объема выборки п t-распределение быстро приближается к нормальному с параметрами μ = 0 и σ = 1 и уже при n>30 не отличается от него. Это видно из табл. 1, в которой приведены табулированные значения t-распределения и нормального распределения для разных значений t.

Таблица 1

Распределение	Нормированное отклонение t
	0,5	1.0	1.5	2,0	2,5	3,0	3,5
Нормальное	0,383	0,683	0,866	0,955	0,988	0,997	0,9995
Стьюдента при n = 3	0,333	0,577	0,728	0,816	0,870	0,905	0,927
n = 20	0,377	0,670	0,850	0,940	0,978	0,993	0,998
n = 30	0,383	0,683	0,866	0,955	0,988	0,997	0,9995

Более наглядное представление о характере t-распределения дает рис.1, на котором на фоне нормальной кривой изображена (более пологая) кривая t-распределения при n=3.

t-распределение симметрично и отражает специфику распределения средней арифметической в случае малой выборки в зависимости от ее объема (n). Для выборок, объем которых превышает 30 единиц, величина t распределяется нормально и не зависит от числа наблюдений. Если же n<30, характер t- распределения находится в зависимости от числа наблюдений n.

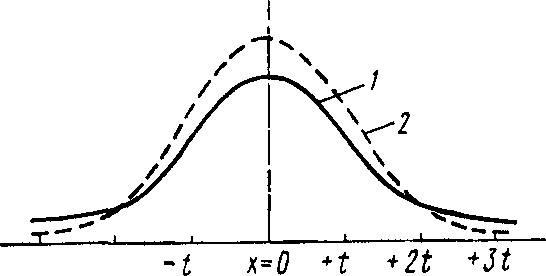
Рис. 1. Кривая t-распределения (1) при n = 3 на фоне нормальной кривой (2)

Для практического использования t-распределения составлена специальная таблица (см. табл. 1 Приложения), в которой содержатся критические точки для разных уровней значимости α и чисел степеней свободы k. Как пользоваться этой таблицей в разных случаях применения t-критерия, мы рассмотрим чуть позднее.

Оценка разности средних. Сравнивая друг с другом две независимые выборки, взятые из нормально распределяющихся совокупностей с параметрами μ₁ и μ₂. Разность μ₁- μ₂ этих параметров обозначим через D, то есть μ₁- μ₂=D, а дисперсию этой разности σ²_D. Значения генеральных параметров неизвестны, однако по выборкам мы можем найти величины выборочных средних и разность между ними , которую обозначимd, то есть

Нулевая гипотеза сводится к предположению, что μ₁=μ₂, то есть D=0. Критерием для проверки H₀-гипотезы служит отношение

где t — переменная величина, следующая t-распределению Стьюдента с числом степеней свободы k = n₁ +n₂ — 2, а s_D - ошибка указанной разности, а n₁ и n₂ - объемы первой и второй выборок соответственно.

Так как, согласно H₀-гипотезе, μ₁=μ₂, то t-критерий выражается в виде отношения разности выборочных средних к своей ошибке, т. е.

.

H₀-гипотезу отвергают, если фактически установленная величина t-критерия (обозначаемая t_ф) превзойдет или окажется равной критическому значению t_kp этой величины для принятого уровня значимости α и числа степеней свободы k = n₁ +n₂ — 2, т. е. при условии t_ф ≥ t_kp.

Ошибку разности средних s_D определяют по формуле:

Пример 1. Изучали влияние кобальта на массу тела кроликов. Опыт проводили на двух группах животных: опытной и контрольной. Были исследованы кролики в возрасте от полутора до двух месяцев, массой тела 500—600 г. Опыт продолжался полтора месяца. Животных обеих групп содержали на одном и том же кормовом рационе. Однако опытные кролики в отличие от контрольных ежедневно получали добавку к рациону в виде водного раствора по 0,06 г хлористого кобальта на 1 кг живой массы тела. За время опыта животные дали следующие прибавки живой массы тела:

Таблица 2.

Привесы, г		Отклонения от средней арифметической		Квадраты отклонений
опыт	контроль	опыт	контроль	опыт	контроль
580	504	58	22	3364	484
692	560	54	34	2916	1 156
700	420	62	106	3844	11236
621	600	17	74	289	5 476
640	580	2	54	4	2916
561	530	77	4	5929	16
680	490	42	36	1764	1 296
630	580	8	54	64	2916
	470		56	ч	3136
Σ = 5104	Σ = 4734	——	——	Σ =18 174	Σ = 28 632
=638	=526	——	——	Σ = 46 806

Средние арифметические привесов:

в опыте = 5104/8= 638 г,

в контроле =4734/9 = 526 г. Разница =d = 112 г. Чтобы установить, достоверна или случайна эта разница, нужно определить ошибку разности средних:

Отсюда t_ф = 112/27,14= 4,1.

По табл.1 Приложений для уровня значимости α = 0,01 и числа степеней свободы k = 9+8—2= 15 находим t_kp = 2,95. Так как t_ф > t_kp, нулевая гипотеза опровергается на высоком уровне значимости (Р<0,01). Разница между средними величинами опыта и контроля оказалась в высшей степени достоверной.

Неопровержение H₀-гипотезы нельзя рассматривать как доказательство равенства между неизвестными параметрами совокупностей, из которых извлечены сравниваемые выборки. В таких случаях вопрос о преимуществе одной статистической совокупности перед другой остается открытым. Ведь не исключено, что при повторных испытаниях H₀-гипотеза может оказаться несостоятельной. Более того, и в тех случаях, когда H₀-гипотеза опровергается, не следует спешить с окончательным выводом.

Следует заметить, что вышеизложенное применение t-критерия предполагает, что дисперсии сравниваемых групп одинаковы. Если это не так, то величину критерия находят по модифицированной формуле:

,

а число степеней свободы — по формуле:

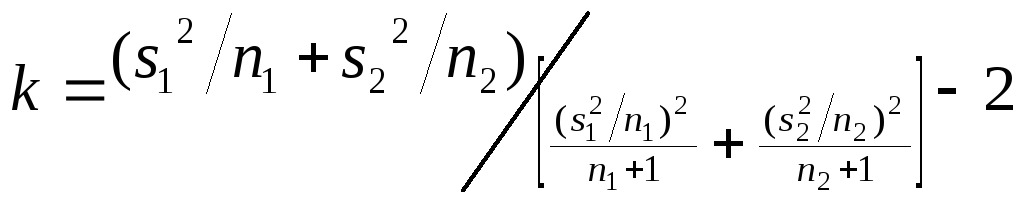
Так, при изучении влияния кобальта на массу тела кроликов дисперсии составляют и (см. табл.2). Видно, что s²₂>s²₁.

Следовательно, величину критерия необходимо определять с учетом неравенства дисперсий.

Предварительно найдем = 2596,3/8=324,54 и s²₂/n₂ = 3579,0/9=397,67.

Величина t-критерия равна

t_ф =

Затем определяем число степеней свободы k. В результате k = 722,2²/27516,6—2 = 17. Для k=17 и α = 0,01 в табл. 1 Приложения находим t_kp = 2,90. Так как t_ф > t_kp, то H₀-гипотеза по-прежнему отвергается.

Правильное применение t-критерия предполагает нормальное распределение совокупностей, из которых извлечены сравниваемые выборки, и равенство генеральных дисперсий. Если эти условия не выполняются, то t-критерий применять не следует. В таких случаях более эффективными будут непараметрические критерии.

t-критерий Стьюдента применяется также и для сравнения некоторых других параметров выборок.

F-критерий Фишера (F-распределение). Для проверки H₀-гипотезы о равенстве генеральных дисперсий (σ²₁ = σ²₂) нормально распределяющихся генеральных совокупностей t-критерий оказывается недостаточно точным, особенно при оценке разности дисперсий малочисленных выборок. В поисках лучшего критерия Р. Фишер нашел, что вместо выборочной разности s₁—s₂ удобнее использовать разность между натуральными логарифмами этих величин, т. е. ln s₁—ln s₂, где s₁. ≥s₂. Эта разность, обозначенная Фишером буквой z, распределяется нормально при наличии как больших, так и средних по объему статистических совокупностей.

Д. Снедекор предложил вместо логарифма отношений использовать отношения выборочных дисперсий, обозначив этот показатель в честь Фишера буквой F, т. е.

.

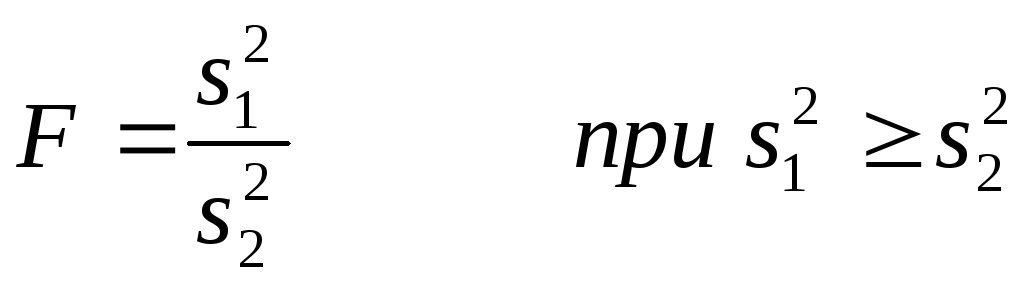Так как принято брать отношение большей дисперсии к меньшей, то критерий F ≥ 1. Чем значительнее неравенство между выборочными дисперсиями, тем больше будет и величина F, и, наоборот, чем меньше окажется разница между дисперсиями, тем меньше будет величина F.

Величина F имеет непрерывную функцию распределения и зависит только от чисел степеней свободы k₁ = n₁—1 и k₂ = n₂—1.

F полностью определяется выборочными дисперсиями и не зависит от генеральных параметров, так как предполагают, что сравниваемые выборки из генеральных совокупностей с равными дисперсиями σ²₁ = σ²₂ или из одной и той же генеральной совокупности. Функция распределения возможных значений величины F при небольшом п имеет форму асимметричной кривой, которая по мере увеличения числа испытаний приближается к кривой нормального распределения (рис. 2).

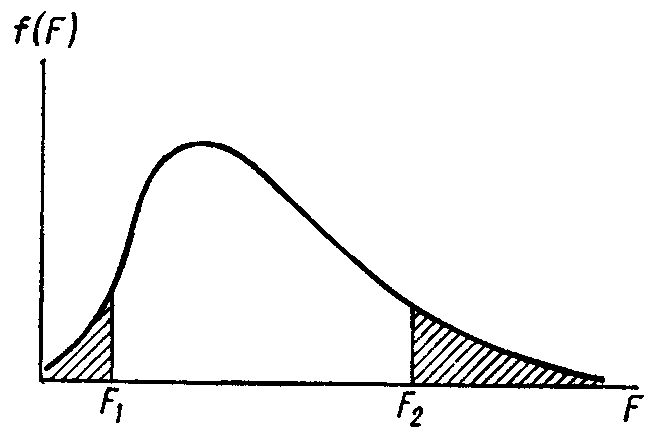
Рис. 2. График плотности вероятности F-распределения.

Функция F-распределения табулирована для 5%-ного (Р = 0,05) и 1%-ного (Р = 0,01) уровней значимости и чисел степеней свободы k₁ для большей дисперсии и k₂ для меньшей. Критические точки для F-критерия содержатся в табл. 2 Приложения. В этой таблице степени свободы для большей дисперсии расположены в верхней строке (по горизонтали), а степени свободы для меньшей дисперсии — в первой графе (по вертикали).

Если сравниваемые выборки извлечены из одной и той же генеральной совокупности или из разных совокупностей с равными друг другу дисперсиями σ²₁ = σ²₂, то величина F-критерия не превысит критические точки (F_kp), указанные в табл. 2 Приложения. Если же выборки взяты из разных совокупностей с их параметрами σ²₁ и σ²₂, не равными друг другу, то F_ф ≥ F_kp и нулевая гипотеза должна быть отвергнута.

Пример 2. В табл. 2 содержатся данные о влиянии кобальта на массу тела кроликов. Рассчитанные для этих данных дисперсии таковы: в опытной группе s²₁ = 2596,3, в контроле s²₂ = 3579,0. Дисперсионное отношение F=3579,0/2596,3 = 1,3. В табл. 2 Приложения для 5%-ного уровня значимости (Р=0,05) и чисел степеней свободы k₁ = 9—1=8 (см. верхнюю строку таблицы) и k₂ = 8—1 =7 (см. первую графу той же таблицы) находим F_kp =3,5. Так как F_ф < F_kp, нулевая гипотеза остается в силе (P>0,05). Это означает, что генеральные параметры сравниваемых групп σ²₁ = σ²₂ и что применение t-критерия для проверки H₀-гипотезы в отношении оценки разности между выборочными средними и имеет достаточные основания.

F-критерий можно применить и для оценки разности между долями из неравновеликих выборок, и при оценке разности между коэффициентами вариации.