Лекция № 10 по теме: «Элементы линейного регрессионного и корреляционного анализа»

Элементы корреляционной зависимости. Коэффициент корреляции

Зависимость между значениями одной случайной величины и условным математическим ожиданием другой случайной величины носит название статистической.

Чтобы изучить статистическую зависимость, нужно знать условное математическое ожидание случайной величины. Для его оценки необходимо знать аналитический вид двумерного распределения (X,Y). Однако, суждение об аналитическом виде двумерного распределения, сделанного по отдельной ограниченной по объёму выборке, может привести к серьёзным ошибкам. Поэтому идут на упрощение и переходят от условного математического ожидания случайной величины к условному среднему значению, т.е. принимают, что

Зависимость между значениями одной случайной величины и условным средним значением другой случайной величины носит название корреляционной (от англ. correlation - согласование, связь, взаимосвязь, соотношение, взаимозависимость); термин впервые введен Гальтоном в 1888г.

Парный коэффициент корреляции Пирсона (1896 г.) изменяется в пределах от -1 до +1. Значение 0,00 интерпретируется как отсутствие корреляции. Корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу.

Корреляционные зависимости наблюдаются между очень многими признаками организмов – морфологическими, физиологическими, а также между различными биологическими процессами. Различают положительную и отрицательную корреляции. При положительной корреляции с увеличением одного признака увеличивается и другой. Например, с увеличением живой массы коров первотёлок возрастает и удой; чем выше процент жира в молоке, тем выше и процент белка в нём. При отрицательной корреляции с увеличением удоя у коров снижается жирность молока; куры с высокой яйценоскостью имеют более мелкие яйца.

В зоотехнической и ветеринарной практике изучение корреляционной зависимости имеет большое значение. Так, например, для животновода очень важно знать, какова связь между средним удоем за лактацию и процентом жира в молоке, иначе говоря, дают ли более высокоудойные коровы молоко с повышенным содержанием жира или, наоборот, с пониженным и насколько часто встречаются исключения из той или другой зависимости. Или другой пример: из-за отрицательной корреляционной зависимости между высокой молочностью и способностью к откорму невозможно выведение породы, сочетающую высокую молочную продуктивность и высокие мясные качества; между устойчивостью к эймериозу у кур и массой тела существует положительная корреляция, поэтому, чем более упитанные куры, тем менее они предрасположены к заболеванию.

Определяют две черты зависимости между переменными: величину зависимости и надежность зависимости.

Надежность зависимости – менее наглядные понятия, чем величина зависимости, однако чрезвычайно важна. Оно непосредственно связано с репрезентативностью той определенной выборки, на основе которой строятся выводы. Другими словами надежность говорит, насколько вероятно, что зависимость подобная найденной, будет вновь обнаружена (подтвердится) на данных другой выборки, извлеченной из той же самой популяции. Если исследование удовлетворяет некоторым специальным критериям, то надежность найденных зависимостей между переменными выборки можно количественно оценить и представить с помощью стандартной статистической меры (называемой р-уровень, или статистический уровень значимости).

Статистическая значимость результата представляет собой оцененную меру уверенности в его правильности. Уровень значимости или р-уровень, - это показатель, находящийся в убывающей зависимости от надежности результата. Более высокий р-уровень соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно р-уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию. Чем слабее зависимость между переменными, тем большего объема требуется выборка, чтобы значимо ее обнаружить. Другими словами, если зависимость между переменными почти отсутствует, объем выборки, необходимый для ее значимого обнаружения, почти равен объему всей популяции, которой предполагается бесконечным.

Рабочие формулы коэффициентов корреляции применяют с учетом того, с какой выборкой (большей или малой) мы имеем дело.

Например, для малых выборок удобнее всего пользоваться следующей формулой:

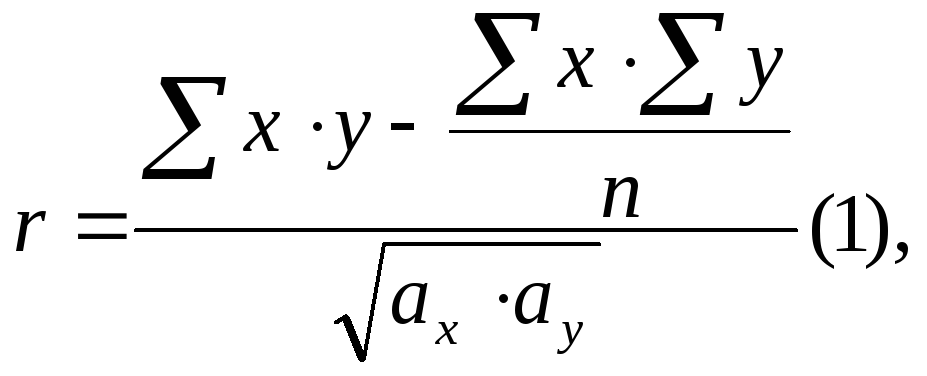, где

и , где х-варианты первого признака;

у-варианты второго признака; n-число наблюдений в выборке.

Вспомогательная таблица для расчетов коэффициента корреляции.

№	X	Y	XY	X2	Y2
1
2
…
=	=	=	=	=	=

Коэффициент корреляции, возведенный в квадрат, называется коэффициентом детерминации r². Он показывает долю изменений, которые вызваны факторным признаком. Коэффициент детерминации r² является прямым способом выражения зависимости одного признака от другого. Если известно, что У находится в причинной связи с Х, то r² – это доля вариации У, обусловленная влиянием Х.

Пример. Определить величину и направление связи между живой массой бройлеров (г) (кросс «Смена – 4», реконструированные птичники) и убойным выходом птицы (%).

Решение. Пусть Х – значения живой массы бройлеров, Y – убойный выход бройлеров, n = 13.

Составим вспомогательную таблицу для расчетов r .

N	X	Y	X2	Y2	XY
1	1940	71,0	3763600	5041,00	137740,0
2	2066	72,1	4268356	5198,41	148958,6
3	1935	71,8	3744225	5155,24	138933,0
4	1946	71,8	3786916	5155,24	139722,8
5	1785	71,4	3186225	5097,96	127449,0
6	1780	72,7	3168400	5285,29	129406,0
7	1898	72,5	3602404	5256,25	137605,0
8	1726	71,6	2979076	5126,56	123581,6
9	1810	70,5	3276100	4970,25	127605,0
10	1808	70,8	3268864	5012,64	128006,4
11	1846	72,0	3407716	5184,00	132912,0
12	1621	70,5	2627641	4970,25	114280,5
13	1889	71,2	3568321	5069,44	134496,8
	24050	929,9	44647844	66522,53	1720697

Подставляем полученные данные в формулу (1).

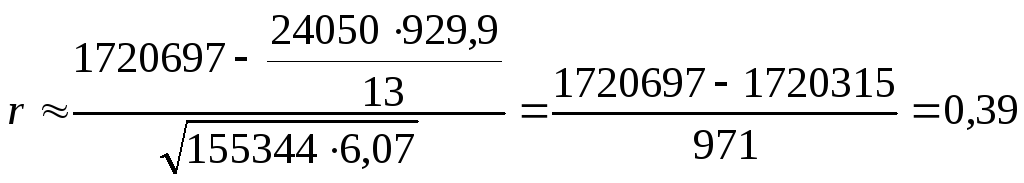
Следовательно, теснота связи между данными признаками средняя, зависимость положительная.

r²=0,15 = 15% - коэффициент детерминации. Он показывает, что 15% вариации убойного выхода птицы данного кросса обусловлено живой массой бройлеров.

Формула для расчета коэффициента корреляции для больших выборок выглядит следующим образом: (2), где и - срединные значения интервалов,

и - средние квадратические отклонения признаков Х и У соответственно.

Для вычисления суммы в формуле (2) составляют корреляционную решетку.

Основу решетки составляют интервалы одного признака, а по вертикали – интервалы другого. На пересечении строк и столбцов находятся частоты n_xy наблюдаемых пар значений признаков и произведения . В строке

n_y записаны суммы частот столбцов. В столбце n_x записаны суммы частот строк. В клетке на пересечении n_x и n_y помещена сумма всех частот. В нижнем правом углу подсчитывается , которая входит в формулу для подсчета выборочного коэффициента корреляции.

Разберем на примере вычисления коэффициента корреляции для большой выборки.

Например, необходимо выявить, существует ли зависимость между высшим суточным удоем и удоем за лактацию у 100 коров. Для этого воспользуемся данными высшими суточными удоями и продуктивности за 300 дней лактации каждой коровы.

Обработка материала начинается с нахождения интервалов по каждому признаку. Рассчитывают средние значения каждого признака , , затем средние квадратические отклонения , .

Затем строим корреляционную решетку на основании найденных интервалов и заполняем ее согласно выше изложенной теории.

Корреляционная решетка высшего суточного удоя (Х) и удоя за лактацию (Y) 100 коров.
Удой за лактацию Высший (Y) суточный удой (X)	1500-1900	1900-2250	2250-2600	2600-2950	2950-3300	3300-3650	3650-4000	4000-4350	4350-4700	4700-5050	nx
10,5-11,7	37740 2	23032,5 1									3	60772,5
11,7-12,9		76567,5 3	59655 2	34132,5 1							6	170355
12,9-14,1		28012,5 1	65475 2	74925 2	42187,5 1						6	210600
14,1-15,3			106942,5 3	163170 4	91875 2	51082,5 1					10	413070
15,3-16,5					49687,5 1	497272,5 9	243270 4	66382,5 1			15	856612,5
16,5-17,7					427500 1	891337,5 15	261630 4	-			27	1580467,5
17,7-18,9					114375 2	445147,5 7	209992,5 3	152805 2			14	922320
18,9-20,1							298350 4	244237,5 3	176475 2		9	719062,5
20,1-21,3							79177,5 1	432112,5 5	93667,5 1		7	604957,5
21,3-22,5									198195 2	106762,5 1	3	304957,5
	2	5	7	7	14	32	16	11	5	1

Полученные данные , , , и найденное число в нижнем правом углу корреляционной решетки подставляем в формулу (2) коэффициента корреляции для большой выборки.

Таким образом, связь между величиной высшего суточного удоя и удоем за лактацию весьма высокая и положительная. .

Это означает, что изменчивость удоя за лактацию на 67% обусловлена высшим суточным удоем.

Линейная регрессия. Коэффициенты регрессии.

Для изучения корреляционных связей большое значение имеет коэффициент регрессии , который показывает, насколько в среднем изменяется признак (Х), если коррелирующий с ним признак (У) изменяется на определенную величину.

Коэффициент регрессии в конкретной выборке имеет два значения, а именно: и , т.е. прямое и обратное влияние признаков друг на друга. Формула для расчета коэффициента имеет вид:

;

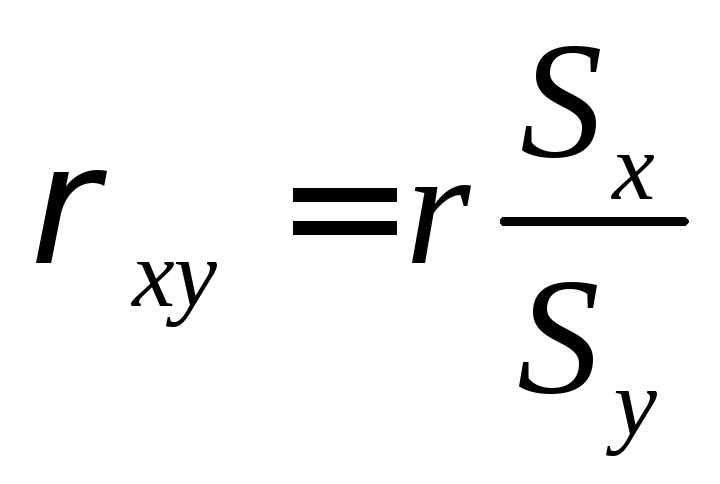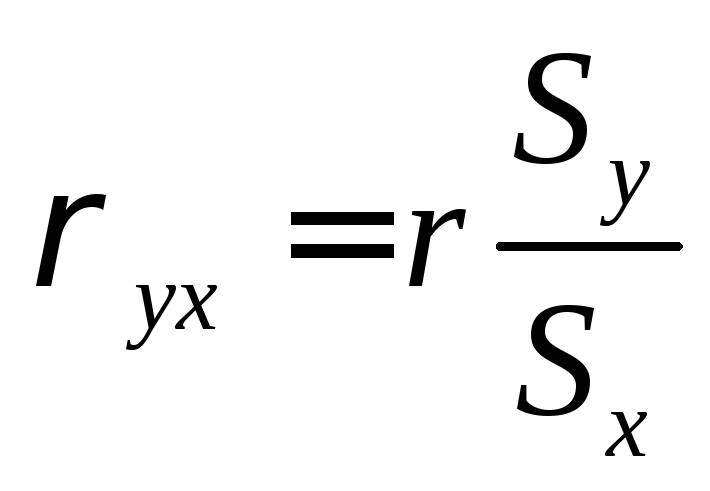
Выше рассматривали пример на вычисление связи между живой массой бройлеров (кросс «Смена-4», реконструированные птичники) и убойным выходом. Связь этих признаков, выраженная через коэффициент корреляции, оказалась средней, r = 0,39, средние квадратические отклонения

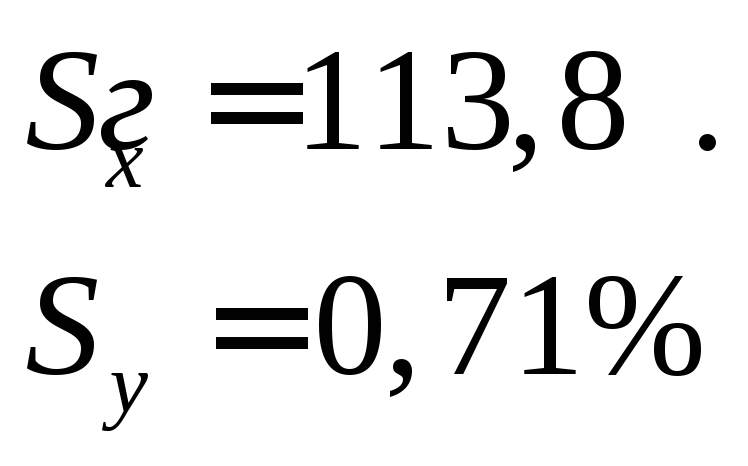
Вычислим коэффициенты регрессии. Подставим полученные данные в формулу коэффициента регрессии.

Регрессия живой массы на убойный выход:

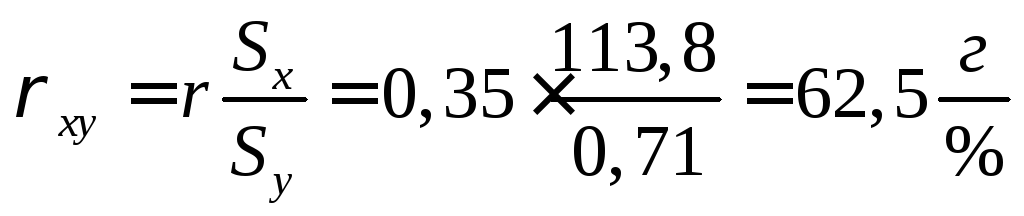, т.е. с увеличением убойного выхода на 1% живая масса бройлеров увеличивается в среднем на 62,5г.

Регрессия убойного выхода на живую массу: , т.е. с увеличением живой массы на

1 г убойный выход увеличивается в среднем на 0,0024%.

Также можно вычислить коэффициент регрессии по формулам:

;

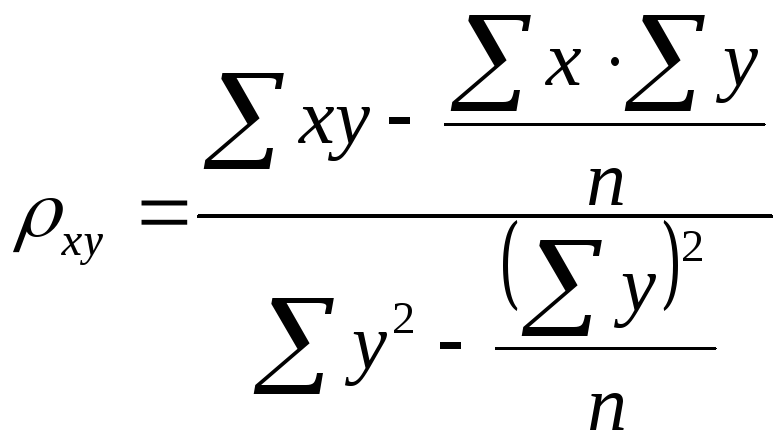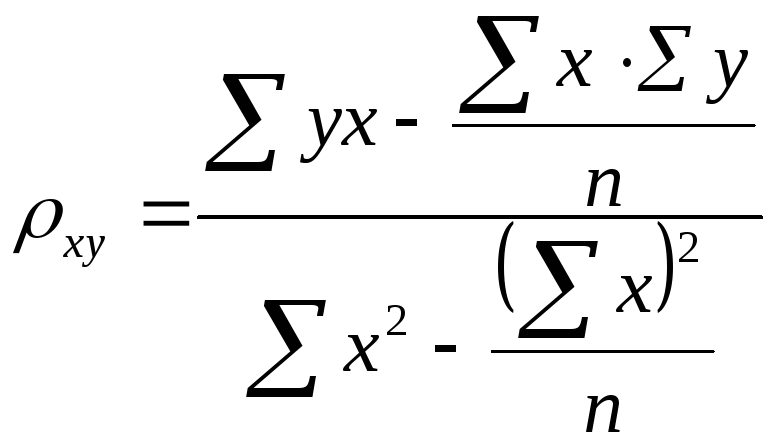
Зная коэффициенты регрессии, можно вычислить коэффициент корреляции:

Уравнение прямой регрессии.

Статистическую зависимость Y от X описывают с помощью уравнения вида

где -условное математическое ожидание величины Y, соответствующее данному значению х; х – отдельные значения величины Х; -некоторая функция. Это уравнение называется уравнением регрессии Y на Х.

Обратную статистическую зависимость можно описать уравнением регрессии X на Y:

где - условное математическое ожидание величины Х, соответствующее данному значению y случайной величины Y; - некоторая функция.

Функции иназывают соответственно регрессиями Y на X и X на Y, а их графики – линиями регрессии Y на Х и X на Y. Уравнения регрессии выражают математическое ожидание случайной величины Y (или X) для случая, когда другая переменная принимает определенное число.

В зависимости от вида уравнений регрессии и формы соответствующих линий регрессии говорят о различной форме статистической зависимости между изучаемыми величинами – линейной, квадратичной, показательной и т.д.

Если функции ,линейные, т.е. уравнения регрессии можно представить в виде:

,

где A,B,C,D – некоторые параметры, то описываемые этими уравнениями зависимости Y от X и X от Y называются линейными; линии регрессии при этом – прямые. Если линия регрессии не является прямой, то такую зависимость называют нелинейной.

Как уже было сказано выше, возможности практического применения статистической зависимости весьма ограниченны. Поэтому для характеристики формы связи между двумя случайными величинами, полученными в результате выборочных наблюдений, используют корреляционную зависимость (или ). Уравнения, описываемые подобной зависимостью, называют выборочными уравнениями регрессии.

Если функции , линейные, то выборочные уравнения линейной регрессии Y на Xи X на Y можно представить в виде:

,

где и - условные средние значения величин Y и X, параметры b и d - оценки B и D, и - выборочные оценки коэффициентов A и C.

Угловые коэффициенты и линий регрессии носят названия выборочных коэффициентов регрессии Y на X и X на Y соответственно. Они определяются как:

; ,

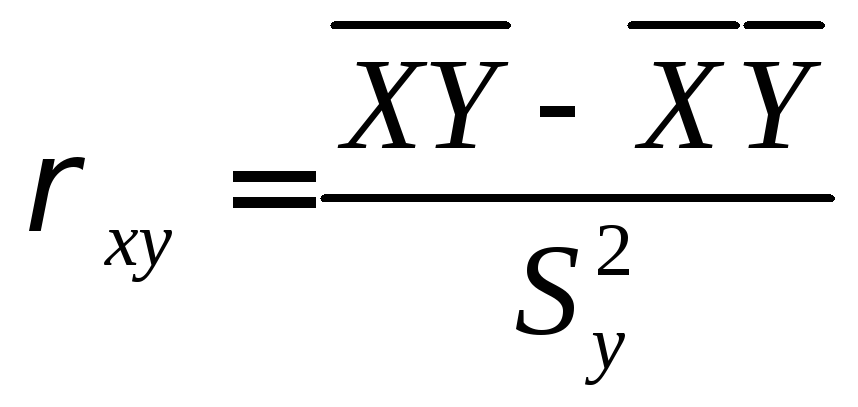где

Из курса аналитической геометрии следует, что коэффициент линейной регрессии (угловой коэффициент линии регрессии) численно равен тангенсу угла наклона линии регрессии к соответствующей оси координат. Следовательно, чем больше, например, коэффициент линейной регрессии Y на X, то есть чем больше угол наклона прямой к оси О_х, тем больше изменяется среднее значение величины Y при изменении значений величины X.

16