Лекция № 3 по теме: «Точность оценки, доверительная вероятность (надёжность). Доверительный интервал»

Как уже было сказано выше, точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, - точечные. При выборке малого объёма точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объёме выборки следует пользоваться интервальными оценками. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надёжность оценок (смысл этих понятий выясняется ниже).

Пусть найденная по данным выборки статистическая характеристика служит оценкой неизвестного параметра. Будем считатьпостоянным числом (может быть и случайной величиной). Ясно, чтотем точнее определяет параметр, чем меньше абсолютная величина разности.Другими словами, еслии, то чем меньше, тем оценка точнее. Таким образом, положительное числохарактеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка удовлетворяет неравенству; можно лишь говорить о вероятности, с которой это неравенство осуществляется.

Надёжностью (доверительной вероятностью) оценки поназывают вероятность, с которой осуществляется неравенство. Обычно надёжность оценки задаётся наперёд, причём в качествеберут число, близкое к единице. Наиболее часто задают надёжность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что , равна:.

Заменив неравенство равносильным ему двойным неравенством

, или , имеем.

Это соотношение следует понимать так: вероятность того, что интервал заключает в себе (покрывает) неизвестный параметр, равна. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Замечание. Интервал имеет случайные концы (их называют доверительными границами). Действительно, в разных выборках получаются различные значения. Следовательно, от выборки к выборке будут изменяться и концы доверительного интервала, т.е. доверительные границы сами являются случайными величинами – функциями от.

Так как случайной величиной является не оцениваемый параметр , а доверительный интервал, то более правильно говорить не о вероятности попаданияв доверительный интервал, а о вероятности того, что доверительный интервал покроет.

Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.

Доверительные интервалы для оценки математического ожидания нормального распределения при известном .

Пусть количественный признак Х генеральной совокупности распределён нормально, причём среднее квадратическое отклонение этого распределения известно. Требуется оценить неизвестное математическое ожидание по выборочной средней. Поставим своей задачей найти доверительные интервалы, покрывающие параметрс надёжностью.

Примем без доказательства, что если случайная величина Х распределена нормально, то выборочная средняя , найденная по независимым наблюдениям, также распределена нормально. Параметры распределениятаковы:

.

Приняв во внимание, что по условию нам задана вероятность , получаем следующую формулу (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через)

.

Смысл полученного соотношения таков: с надёжностью можно утверждать, что доверительный интервалпокрывает неизвестный параметр; точность оценки.

Укажем ещё, что число t определяется из равенства , или; по таблице функции Лапласа находят аргументt, которому соответствует значение функции Лапласа, равное .

Поясним смысл, который имеет заданная надёжность. Надёжность =0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключён; лишь в 5 % случаев он может выйти за границы доверительного интервала.

Доверительным вероятностям, как это видно из таблицы функции Лапласа, соответствуют следующие величины нормированных отклонений:

вероятности ₁=0,95 соответствует t₁₌= 1,96; вероятности ₂= 0,99 соответствует t₂ = 2,58; вероятности ₃= 0,999 соответствует t₃= 3,29.

Выбор того или иного порога доверительной вероятности исследователь осуществляет исходя из практических соображений той ответственности, с какой делаются выводы о генеральных параметрах.

Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном

Пусть количественный признак Х генеральной совокупности распределён нормально, причём среднее квадратическое отклонение неизвестно. Требуется оценить неизвестное математическое ожидание с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором предполагалось известным.

Оказывается, что по данным выборки можно построить случайную величину 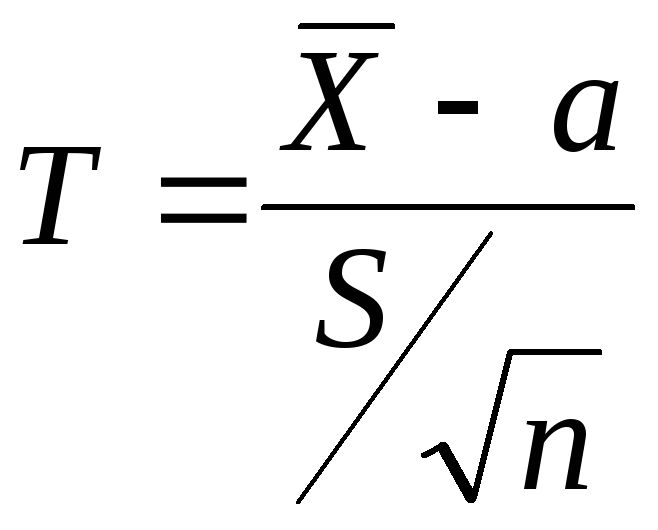, которая имеет распределение Стьюдента сk = n-1 степенями свободы; здесь - выборочная средняя,S – «исправленное» среднее квадратическое отклонение, n – объём выборки.

Пользуясь распределением Стьюдента, находим:

.

Значит, доверительный интервал , покрывает неизвестный параметрc надёжностью . По таблице приложения 1 по заданнымn и можно найти.

Пример 2. Случайная величина Х – вес полугодовалого поросенка в хозяйстве (то есть в генеральной совокупности) - распределена нормально. По выборке объёма n = 16 найдены выборочная средняя =20,2 кг и «исправленное» среднее квадратическое отклонениеs=0,8 кг. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надёжностью 0,95.

Решение. Найдём . Пользуясь таблицей приложения 1, по=0,95 иn = 16 находим =2,13.

Найдём доверительные границы:

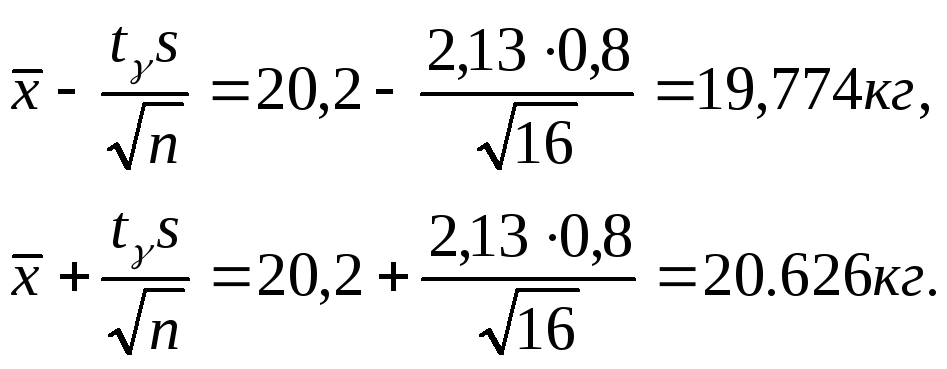
Итак, с надёжностью 0,95 неизвестный параметр заключён в доверительном интервале 19,774<<20,626 (кг).

Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения

Пусть количественный признак Х генеральной совокупности распределён нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение по «исправленному» выборочному среднему квадратическому отклонениюs.

Доверительный интервал, покрывающий параметр с заданной надёжностьюнаходят по следующей формуле:

.

Здесь параметр q определяют, пользуются таблицей приложения 2, а s находят по выборке.

Пример 3. Случайная величина Х – вес полугодовалого поросенка в хозяйстве – (то есть в генеральной совокупности) распределён нормально. По выборке объёма n=25 найдено «исправленное» среднее квадратическое отклонение s=0,8 кг. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надёжностью 0,95.

Решение. По таблице приложения 2 по данным =0,95 иn=25 найдём q=0,32.

Искомый доверительный интервал таков:

0,8 (1 - 0,32)< <0,8 1(1+0,32), или

0,544<<1,056 (кг).

Замечание. Если q>1, то неравенство примет вид

0<<s(1+q).

Пример 4. Количественный признак Х генеральной совокупности распределён нормально. По выборке объёма n=10 найдено «исправленное» среднее квадратическое отклонение s=0,16. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надёжностью 0,999.

Решение. По таблице приложения 2 по данным =0,999 иn=10 найдём q=1,80 (q>1). Искомый доверительный интервал таков:

0<<0,16 (1+1,80), или

0<<0,448.

Приложение 1 (таблица значений )

n				n
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19	2, 78 2, 57 2, 45 2, 37 2, 31 2, 26 2, 23 2, 20 2, 18 2, 16 2, 15 2, 13 2, 12 2, 11 2, 10	4, 60 4, 03 3, 71 3, 50 3, 36 3, 25 3, 17 3, 11 3, 06 3, 01 2, 98 2, 95 2, 92 2, 90 2, 88	8, 61 6, 86 6, 96 5, 41 5, 04 5, 78 4, 59 4, 44 4, 32 4, 22 4, 14 4, 07 4, 02 3,97 3, 92	20 25 30 35 40 45 50 60 70 80 90 100 120	2, 093 2, 064 2, 045 2, 032 2, 023 2, 016 2, 009 2, 001 1, 996 1, 001 1, 987 1, 984 1, 980 1, 960	2, 861 2, 797 2, 756 2, 720 2, 708 2, 692 2, 679 2, 662 2, 649 2, 640 2, 633 2, 627 2, 617 2, 576	3, 883 3, 745 3, 659 3, 600 3, 558 3, 527 3, 502 3, 464 3, 439 3, 418 3, 403 3, 392 3, 374 3, 291

Приложение 2 (таблица для q (γ, n))

n				n
	0,95	0,99	0,999		0,95	0,99	0,999
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19	1,37 1,09 0,92 0,80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39	2,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 o,70 0,66 0,63 0,60	5,64 3,88 2,98 2,42 2,06 1,80 1,60 1,45 1,33 1,23 1,15 1,07 1,01 0,96 0,92	20 25 30 35 40 45 50 60 70 80 90 100 150 200 250	0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 0,143 0,115 0,099 0,089	0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 0,198 0,160 0,136 0,120	0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 0,27 0,211 0,185 0,162