Приложение

Таблица 1. Критические точки t-распределения Стьюдента.

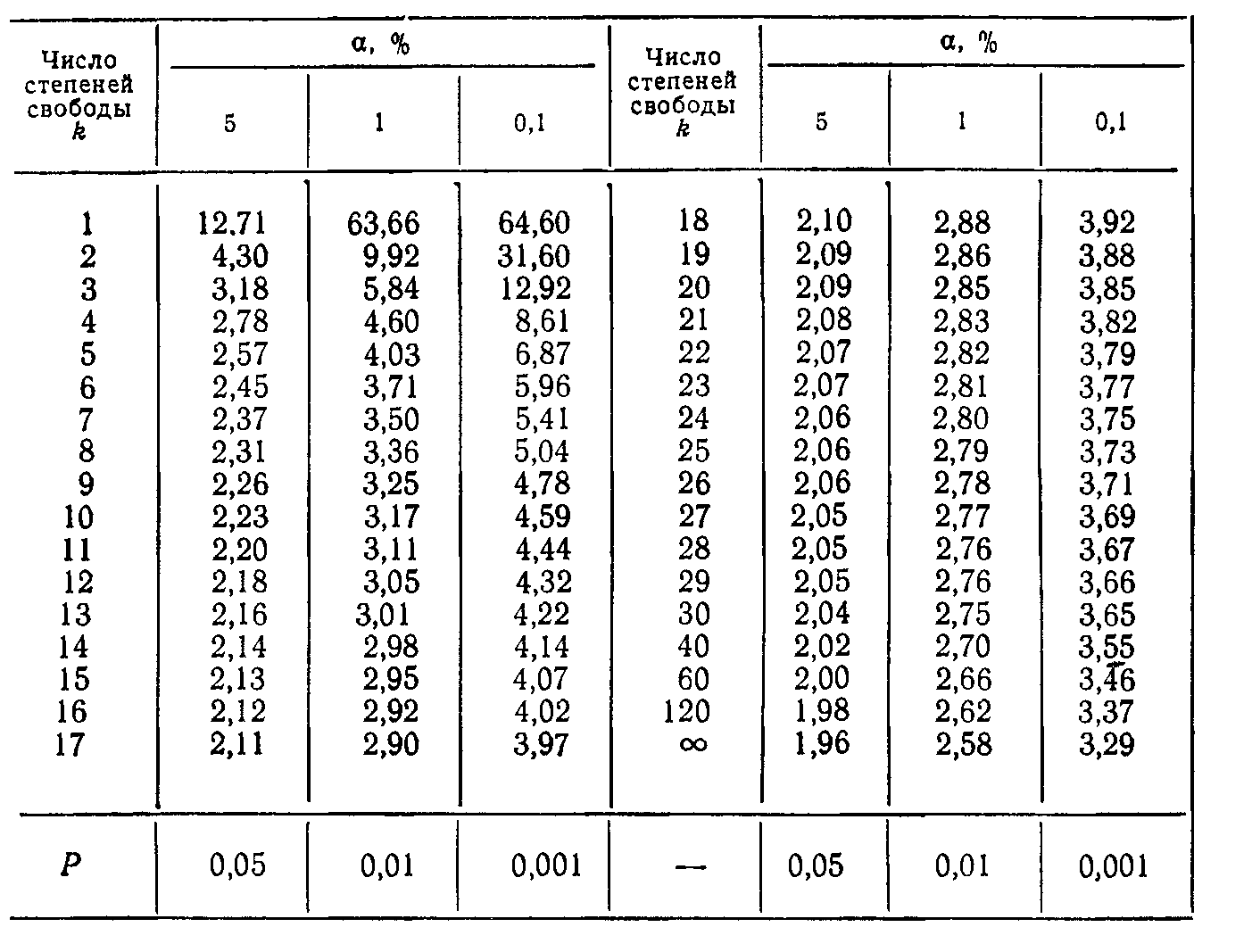
Таблица 2. Значения F-критерия Фишера.

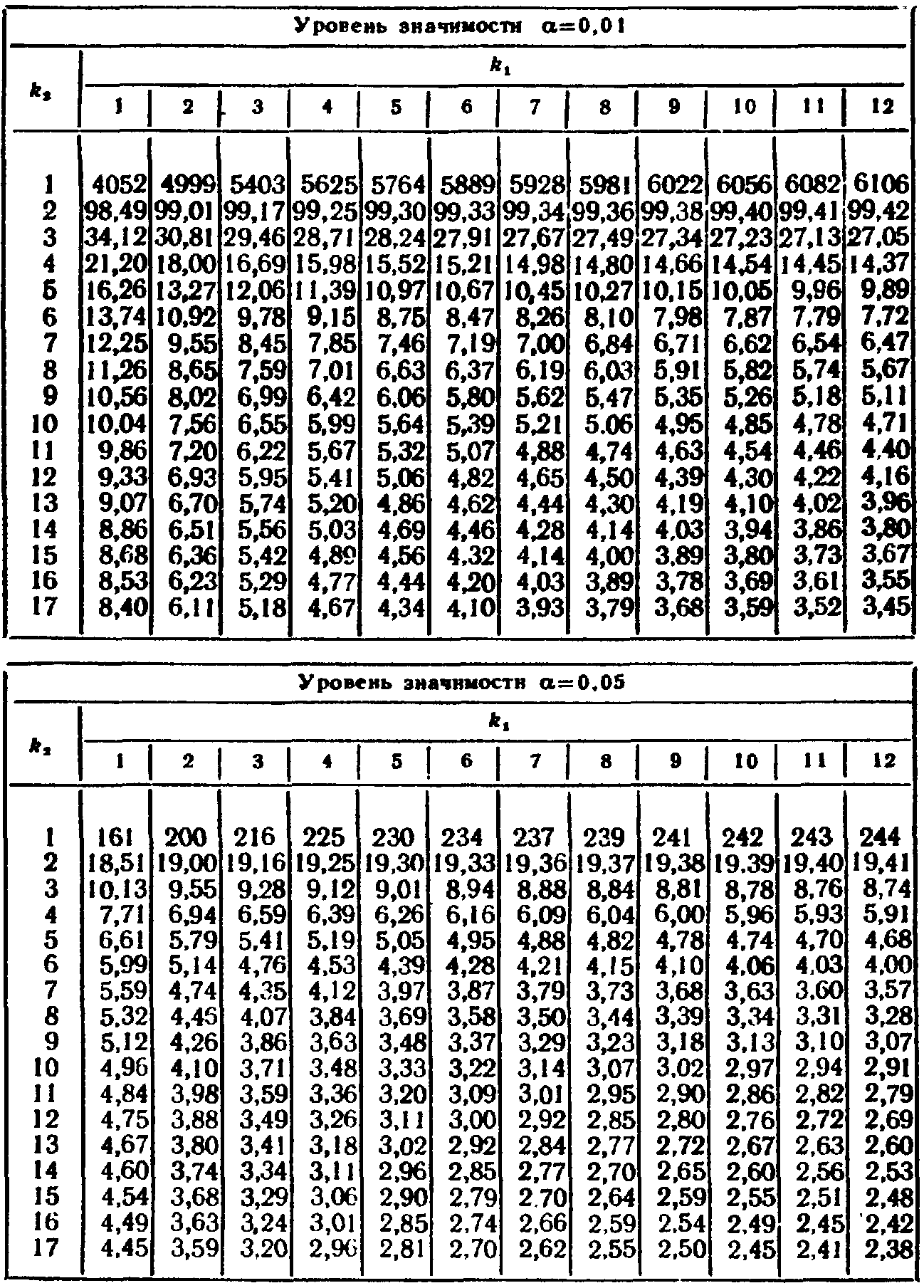
Таблица 3. Критические значения U-критерия (Манна-Уитни) (односторонний критерий, Р = 0,01).

	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
3	0	0	0	0	1	1	1	2	2	2	3	3	4	4	4	5	3
4	0	1	1	2	3	3	4	5	5	6	7	7	8	9	9	10	4
5	I	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	5
6		3	4	6	7	8	9	11	12	14	15	16	18	19	20	22	6
7			6	7	9	11	12	14	16	18	19	21	23	24	26	28	7
8				9	П	13	15	17	20	22	24	26	28	30	32	34	8
9					14	16	19	21	23	26	28	31	33	36	38	40	9
10						19	22	24	27	30	33	36	38	41	44	47	10
11							25	28	31	34	37	41	44	47	50	53	11
12								31	35	38	42	46	49	53	56	60	12
13									39	43	47	51	55	59	63	67	13
14										47	51	56	60	65	69	73	14
15											56	61	66	70	75	80	15
16												66	71	76	82	87	16
17													77	82	88	94	17
18														88	94	100	18
19															101	107	19
20																114	20

Таблица 4. Критические значения z-критерия знаков.

Таблица 5. Критические точки распределения

Число степеней свободы n	Уровень значимости α
	0,01	0,025	0,05	0,95	0,975	0,89
1	6,6	5,0	3,8	0,0039	0,00098	0,00016
2	9,2	7,4	6,0	0,103	0,051	0,020
3	11,3	9,4	7,8	0,352	0,216	0,115
4	13,3	11,1	9,5	0,711	0,484	0,297
5	15,1	12,8	11,1	1,15	0,831	0,554
6	16,8	14,4	12,6	1,64	1,24	0,872
7	18,5	16,0	14,1	2,17	1,69	1,24
8	20,1	17,5	15,5	2,73	2,18	1,65
9	21,7	19,0	16,9	3,33	2,70	2,09
10	23,2	20,5	18,3	3,94	3,25	2,56
11	24,7	21,9	19,7	4,57	3,82	3,05
12	26,2	23,3	21,0	5,23	4,40	3,57
13	27,7	24,7	22,4	5,89	5,01	4,11
14	29,1	26,1	23,7	6,57	5,63	4,66
15	30,6	27,5	25,0	7,26	6,26	5,23
16	32,0	28,8	26,3	7,96	6,91	5,81
17	33,4	30,2	27,6	8,67	7,56	6,41
18	34,8	31,5	28,9	9,39	8,23	7,01
19	36,2	32,9	30,1	10,1	8,91	7,63
20	27,6	34,2	31,4	10,9	9,59	8,26
21	38,9	35,5	32,7	11,6	10,3	8,90
22	40,3	36,8	33,9	12,3	11,0	9,54
23	41,6	38,1	35,2	13,1	11,7	10,2
24	43,0	39,4	36,4	13,8	12,4	10,9
25	44,3	40,6	37,7	14,6	13,1	11,5
26	45,6	41,9	38,9	15,4	13,8	12,2
27	47,0	43,2	40,1	16,2	14,6	12,9
28	48,3	44,5	41,3	16,9	15,3	13,6
29	49,6	45,7	42,6	17,7	16,0	14,3
30	50,9	47,0	43,8	18,5	16,8	15,0

Лекция № 9 по теме: «Элементы дисперсионного анализа»

Дисперсионный анализ – это статистический метод анализа результатов наблюдений, зависящих от различных, одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния. Дисперсионный анализ находит применение в различных областях науки и техники.

Известно, что многие признаки и свойства живых организмов находятся под влиянием различных факторов: наследственности, условий среды, внутренних факторов организма, искусственного отбора. Степень и направленность воздействия различных факторов неодинаковы, поэтому важно определить долю влияния отдельных факторов на изменчивость признака. Для решения подобной задачи используют метод дисперсионного анализа, разработанный Р.Фишером.

Сущность дисперсионного анализа состоит в установлении роли отдельных факторов в изменчивости признака.

В зависимости от количества изучаемых факторов различают однофакторный и многофакторный дисперсионный анализ. Рассмотрим подробнее метод однофакторного дисперсионного анализа.

Однофакторный дисперсионный анализ.

Предположим, что имеется выборок с объемами , , , и наблюдения можно представить в виде , где - номер наблюдения в выборке; - номер выборки; - групповые математические ожидания; - случайные ошибки с =0, о которых предполагается, что они независимы и одинаково расположены.

Подобная ситуация возникает, когда существует некий фактор, принимающий различных значений (называемых уровнями), и каждая группа объектов, чьи признаки мы примеряем, подвергается воздействию определенного уровня этого фактора. Методы математической статистики, изучающие воздействие одного фактора на объекты и их признаки, называют в совокупности однофакторным анализом.

Предполагается, что ошибки нормально распределены: . Тогда можно изучать влияние фактора, вычисляя дисперсии некоторых величин. Совокупность этих методов называют однофакторным дисперсионным анализом.

Основной гипотезой, нуждающейся в проверке, является гипотеза о равенстве групповых средних . Иными словами, проверяют гипотезу о том, что фактор вообще не влияет на наблюдения. В случае нормальных ошибок ее можно проверить, вычислив две разные оценки дисперсии.

Рассмотрим группу экспериментальных животных, подвергнутых ультрафиолетовому облучению. В процессе эксперимента измерялась температура тела животных. Результаты измерений были занесены в таблицу:

№ испытания	Уровень фактора А (мощность ультрафиолетового облучения)
	А1	А2	А3
1 2 3 4	37,4 37,3 37,0 36,9	37,8 37,9 37,5 37,4	38,0 37,9 38,4 38,3
	37,15	37,65	38,15

Физический фактор А (ультрафиолетовое излучение) имеет постоянных уровней (3 различных мощности облучения). На всех уровнях распределения случайной величины Х (температуры тела животного) предполагается нормальным, а дисперсии одинаковыми, хотя и неизвестными.

В данном эксперименте число проведенных наблюдений при действии каждого из уровней фактора одинаково.

Все значения величины Х, наблюдаемые при каждом фиксированном уровне фактора А_j, составляют группу, и в последней строке таблицы представлены соответствующие выборочные групповые средние, вычисленные по формуле

.

Здесь n – число испытаний, – номер столбца, - номер строки, в которой расположено данное значение случайной величины. Общая средняя арифметическая всех наблюдений находится как

.

Введем следующие понятия:

Факторная сумма квадратов отклонений групповых средних от общей средней , которая характеризует рассеивание «между группами» (т.е. рассеивание за счет исследуемого фактора):

,

Остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней , которая характеризует рассеивание «внутри групп» (за счет случайных причин):

.

Общая сумма квадратов отклонений наблюдаемых значений от общей средней :

,

Можно доказать следующее равенство:

.

С помощью , производится оценка общей, факторной и остаточной дисперсий:

,

,

.

В основе однофакторного дисперсионного анализа лежит тесная связь между различием в групповых средних и соотношением между двумя видами дисперсий – факторной, которая характеризует влияние фактора А на величину Х, и остаточной, которая характеризует влияние случайных причин. Сравнивая факторную дисперсию с остаточной по величине их отношения судят, насколько сильно проявляется влияние фактора.

Для сравнения двух дисперсий используют показатель критерия Фишера .

При этом при заданном уровне значимости проверяют нулевую гипотезу о равенстве факторной и остаточной дисперсии (изучаемый фактор не вызывает изменчивости признака) при конкурирующей гипотезе об их неравенстве (изучаемый фактор вызывает изменчивость признака).

По таблице критических значений распределения Фишера – Снедекора (см. приложение 6) при уровне значимости, равном половине заданного уровня , находят критическое значение . Здесь . Если , нулевую гипотезу считают согласующейся с результатами наблюдений. Если , то эту гипотезу отвергают в пользу конкурирующей.

Замечание. Если окажется, что , следует сделать вывод об отсутствии влияния фактора А на Х.

Если проверка покажет значимость различий между и ,следует сделать вывод о существенном влиянии фактора А на Х.

Обычно для упрощенная расчетов фактурную и остаточную дисперсии рассчитывают не по экспериментальным значениям величины Х, а по значениям , где постоянная С представляет собой произвольное число, близкое к среднему значению всех результатов наблюдений.

Вернемся к нашему примеру. Вычтем из всех значений постоянное число С=37,5 близкое к общему среднему =37,51 и составим таблицу:

№ испытания	Уровень фактора А (мощность ультрафиолетового облучения)
	А1	А2	А3
1 2 3 4	-0,1 -0,2 -0,5 -0,6	0,3 0,4 0 -0,1	0,5 0,4 0,9 0,8
	-0,35	0,15	0,65

Общая средняя будет равна

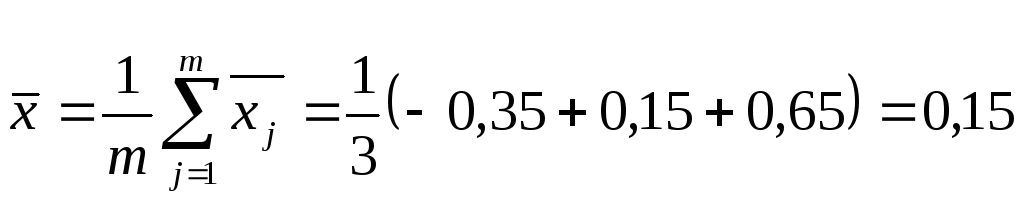
Определим значения _,

Определим значения факторной и остаточной дисперсий:

,

.

Так как , следует проверить значимость их различия. Найдем экспериментальное значение критерия:

.

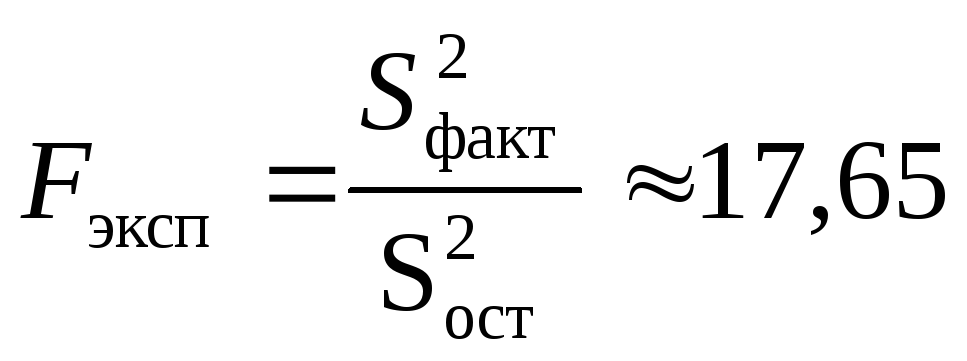Сравним его с критическим значением распределения Фишера – Снедекора для уровня значимости 0,05 (см. приложение 6):

.

Поскольку можно утверждать, что при уровне значимости

=0,05 рассматриваемый физический фактор оказывает влияние на температуру тела животного.

Критерий Фишера указывает на влияние изучаемого фактора (если ) на изменчивость признака. Однако он не указывает на силу влияния этого фактора. В качестве показателя силы влияния фактора на изменчивость признака используют величину:

.

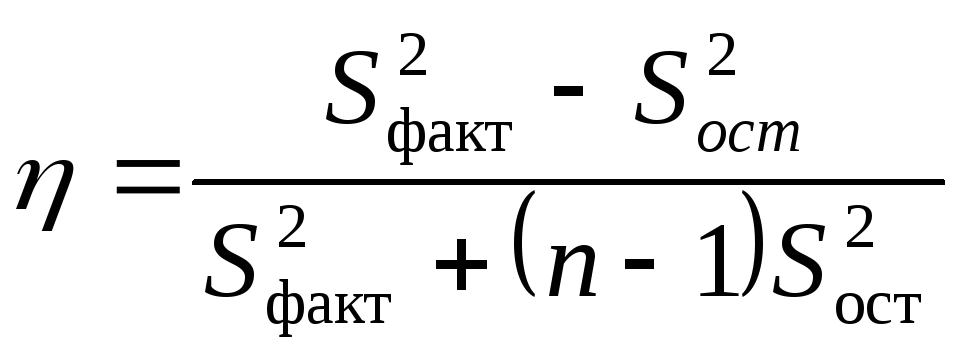Оценим силу влияния ультрафиолетового облучения на повышение температуры тела животных:

или 80,5%

Таким образом, влияние ультрафиолетового облучения на повышение температуры тела животных составляет 80,5%, а 19,5% обусловлены случайными причинами.

Двухфакторный дисперсионный анализ

Двухфакторные комплексы по своей структуре более сложны, чем однофакторные.

Объединение в один статистический комплекс допускается только таких факторов, которые независимы друг от друга (например, тип кормления и доза облучения, возраст и пол и т.д.).

Чтобы построить двухфакторную дисперсионную модель все имеющиеся данные представим в виде табл. 1, в которой по строкам - уровни фактора А, по столбцам - уровни фактора В, а в соответствующих клетках, или ячейках, таблицы находятся значения признака (i=1,2…, m; j=1,2…, l; k=1,2…, n):

Таблица 1.

В А	В1	В2	…	Вj	…	Вl
А1			…		…
А2			…		…
. . .	…	…	…	…	…	…
Аj			…		…
. . .	…	…	…	…	…	…
Аm			…		…

Двухфакторная дисперсионная модель имеет вид:

(1)

где - значение наблюдения в ячейке ij c номером k;

- общая средняя;

- эффект, обусловленный влиянием i-го уровня фактора А;

- эффект, обусловленный влиянием j-го уровня фактора B;

- эффект, обусловленный взаимодействием двух факторов, т.е. отклонение от средней по наблюдениям в ячейке ij от суммы первых трех слагаемых в модели (1);

- возмущение, обусловленное вариацией переменной внутри отдельной ячейки.

Полагаем, что имеет нормальный закон распределения , а все математические ожидания равны нулю.

Групповые средние находятся по формулам:

в ячейке -

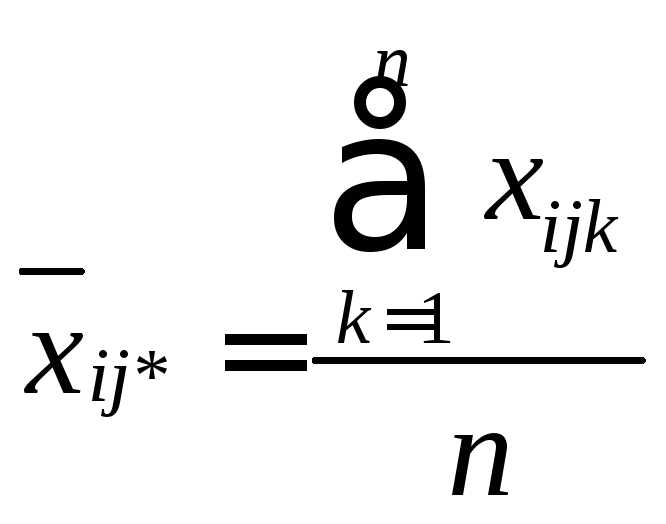(2)

по строке -

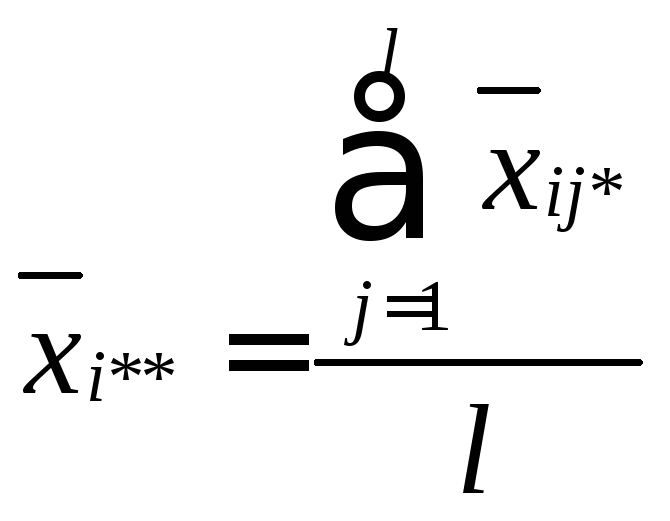, (3)

по столбцу –

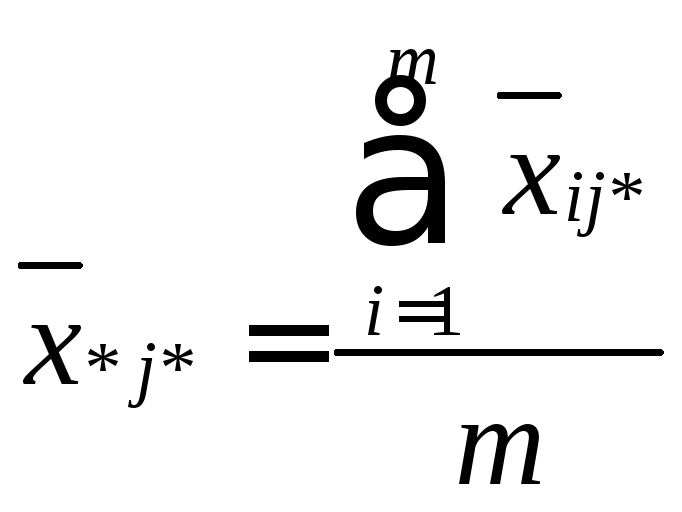(4)

Общая средняя

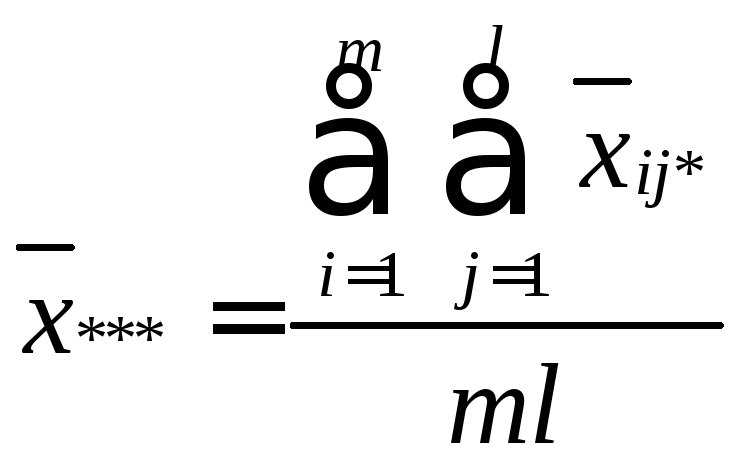(5)

Таблица дисперсионного анализа имеет вид:

Таблица 2

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средние квадраты
Межгрупповая (фактор А)		m-1
Межгрупповая (фактор В)		l-1
Взаимодействие (АВ)		(m-1)(l-1)
Остаточная		mln-ml
Общая		mln-1

Можно показать, что проверка нулевых гипотез об отсутствии влияния на рассматриваемую переменную факторов А, В и их взаимодействия АВ осуществляется сравнением отношений .

Если n=1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены, так как выпадает компонента из общей суммы квадратов отклонений, а с ней и средний квадрат , ибо в этом случае не может быть речи о взаимодействии факторов.

Пример. В табл. 3 приведены суточные привесы (г) отобранных для исследования 18 поросят в зависимости от метода содержания поросят (фактора А) и качества их кормления (фактор В).

Таблица 3.

Количество голов в группе (фактор А)	Содержание протеина в корме, г (фактор В)
	В1=80	В2=100
А1=30	530,540,550	600,620,580
А2=100	490,510,520	550,540,560
А3=300	430,420,450	470,460,430

Необходимо на уровне значимости оценить существенность (достоверность) влияния каждого фактора и их взаимодействия на суточный привес поросят.

Решение. Имеем m=3, l=2, n=3. Определим (в г) средние значения привеса:

в ячейках – по (формуле 2)

и аналогично

;

по строкам – по (3):

и аналогично

по столбцам – (4):

и аналогично

Общий средний привес – по (5):

.

Все средние значения привеса (г) поместим в табл. 3

Таблица 3.

Количество голов в группе (фактор А)	Содержание протеина в корме, г (фактор В)
	В1=80	В2=100
А1=30
А2=100
А3=300

Из табл. 3 следует, что с увеличением количества голов в группе средний суточный привес поросят в среднем уменьшается, а при увеличении содержания протеина в корме - в среднем увеличивается. Но является ли эта тенденция достоверной или объясняется случайными причинами? Для ответа на этот вопрос по формулам табл. 2 вычислим необходимые суммы квадратов отклонений:

;

;

Средние квадраты находим делением полученных сумм на соответствующие им число степеней свободы m-1=2, l-1=1; (m-1)(l-1)=2; mln-ml=18-6=12; mln-1=18-1=17.

Результаты расчета сведем в табл. 4.

Очевидно, данные факторы имеют фиксированные уровни, т.е. мы находимся в рамках модели I. Поэтому для проверки существенности влияния факторов А, В и их взаимодействия АВ необходимо найти отношения:

,

и сравнить их с табличными значениями (см. приложение 6) соответственно Так как и , то влияние метода содержания поросят (фактор А) и качества их кормления (фактор В) является существенным. В силу того что взаимодействие указанных факторов незначимо (на 5%-ном уровне).

Таблица 4.

Компонента дисперсии	Суммы квадратов	Число степеней свободы	Средние квадраты
Межгрупповая (фактор А)		2
Межгрупповая (фактор В)		1
Взаимодействие (АВ)		2
Остаточная		12
Общая		17