Papka_Vz_dlya_bakalavrov_2014g / Папка Вз. Лекции / лекция №13. Вероятностный метод. Основы

Лекция №13

ВЕРОЯТНОСТНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ Р.Ц.

(теоретические основы)

В соответствии с положениями теории вероятностей суммирование случайных величин (размеры деталей, получаемые в процессе обработки (изготовления) этих деталей, рассматриваются как случайные величины) производится квадратически, причём сумме этих величин, в свою очередь, так же случайная величина, изменяющаяся по определённому закону распределения случайных величин.

Закон распределения размеров замыкающего звена тем ближе к закону нормального распределения, чем больше составляющих звеньев имеет размерная цепь. На практике применение вероятностного метода расчёта оправданно, если число составляющих звеньев (А) размерной цепи не менее четырех.

(m-1) ≥ 4.

Поле допуска замыкающего звена А_∆ (рисунок 3.8) определяется по формуле:

,

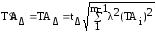(13-01).

где t_Δ – коэффициент риска, выбирается из таблицы 3.2;

λ² – относительное среднее квадратическое отклонение - коэффициент, характеризующий закон рассеяния размеров или их отклонений.

Таблица 13.1.

Риск Р (%)	32,00	10,00	4,50	1,00	0,27	0,10	0,01
Коэф.tΔ (±σ)	1,00	1,65	2,00	2,57	3,00	3,29	3,89

Для закона нормального распределения λ² равно 1/9.

При механической обработке заготовок на настроенных станках распределение полученных размеров подчиняется закону нормального распределения (λ² = 1/9), при сравнительно легком обеспечении размеров, с допусками по (9-10) квалитетам и грубее. При точности обработки по (7-8) квалитетам распределение соответствует закону Симпсона (λ² = 1/6), а при точности по (5-6) квалитетам – закону равной вероятности (λ² = 1/3).

Если принять:

- риск Р = 0,27% (3 детали из 1000 могут иметь размеры, выходящие за пределы их поля допуска);

- коэффициент риска t_Δ = 3;

- число составляющих звеньев (m-1) = 4;

- закон нормального распределения λ² = 1/9,

то формула (13-01) будет иметь вид .

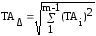(13-02).

Условно приняв TA_i = TA₁ = TA₂ = TA₃ = TA₄ = TA_cp , можно записать

.

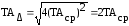(13-03).

Для сравнения, при методе расчётов «max-min»

.

(13-04). Сравнение (13-03) и (13-04) показывает, что допуск составляющего звена при вероятностном методе в два раза (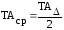) может быть больше, чем при расчётах методом «max-min» ().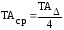

Как следует из теории вероятностей, кривая нормального распределения

,

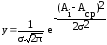(13-05).

Где A_i – конкретный действительный размер;

А_ср – среднее арифметическое размеров деталей данной партии;

σ – среднее квадратическое отклонение.

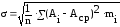, (13-06).

где n – количество деталей в партии (n > 1);

m_i – частота (количество деталей данного интервала размеров).

Кривая нормального распределения имеет вид (рисунок 13.1).

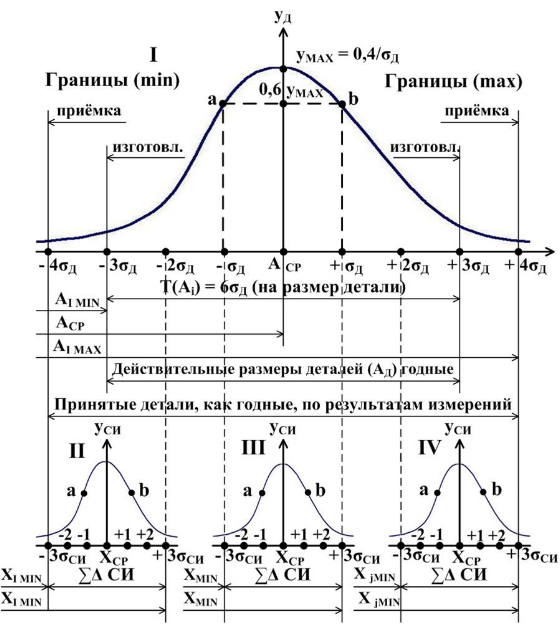
Рисунок 13.1 - Кривая нормального распределения

I – рассеяние размеров деталей в процессе их обработки

(Ai)действит.;

II, III, IV – рассеяние результатов измерений Xi размеров деталей

(Ai)действит. (II - (Ai)д = Aimin; III - (Ai)д = Aiср.; IV - (Ai)д = Ai max);

a, b – точки перегиба кривых распределений

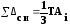
практический ориентир при выборе СИ для конкретных измерений.

На практике поле рассеяния размеров деталей (допуск на размер), принимается равным 6σ, т.е. TA_i = 6σ.

Если суммарная погрешность средства измерения 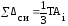, то выход размеров A_i за пределы ±3σ не превышает 0,27%. В пределах ±3σ, годных A_i – 99,73%. Выход размеров деталей (A_i) за границы поля допуска T(A_i) возможен только в случаях II, когда на измерения поступают детали с действительными размерами (A_i)_Д < (A_i)_MIN, либо в случае IV, когда на измерения поступают детали с действительными размерами (A_i)_Д > (A_i)_MAX.

В остальных случаях (например, случай III) суммарная погрешность измерения 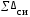обеспечивает измерения X_i размеров детали A_i, невыходящими за пределы поля допуска T(A_i).

Верхнее ES(A_Δ) и нижнее EI(A_Δ) отклонения замыкающего звена при расчётах вероятностным методом определяют по формулам:

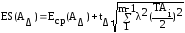, (13-07).

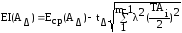. (13-08).

В формулах (13-07) и (13-08) E_ср(A_Δ) – координата середины поля допуска замыкающего звена, которую можно определить по формулам:

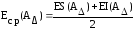. (13-09).

Учитывая, что , можно записать

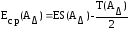или .

(13-10).

Здесь Т(А_Δ) – допуск замыкающего звена, определяемый по формуле (13-01).

6