
- •1. Задачи которые приводят к ду. Понятие ду, его порядок. Решение ду. Общие и частные решения.
- •2. Формы записи дифференциальных уравнений первого порядка. Интегральные кривые. Поле направлений. Метод изоклин.
- •3. Ду с разделяющимися переменными.
- •4. Однородные ду.
- •5. Линейное ду
- •6. Уравнения Бернулли
- •7. Ду в полных дифференциалах.
- •8. Теорема существования и единственности решения ду I-го порядка.
- •9. Ду высших порядков которые интегрируются в квадратурах
- •11. Теорема существования и единственности для системы линейных ду и для линейного ду n-го порядка (без док-ва).
- •12. Линейные уравнения n-го порядка. Линейная зависимость функций. Определитель Вронского. Формула Лиувилля. Фундаментальная система решений.
- •13. Линейное ду второго порядка с переменными коэффициентами. Метод вариации постоянных.
- •14. Однородное линейное ду второго порядка с постоянными коэффициентами.
- •15. Неоднородное линейное ду второго порядка с постоянными коэффициентами и специальной правой частью.
- •16. Приложение линейных ду второго порядка. Свободные вынужденные колебания.
- •17. Линейные ду. Лз функции и вектор-функции. Определитель Вронского. Формула Лиувилля. Фундаментальная система решений.
- •18. Неоднородные линейные дифференциальные системы с переменными коэффициентами.
- •19. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами
- •20. Понятие о системах дифференциальных уравнений. Связь с уравнениями высших порядков.
12. Линейные уравнения n-го порядка. Линейная зависимость функций. Определитель Вронского. Формула Лиувилля. Фундаментальная система решений.
Линейные уравнений n-го порядка имеют вид:

Пусть
даны
 на а<x<b
составим их линейную комбинацию:
на а<x<b
составим их линейную комбинацию:
 Если эта линейная комбинация тождественно
=0 в (а,b)
только при нулевых коэффициентах
Если эта линейная комбинация тождественно
=0 в (а,b)
только при нулевых коэффициентах
 ,
то функции
,
то функции называются линейно не зависимыми в
(а,b)
в противном случае функцию называют
ЛЗ.
называются линейно не зависимыми в
(а,b)
в противном случае функцию называют
ЛЗ.
Две
функции ЛНЗ если их отношения :

Совокупность
решений
 где
где однородного
линейного уравнения
однородного
линейного уравнения ЛНЗ в интервале
ЛНЗ в интервале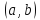 называется фундаментальной системой
решений этого уравнения на
называется фундаментальной системой
решений этого уравнения на
Определитель
составленный из частных решений и их
производных до (n-1)
порядка называется определитель
Вронского:




Свойства
Вронскиана:1) Если W(x)обратим
в ноль в одной точке интервала (a,b)
следовательно он равен нулю на всем
интервале. 2) Если
 хотя бы в одной точке (a,b)
то он отличен от нуля на всех точках
(a,b).
хотя бы в одной точке (a,b)
то он отличен от нуля на всех точках
(a,b).
13. Линейное ду второго порядка с переменными коэффициентами. Метод вариации постоянных.
y’’+
a(x)y’+b(x)y=0
(1) - ОЛДУ второго порядка a(x),b(x)
– непрерывные функции.
 То
То
Пусть

Решая
найдем



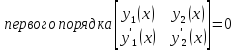

Неоднородные .

Будем использовать решение (4) с помощью метода вариационных произвольных постоянных. (1) – ОДУ, (3) – общее решение.
В
(3) заманим постоянные
 на
на




(3),(5) подставим в (4)

Сгруппируем при с1 и с2. Получим систему .
 (6)
(6)
Решив
(6) способом Крамера:



14. Однородное линейное ду второго порядка с постоянными коэффициентами.
Однородным уравнением с постоянными коэффициентами называется уравнение вида:

Имеет
фундаментальную систему решений
определенных на
 и состоящий из степенных показателей
и тригонометрических функций.
Соответственно и общее решение:
и состоящий из степенных показателей
и тригонометрических функций.
Соответственно и общее решение:
Построим
фундаментальную систему решения
уравнения (1) с помощью метода Эйлера.
Будем искать частное решение вида

 (2)
подставим (1)
(2)
подставим (1)




Структура фундаментальной системы решений (1) зависит от вида корней характеристического уравнения (3)
Случаи:1)
Все корни характеристического уравнения
(3) действительны и различны. Тогда
фундамент. Система примет вид:



2) Все корни характеристического уравнения (3) различны но среди них имеются комплексные:

Общее
решение (1):

Среди корней характеристического уравнения имеются кратные:


Пусть
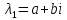 - к-краттный комплексный корень
следовательно
- к-краттный комплексный корень
следовательно также является к-кратным корнем. Разряд
кратностей = 2к.
также является к-кратным корнем. Разряд
кратностей = 2к.

15. Неоднородное линейное ду второго порядка с постоянными коэффициентами и специальной правой частью.

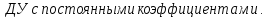
Построим частные решения уравнения (4)
f(x)=p(x)
Если
0 является то частное решение Q(x),
где Q(x)
многочлен той же степени что р(х) с
неопределенными коэф. Если 0 является
корнем причем кратности к, то

Если
 – не является корнем (3) то
– не является корнем (3) то ,
Если
,
Если – является корнем (3) то
– является корнем (3) то


16. Приложение линейных ду второго порядка. Свободные вынужденные колебания.
Рассмотрим прямолинейное движение материальной точки массы m по оси x. Пусть движение происходит по д действием 3-х сил.
1) Сила притяжения т.к. началу координат имеющая проекцию на Ох соответствует –ах, а> 0 .
2)
Сила сопротивления среды пропорциональна
1-й скорости соответствует

3)
Возмущающие силы направленные по оси
x
и F(t)
в момент времени t,
тогда применяя 2-й закон Ньютона получим
ДУ движения.
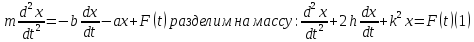
– НОЛУ 2-го порядка с постоянными коэффициентами.
Проинтегрировав кот. Найдем (решение x(t)) закон движения рассматриваемой точки. Представленное собой колебания в т. Х=0, то ур.(1) называется уравнением колебаний.
При
этом если сила отсутствует f(t)=0
то уравнение (1) примет вид:

– называется уравнением свободных колебаний. А если обратное то уравнением вынужденных колебаний.
Свободные колебания:
Т1
. Если h=0
колебания происходят в среде без
сопротивления тогда (2) примет вид:

Т2. h>0 колебания происходят в среде сопротивлений..
Характеристическое
уравнение:
Вынужденные колебания.
Т1.
Сила F(t)
периодическая и имеет синусоидальный
характер и колебания происходит в среде
без сопротивления, h=0:

T2.
Вынужденные колебания уравнения (1) в
среде с сопротивлением n<k
и возмущающаяся сила имеет синусоидальный
характер:




