4. Однородные ду.

Уравнение I-го порядка называется однородным если f(x,y) однородная функция своих аргументов нулевого измерения:

Предположим

Предположим

5. Линейное ду

Линейное ДУ I-го порядка называется ДУ вида:линейная относительно искомой функции и ее производной и А,В,С являются непрерывными функциями от Х. Делаем коэффициент =1

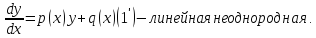
Способы решения

1. Метод вариации произвольной постоянной С.

Предполагает что общее решение (1’) имеет вид:

. После дифференциации(4) подставим в (4):

У(общее неоднородное) = у(общее однородное) + у(частное неоднородное)

2. Технический или метод Бернулли. Уравнение (1’) можно параметризировать используя подстановку Бернулли.

После решения мы получим общее решение которое совпадает с (5)

6. Уравнения Бернулли

Уравнение Бернулли которое можно проинтегрировать в замкнутом виде кадрирование и интегрирование сводится к линейному уравнению.

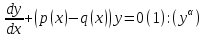
Решение (5) подставить в (3) извлечем корень и получим общее решение (1)

7. Ду в полных дифференциалах.

Уравнение вида: 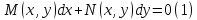называется уравнение в полных дифференциалах если его левая часть является полным дифференциалом искомой функцииu(x,y).

Для того чтобы уравнение (1) было уравнением в полных дифференциалах необходимо и достаточно чтобы выполнялось: (3)

Доказательство основывается на том что из уравнения (2) должны иметь следующие соотношения:

Чтобы найти

Интегральным множителем для уравнения (1) называется такая функция , которая при умножении на каждое уравнение (1) превращается в уравнение в полных дифференциалах .

8. Теорема существования и единственности решения ду I-го порядка.

Точка 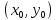называется неособой если существует ее окр.U т.ч. через точку этой окрестности проходит интегральная кривая причем только одна, в противном случае эта точка называется особой.

Решение всех точек которые особые называется особое решение.

1) Пусть f(x,y) непрерывная функция двух переменных в замкнутой области R:

т.к. непрерывная функция в замкнутой области является ограниченной следовательно

2) Функция f(x,y) удовлетворяет условию ЛИПНЕЦА :

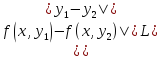
Теорема. Если f(x,y) непрерывна на R и удовлетворяет условию ЛИПНИЦА то задача Каши (1) имеет единственное решение определенная и непрерывная для значенийx в интервале

принимает при 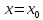значение.

9. Ду высших порядков которые интегрируются в квадратурах

1 тип:

II – тип. Уравнения содержащие две последовательных производных:

III- тип. Уравнения содержащие n и n-2 производную

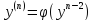
IV – тип

-эта подстановка сводит ур-е 6-го типа к ур-ю (n-k)-го порядка:

Если (14) интегрируется в квадратурах,т.что … ,,то подставляя в (13)получим:

V-тип.

VI- тип. Однородное ДУ относительно если удовлетворяет:

VII-тип. Уравнения точных производных

11. Теорема существования и единственности для системы линейных ду и для линейного ду n-го порядка (без док-ва).

Рассмотрим систему лин. ДУ вида: (1),. Система (1) задана в нормальной форме:– неизв.- изв. функция. Обозначим:, Тогда система (1) примет вид:(1'). Зададим начальное условие(2) и сформул. задачу Коши: найти решение (1') удовл. нач. условию (2).. Теорема. Пусть вектор функция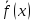и матрица функции A(x) непрерывно на некотором отрезке [a,b], тогда. 1. решение задачи Коши (1'), (2) существ. на всем отрезке и большое; 2. это решение единственно на I (если существ.,- на I следовательно) Замечание! В отличии от теоремы (сущ. и един.) для нелинейных систем эта теорема глобальная, т.к. решение существ. и единственно на всем отрезке I.