4.5. Трансформатор без стального сердечника (воздушный трансформатор)

В электротехнике широкое применение имеет трансформатор – аппарат, предназначенный для преобразования переменного напряжения. В простейшем случае он не имеет ферромагнитного сердечника и представляет собой две катушки с индуктивной связью (рис. 4.11). Такие трансформаторы применяются при

высоких частотах, а в некоторых специальных измерительных устройствах и при низких частотах синусоидального тока.

О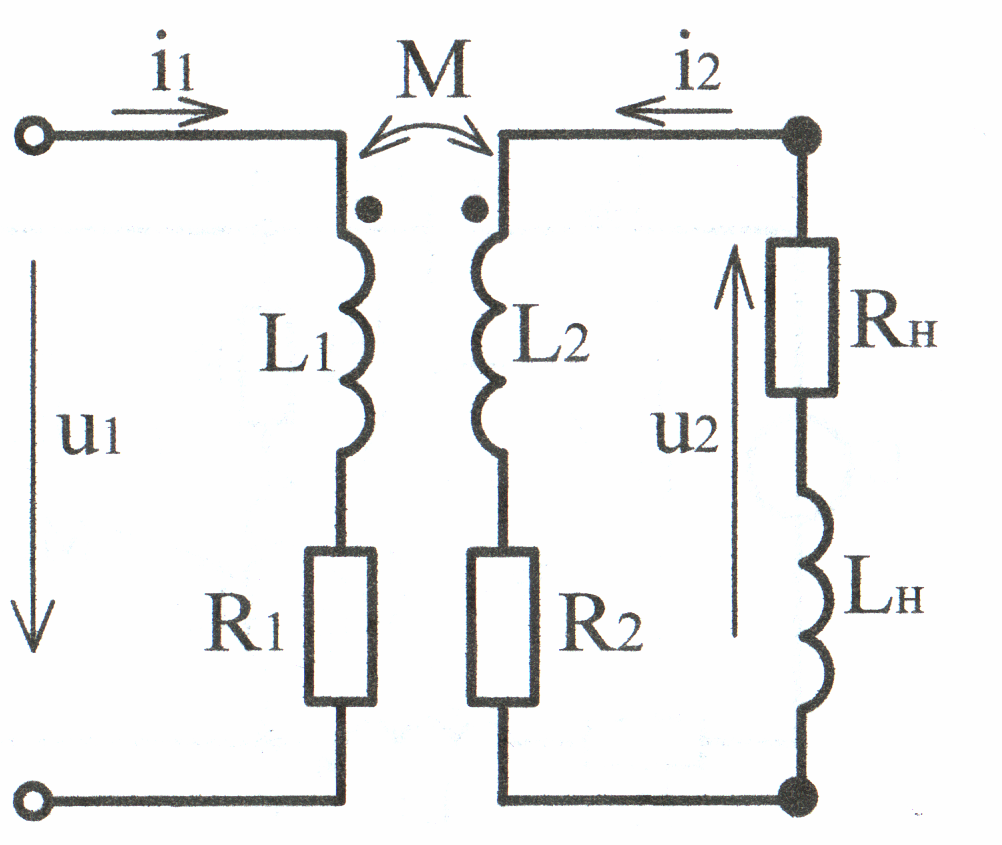 бмотка трансформатора с параметрами , , к которой подключается источник питания, называется

первичной; обмотка с

параметрами , , к которой

присоединяется приёмник энергии (нагрузка) с параметрами , , называется вторичной. Напряжения между

Рис. 4.11 зажимами обмоток и токи в

этих обмотках называются

соответственно первичными u₁, i₁ и вторичными u₂, i₂ напряжениями и токами трансформатора. Цепи, в состав которых входят первичные и вторичные обмотки трансформатора называются соответственно первичными и вторичными цепями трансформатора. Составим уравнения для мгновенных значений токов и напряжений по второму закону Кирхгофа для первичной и вторичной цепей трансформатора (при указанных на рис. 4.11 одноименных зажимах и направлениях токов магнитные потоки самоиндукции и взаимной индукции имеют одинаковые направления и суммируются):

; (4.31)

; (4.32)

где  вторичное напряжение трансформатора (напряжение на приёмнике).

Перейдём от уравнений в классической форме трансформатора (4.31), (4.32) к уравнениям в комплексной форме:

, (4.33)

, (4.34)

где ,  индуктивные сопротивления первичной и вторичной обмоток;  сопротивление взаимной индукции обмоток;

; .

Взаимная индуктивность M, входящая в уравнения (4.31)   (4.34), определяется из режима холостого хода трансформатора (при ). Для холостого хода вторичное напряжение из уравнения (4.34)

,

откуда . (4.35)

Обозначим через и .

Решая уравнения (4.33) и (4.34) относительно тока , получаем:

, (4.36)

где 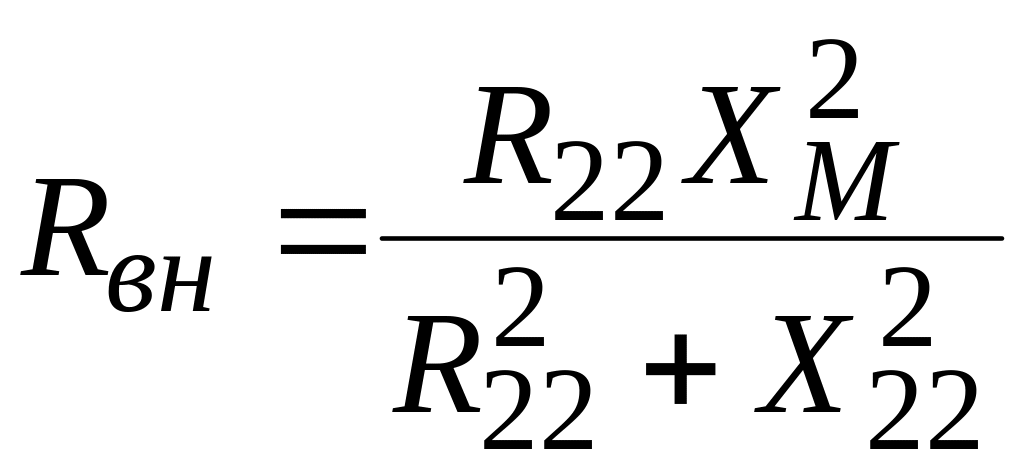; (4.37)

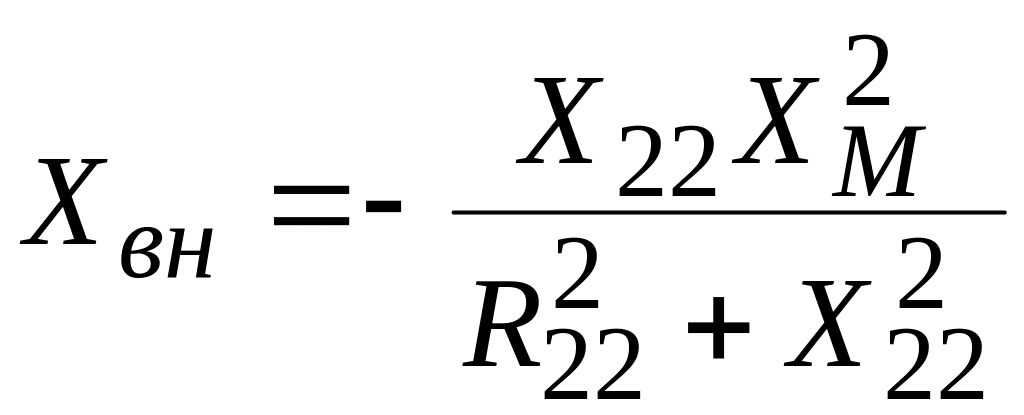, (4.38)

сопротивления и называют вносимыми активным и реактивным сопротивлениями (они вносятся магнитным полем из вторичной цепи трансформатора в первичную цепь).

И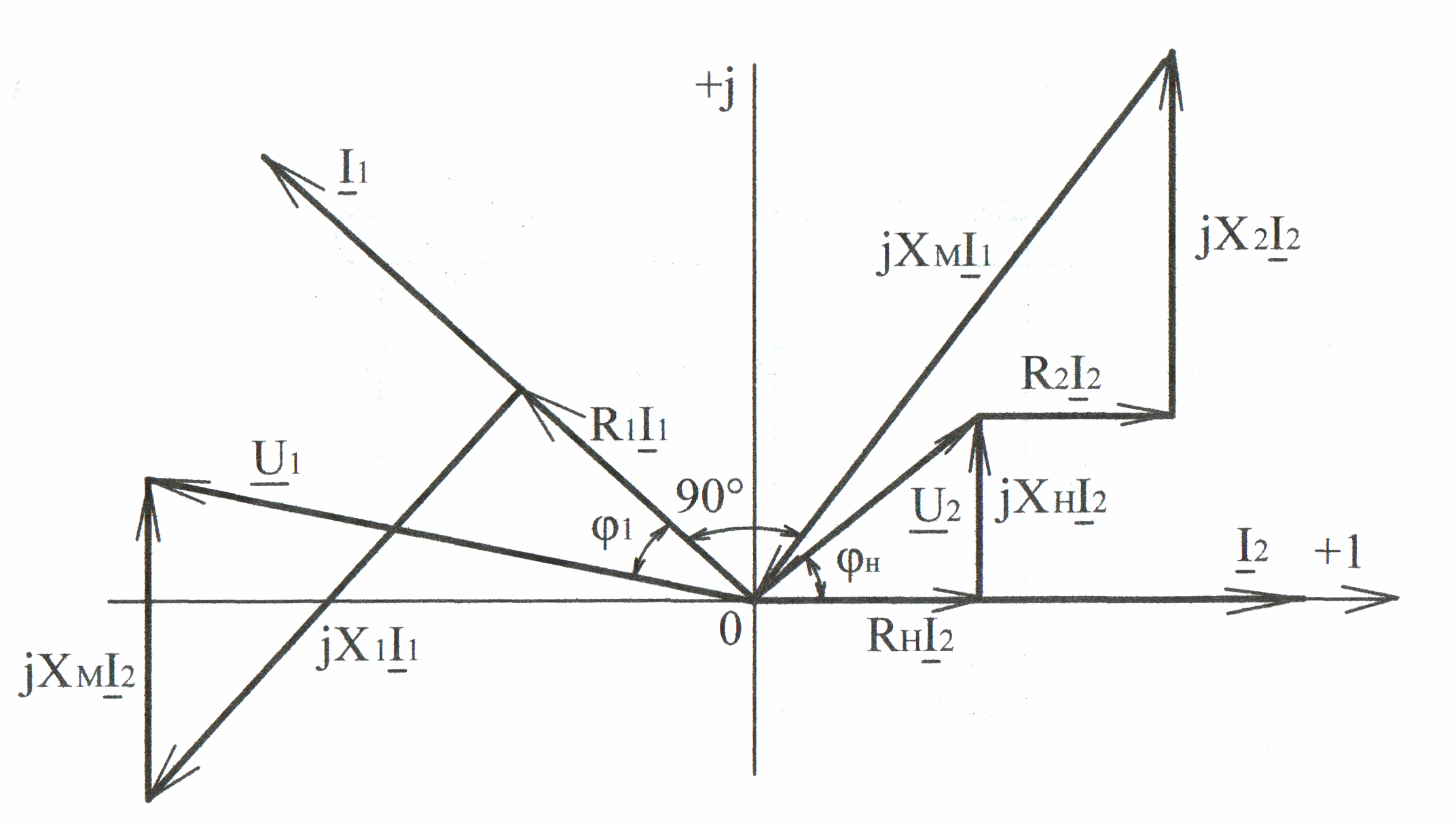 з структуры выражения (4.36) следует, что со стороны первичной цепи воздушного трансформатора вся схема может рассматриваться как двухполюсник с сопротивлениями и . Таким образом, наличие вторичной цепи эквивалентно изменению активного и реактивного сопротивлений двухполюсника на и . Вносимое активное сопротивление всегда больше нуля. В нём поглощается энергия, которая передаётся из первичной цепи во вторичную посредством

Рис. 4.12

магнитного поля. Вносимое реактивное сопротивление имеет знак, противоположный знаку Х₂₂.

На основании уравнений (4.33) и (4.34) построим векторную диаграмму воздушного трансформатора для индуктивного характера нагрузки (рис. 4.11).

За исходный вектор принимаем , который направляем по оси вещественных величин (рис. 4.12). Затем строим треугольник активного , индуктивного и полного напряжений нагрузки. Из конца вектора откладываем векторы активного и индуктивного напряжений вторичной обмотки трансформатора. В соответствии с уравнением (4.34) сумма всех комплексных напряжений вторичной цепи равна нулю. Поэтому вектор напряжения взаимной индукции вторичной обмотки будет направлен в начало координат, т. е. образуется замкнутый многоугольник напряжений вторичной цепи. Далее, из начала координат под углом 90 к вектору (вектор при согласном включении катушек опережает вектор тока на угол 90) проводим вектор . Вектор активного напряжения первичной обмотки совпадает с вектором , а индуктивного напряжения  опережает на 90. Вектор напряжения взаимной индукции первичной обмотки опережает вектор вторичного тока на угол 90. В соответствии с уравнением (4.33) вектор входного напряжения первичной цепи равен сумме трёх векторов составляющих напряжений.

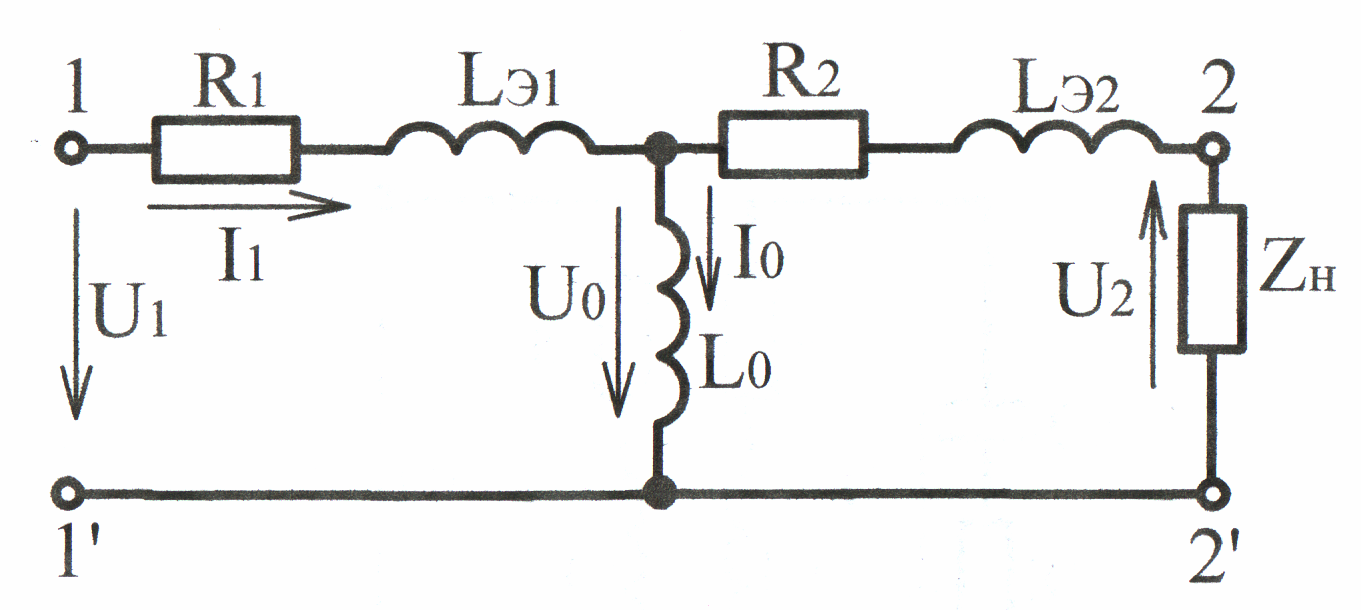
Схема воздушного трансформатора (рис. 4.11), т. е. схема с индуктивной связью катушек может быть заменена эквивалентной схемой (рис. 4.13) без индуктивной связи.

I₂

Рис. 4.13

Эквивалентные индуктивности схемы (рис. 4.13):

; ; . (4.39)

Для этой схемы, учитывая, что , имеем следующие уравнения для двух контуров по второму закону Кирхгофа.

Для левого контура:

;

или после сокращения, получим:

.

Для правого контура:

;

раскроем скобку и заменим :

;

после сокращения, получим:

.

Полученные уравнения для схемы (рис. 4.13) совпадают с уравнениями (4.33) и (4.34), следовательно, эта схема эквивалентна воздушному трансформатору.

Воздушный трансформатор называется идеальным, если при любых условиях отношение первичного и вторичного комплексных напряжений и отношение вторичного и первичного комплексных токов равны друг другу и равны постоянному комплексному числу :

. (4.40)

Это комплексное число называется коэффициентом трансформации идеального трансформатора. Чтобы выполнить соотношения (4.40) необходимо выполнение следующих условий:

1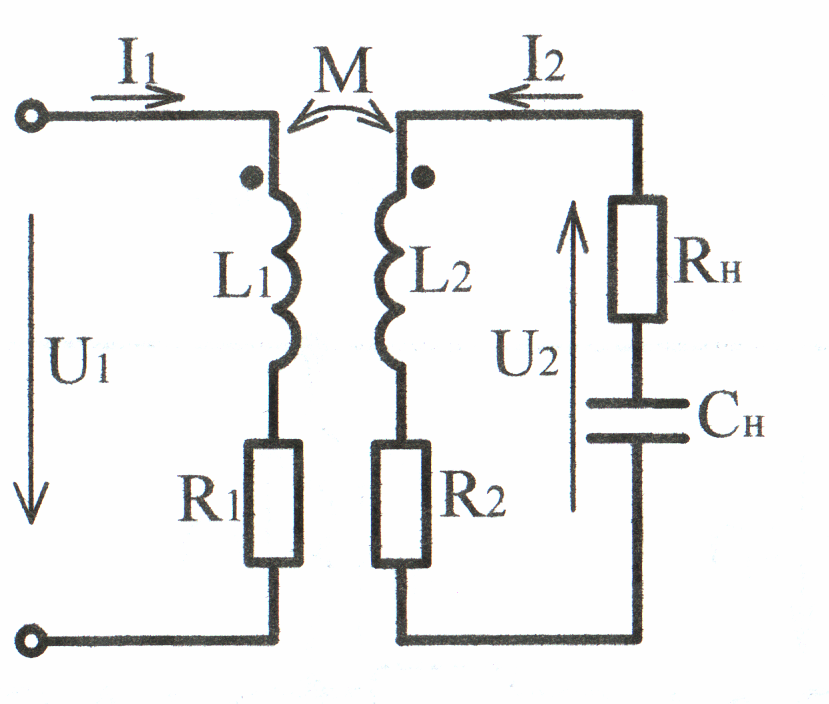 ) Активные сопротивления первичной и вторичной обмоток трансформатора должны быть равны нулю;

2) Коэффициент магнитной связи между обмотками должен быть равен единице ( ).

Пример 4.1. Рассчитать воздушный трансформатор (рис.4.14) при частоте Гц,

Рис. 4.14 если заданы параметры катушек

и нагрузки, а также ток

вторичной цепи: Ом; Гн; Ом;

Гн; М = 0,178 Гн; Ом; мкФ;

А.

Определить:

1) Коэффициент магнитной связи катушек;

2) Напряжение и ток первичной цепи, напряжение вторичной цепи;

3) Вносимые активное и реактивное сопротивления;

4) Активные мощности первичной и вторичной обмоток и нагрузки . Активную и реактивную мощности источника энергии.

Построить по результатам расчёта векторную диаграмму воздушного трансформатора.

Р е ш е н и е. Угловая частота переменного тока

с^-1.

Реактивные сопротивления обмоток и нагрузки:

Ом;

Ом;

Ом;

Ом.

Коэффициент магнитной связи катушек:

.

Напряжение вторичной цепи:

, В.

Из уравнения (4.34) определяем ток первичной цепи:

;

, А.

Таким образом, ток первичной цепи А, а его начальная фаза .

Напряжение первичной цепи определяем из уравнения (4.33):

, В.

Следовательно, напряжение первичной цепи воздушного трансформатора В, а его начальная фаза .

Вносимое активное сопротивление определяем по формуле (4.37):

Ом;

Ом,

здесь взято со знаком «минус», так как оно является емкостным сопротивлением.

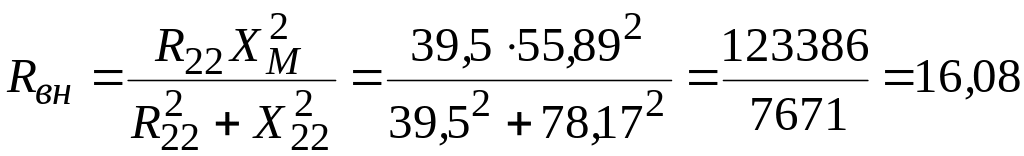Ом.

Вносимое реактивное сопротивление определяем по формуле (4.38):

Ом.

Для проверки определим первичный ток по формуле (4.36):

, А.

Сравнивая полученное выражение комплекса тока с ранее вычисленным значением, видим, что модуль и аргумент комплекса практически совпали.

Потери активной мощности в первичной обмотке

Вт;

Потери активной мощности во вторичной обмотке

Вт;

Активная мощность нагрузки

Вт.

Комплексная мощность источника энергии

;

таким образом, активная мощность источника энергии Р = 14,79 Вт, а реактивная Q = 6,48 вар.

Баланс активных мощностей для воздушного трансформатора:

Вт.

Наличие баланса активных мощностей подтверждает правильность решения задачи.

Для построения векторной диаграммы воздушного трансформатора вычислим составляющие напряжений вторичной и первичной цепей в комплексной форме.

В; , В;

В;

, В;

, В;

, В;

, В;

, В.

Вектор тока направляем по оси вещественных величин (рис. 4.15). Активное напряжение нагрузки совпадает с , а емкостное напряжение нагрузки отстаёт от на угол 90.

Вектор вторичного напряжения трансформатора соединяет начало вектора и конец вектора . Из конца вектора проводим параллельно вектор активного напряжения вторичной обмотки ; индуктивное напряжение опережает на 90. Многоугольник напряжений вторичной цепи замыкает вектор напряжения взаимной индукции этой цепи . Под углом 90 к вектору в сторону отставания от него проводим вектор

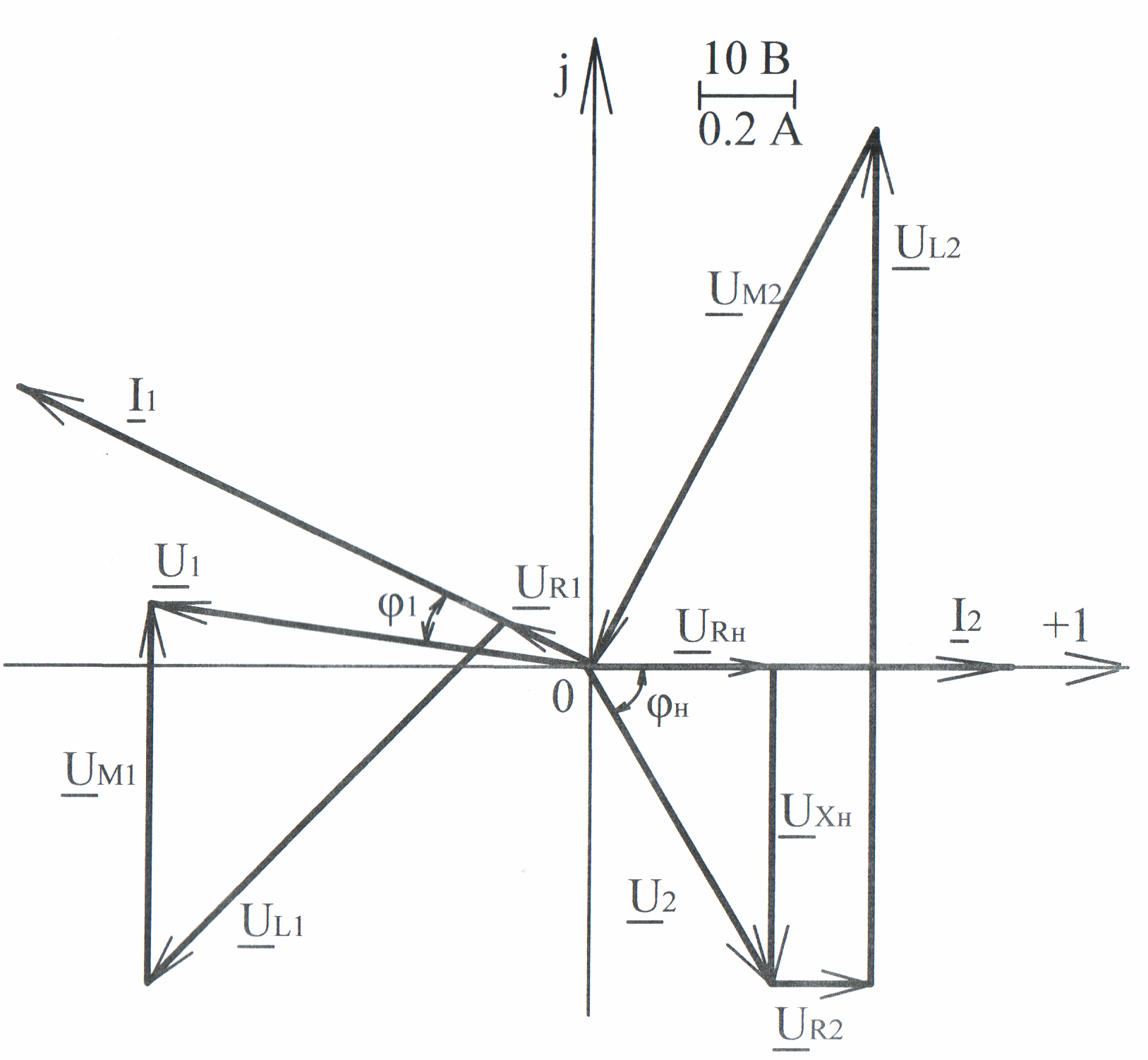
Рис. 4.15

тока первичной цепи . Активное напряжение первичной обмотки совпадает по фазе с , а индуктивное напряжение опережает на 90. Напряжение взаимной индукции первичной цепи опережает вектор на 90. Вектор напряжения первичной цепи опережает ток на угол .

23