
лекции / DSP_13
.pdf
1
Лекция 13. Быстрое преобразование Фурье (БПФ)
1.БПФ Кули-Тьюки.
2.Одноэтапный алгоритм БПФ.
3.Двухэтапный алгоритм БПФ.
4.ν-этапныйй алгоритм БПФ.
5.Эффективность алгоритма БПФ.
6.Формирование начальных условий в алгоритме БПФ.
7.Вычисление ОДПФ с помощью БПФ.
13.1. БПФ Кули-Тьюки
Рассмотрим, какое количество арифметических операций с комплексными числами требуется для вычисления ДПФ (12.17):
|
|
N 1 |
|
|
|
|
|
|
X(k) x(n)WNnk, |
k 0,1,..., N 1, |
(12.17) |
||||
|
|
n 0 |
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
Wnk |
|
j |
2 |
nk |
|
|
|
e |
|
N . |
(12.19) |
||
|
|
N |
|
|
|
|
|
Вычисление X(k) |
представляет собой цикл в цикле: внутренний цикл по n, внешний |
||||||
по k. |
|
|
|
|
|
|
|
Для внутреннего цикла: |
|
|
|
|
|
|
|
k fix; n 0, ... , |
N 1 |
N 1 N |
|
||||
|
|
|
2N операций. |
|
|||
|
|
N |
|
|
|
|
|
При k 0,1, ..., N 1 2N N 2N2 |
операций. |
|
|||||
Порядок вычислительной сложности относительно длины последовательности N:
O(N2).
БПФ — это совокупность алгоритмов, предназначенных для быстрого вычисления ДПФ.
Первый БПФ Кули-Тьюки (БПФ по основанию 2) опубликован в 1965 г., в нем длина исходной последовательности должна быть степенью двойки:
N 2 |
. |
(13.1) |
Если длина N не удовлетворяет условию (13.1), последовательность дополняется нулями.
Основная идея — поэтапное (циклическое) вычисление ДПФ через ДПФ вдвое меньшей последовательности. Всего этапов.
13.2. Одноэтапный алгоритм БПФ
Начальные условия алгоритма: исходную N-точечную последовательность разделим на две N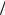 2-точечные (рис. 13.1 и 13.2):
2-точечные (рис. 13.1 и 13.2):
четных отсчетов;
нечетных отсчетов.
Получили группу «чет N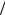 2 + неч N
2 + неч N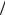 2», которую используем для расчета N-
2», которую используем для расчета N-
точечного ДПФ.
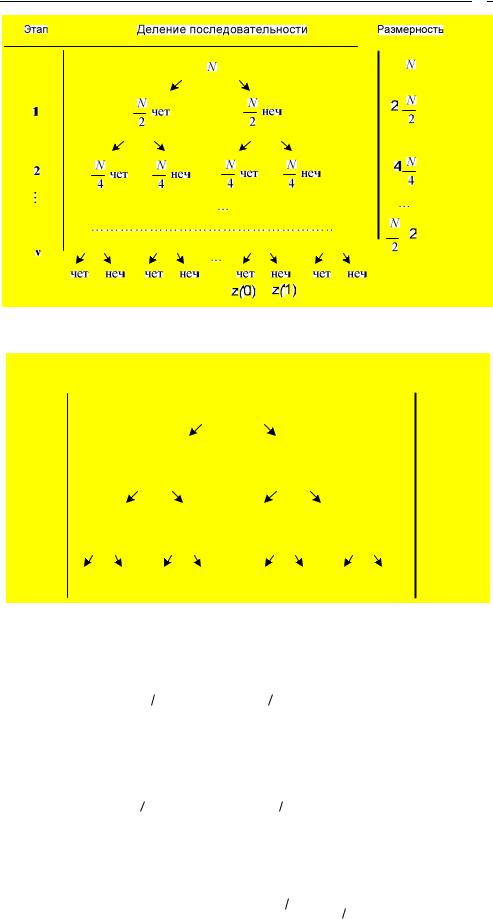
2
Рис. 13.1. Деление исходной последовательности
Этап |
Деление 8-точечной |
Размерность |
||
последовательности |
||||
|
|
|||
|
x(0) x(1) x(2) x(3) x(4) x(5) x(6) x(7) |
8 |
||
1 |
x(0) x(2) x(4) x(6) |
x(1) x(3) x(5) x(7) |
2*4 |
|
2 |
x(0) x(4) |
x(2) x(6) |
x(1) x(5) |
x(3) x(7) |
4*2 |
3
x(0) |
x(4) |
x(2) |
x(6) |
x(1) |
x(5) |
x(3) |
x(7) |
Рис. 13.2. Пример деления 8-точечной последовательности
Вывод формулы БПФ
С учетом начальных условий ДПФ (12.17) примет вид:
|
N 2 1 |
N 2 1 |
X(k) |
x(2n)WN(2n)k |
x(2n 1)WN(2n 1)k |
|
n 0 |
n 0 |
где (2n) отображает четные, а (2n 1) — нечетные значения n.
Вынесем Wk |
за знак второй суммы: |
|
|
|
|
||||
N |
|
|
|
|
|
|
|
|
|
|
|
N 2 1 |
|
|
|
|
N 2 1 |
||
|
X(k) |
x(2n)WN(2n)k WNk |
|
x(2n 1)WN(2n)k |
|||||
|
|
n 0 |
|
|
|
|
|
n 0 |
|
представим WN(2n)k в виде: |
|
|
|
|
|
|
|
||
|
|
|
j |
2 |
2nk |
j |
2 |
nk |
|
|
|
W2nk |
|
||||||
|
|
e N |
e |
|
N 2 Wnk |
||||
|
|
N |
|
|
|
|
|
|
N 2 |
,
,(13.2)
и запишем ДПФ (13.2):

3
|
|
|
N 2 1 |
N 2 1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
X(k) x(2n)WNnk2 WNk |
|
x(2n 1)WNnk2 , |
|
k 0,1, ..., N 1, |
|
|||||||||||
|
|
|
n 0 |
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
X0(k) |
|
|
|
|
|
X1(k) |
|
|
|
|
|
|
|||
или коротко: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
X(k) X0(k) WNk X1(k) , |
k 0,1, ..., N 1, |
|
(13.3) |
||||||||||||
где: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X0(k) — N/2-точечные ДПФ четных отсчетов; |
|
|
|
|
|
|
|
|
|
|||||||||
X1(k) — N/2-точечные ДПФ нечетных отсчетов. |
|
|
|
|
|
|
||||||||||||
С учетом периодичности ДПФ X0(k) и X1(k) |
справедливы равенства: |
|
||||||||||||||||
|
|
|
|
N |
k 0,1,..., |
|
N |
|
|
|
|
|
|
|||||
|
|
|
X0(k) X0 k |
|
|
|
, |
|
|
|
1; |
|
(13.4) |
|||||
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
N |
k 0,1,..., |
N |
|
|
|
|
|
|
|||||
|
|
|
X1(k) X1 k |
|
|
, |
|
|
1. |
|
(13.5) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
||||
Вывод: при вычислении N-точечного ДПФ |
X(k) (13.3) ДПФ |
X0(k) и |
X1(k) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
достаточно |
вычислить на первой |
половине |
периода |
|
0; |
|
1 , а на |
второй |
||||||||||
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; N 1 |
— продублировать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим поворачивающей множитель на второй половине периода :
|
N |
|
N |
|
|
2 |
|
N |
|
|
|
|
k |
|
|
|
Wke |
j |
|
Wke j Wk . |
(13.6) |
||||
|
||||||||||||
W |
2 |
WkW 2 |
|
N 2 |
||||||||
N |
|
N |
N |
N |
|
|
|
|
N |
N |
|
|
Вывод: поворачивающий множитель WNk достаточно вычислить на первой половине
периода N , а на второй — изменить знак.
2
Это позволяет заменить последовательное вычисление N-точечного ДПФ в (13.3) параллельным вычислением через N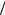 2-точечные ДПФ (рис. 13.3).
2-точечные ДПФ (рис. 13.3).
X(k) X |
0 |
(k) Wk |
X |
(k) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
N |
1 |
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
||||
X |
|
k |
|
|
X |
0 |
(k) W |
N |
X |
1 |
(k) |
(13.7) |
|||||
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k 0,1, ..., |
|
|
1, |
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Согласно (13.7), одновременно вычисляются следующие отсчеты ДПФ:
N
при k 0 X(0) и X ;
2
при k 1 X(1) |
и X |
|
|
N |
|
|
||||||
|
|
|
1 |
; |
||||||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
||||
……………………………. |
|
|
||||||||||
при k |
N |
N |
|
|
|
и X(N 1) . |
||||||
|
1 |
X |
|
|
|
1 |
||||||
2 |
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|||
В (13.7) размерность вычисляемого ДПФ соответствует нижнему индексу WNk .

4
Выигрыш в количестве арифметических операций определим позже для полного υ- этапного алгоритма. Пока отметим, что это оказалось возможным благодаря делению исходной последовательности на четные и нечетные отсчеты.
Pазмерность |
|
|
|
|
Этап |
|||||||
|
ДПФ |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
N |
|
|
|
X |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
N |
|
|
|
X0 |
X1 |
|
ν 1 |
||
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
||||
4 |
N |
|
|
X00 |
X01 |
X10 |
X11 |
|
||||
|
|
|
|
|||||||||
4 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
……………………………... |
|
|
||
|
N |
|
|
|
|
|
Z(0) |
Z(1) |
|
|
||
|
2 |
|
|
…. |
…… |
|
1 |
|||||
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
z(0) z(1)
Начальные условия
Рис. 13.3. Поэтапное вычисление N-точечного ДПФ
Параллельное вычисление в (13.7) при фиксированном k называют операцией «бабочка» и изображают в виде сигнального графа (рис. 13.4).
X0(k) |
|
X(k) X |
0 |
(k) Wk X |
(k) |
|
|||
|
|
|
|
|
|
N 1 |
|
|
|
|
Wk |
|
|
|
|
|
|
||
|
N |
N |
|
|
|
||||
X1(k) |
|
|
|
k |
|
||||
|
X k |
|
|
|
X0(k) WN |
X1(k) |
|||
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
||
|
|
|
|
||||||
k 0,1,..., N 1 2
Рис. 13.4. Сигнальный граф операции «бабочка»
Для вычисления N-точечного ДПФ по формуле (13.7) требуется N «бабочек».
2
13.3. Двухэтапный алгоритм БПФ
Начальные условия алгоритма: каждую из N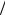 2-точечных последовательностей разделим на две N
2-точечных последовательностей разделим на две N 4-точечные (рис. 13.1—13.2):
4-точечные (рис. 13.1—13.2):
четных отсчетов (в порядке следования, считая от нуля);
нечетных отсчетов (в порядке следования, считая от нуля).
Получили две группы «чет N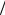 4 + неч N
4 + неч N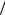 4».
4».
Используем их для расчета двух N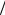 2-точечных ДПФ X0(k) и X1(k) через N
2-точечных ДПФ X0(k) и X1(k) через N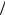 4- точечные ДПФ по формуле (13.7).
4- точечные ДПФ по формуле (13.7).
Это первый этап двухэтапного алгоритма.
Количество формул увеличилось вдвое, а размерность ДПФ в каждой из них вдвое уменьшилась.

5
Обозначим:
X00(k) и X01(k) — N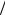 4-точечные ДПФ четных и нечетных отсчетов в первой группе;
4-точечные ДПФ четных и нечетных отсчетов в первой группе;
X00(k) и X01(k) — N 4-точечные ДПФ четных и нечетных отсчетов во
4-точечные ДПФ четных и нечетных отсчетов во
второй группе;
Формулы (13.7) примут вид:
X |
|
(k) X |
|
(k) Wk |
|
|
X |
|
|
(k) |
|
|
|
|
(13.8) |
|||
|
0 |
|
|
00 |
|
N |
/2 |
|
|
01 |
k |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X0 |
k N /4 X00(k) WN /2X01(k) |
|
|
|||||||||||||||
k 0,1,...,N /4 1, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
(k) X |
|
|
(k) Wk |
|
X |
|
|
(k) |
|
|
|
|
(13.9) |
||||
|
1 |
|
10 |
|
N |
/2 |
|
|
11 |
|
k |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(k) |
|
|
|||
X1 |
k N /4 X10(k) WN /2X11 |
|
|
|||||||||||||||
k 0,1, ...,N /4 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Размерность вычисляемого ДПФ соответствует нижнему индексу Wk |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
/2 |
|
|
На первом этапе для вычисления ДПФ X0(k) |
и X1(k) требуется |
N |
«бабочек». |
|||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Второй этап (рис. 13.3): вычисление N-точечного ДПФ |
|
X(k) |
через |
N 2-точечные |
||||||||||||||
ДПФ X0(k) и X1(k) по формуле (13.7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
13.4. ν-этапныйй алгоритм БПФ
Рассмотренную закономерность легко распространить на на трехэтапный алгоритм БПФ:
начальные условия: каждая из N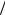 4-точечных последовательностей делится
4-точечных последовательностей делится
на две «чет N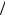 8 + неч N
8 + неч N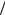 8» и таких групп четыре;
8» и таких групп четыре;
первый этап — расчет N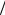 4-точечных ДПФ через N
4-точечных ДПФ через N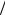 8-точечные ДПФ с использованием четырех формул типа (13.7).
8-точечные ДПФ с использованием четырех формул типа (13.7).
второй этап — расчет N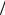 2-точечных ДПФ через N
2-точечных ДПФ через N 4-точечные ДПФ с использованием двух формул типа (13.7).
4-точечные ДПФ с использованием двух формул типа (13.7).
третий этап — расчет N-точечного ДПФ через N 2-точечные ДПФ по формуле
2-точечные ДПФ по формуле
(13.7).
И т. д.
Процесс деления исходной последовательности на чет и нечет можно продолжить до тех пор, пока в группе не останется два отсчета — один чет, второй — нечет.
Получим N групп 2-точечных последовательностей. Это начальные условия -
2
этапного алгоритма БПФ (рис. 13.1—13.2).
Первый этап — особенный, т. к. на этом этапе вычисляются N 2-точечных ДПФ
2
непосредственно по 2-точечным последовательностям (рис. 13.4). Для этого
требуется N формул типа (13.7).
2
Запишем одну из них, используя условные обозначения: z(0) и z(1) — четный и
нечетный отсчеты последовательности; Z(0) и Z(1) |
— отсчеты 2-точечного ДПФ: |
|
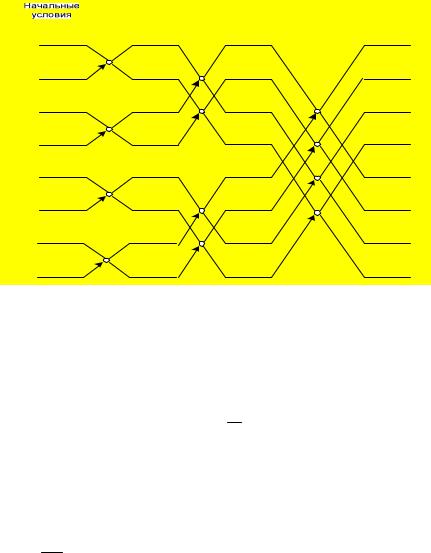
Z(k) z(0) Wkz(1) |
(13.10) |
|
|
2 |
|
Z(k 1) z(0) W2kz(1)
k 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
На первом этапе выполняется |
N |
«бабочек». |
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
втором |
этапе — расчет |
|
N |
|
4-точечных |
ДПФ через |
2-точечные ДПФ |
|
с |
|||||
4 |
|
|
|
||||||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|||
использованием |
формул типа (13.7). и т. д. (рис. 13.3). |
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
каждом |
этапе выполняется |
N |
«бабочек». |
Сигнальный |
граф алгоритма |
8- |
||||||||
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
точечного БПФ представлен на рис. 13.5.
x(0) |
|
|
X (0) |
W20 |
|
|
|
|
|
|
|
x(4) |
W40 |
|
X (1) |
|
|
|
|
x(2) |
1 |
W 0 |
X (2) |
W4 |
8 |
||
|
W20 |
W1 |
|
|
|
X (3) |
|
x(6) |
|
8 |
|
|
|
|
|
|
|
W 2 |
X (4) |
x(1) |
W20 |
8 |
|
|
|
||
|
|
|
|
x(5) |
W 0 |
W 3 |
X (5) |
4 |
8 |
|
|
x(3) |
W41 |
|
X (6) |
W20 |
|
|
|
|
|
|
X (7)
x(7)
Рис. 13.3. Сигнальный граф 8-точечного БПФ
13.5. Эффективность алгоритма БПФ
Определим количество арифметических операций с комплексными числами в БПФ:
количество этапов — log2 N ;
количество бабочек на каждом этапе — N ;
2
количество арифметических операций с комплексными числами для одной бабочки:
2
3
1
ИТОГО — 3N log2 N операций.
2
Порядок вычислительной сложности относительно длины последовательности N:
O(Nlog2 N) .
Выигрыш в количестве операции по сравнению с ДПФ для N 1024 в 100 раз и он возрастает с ростом длины N.
13.6. Формирование начальных условий в алгоритме БПФ
Начальную расстановку отсчетов исходной последовательности в -этапном алгоритме БПФ называют прореживании последовательности.
Рассмотрим алгоритм прореживания последовательности на примере 8-точечного БПФ (рис. 13.2) и результаты обобщим.

7
Исходная последовательность |
Прореженная последовательность для БПФ |
|||
|
|
|
|
|
Отсчет |
Двоичный номер |
Двоичный номер |
Отсчет |
|
отсчета |
отсчета |
|||
|
|
|||
|
|
|
|
|
x(0) |
000 |
000 |
x(0) |
|
|
|
|
|
|
x(1) |
001 |
100 |
x(4) |
|
|
|
|
|
|
x(2) |
010 |
010 |
x(2) |
|
|
|
|
|
|
x(3) |
011 |
110 |
x(6) |
|
|
|
|
|
|
x(4) |
100 |
001 |
x(1) |
|
|
|
|
|
|
x(5) |
101 |
101 |
x(5) |
|
|
|
|
|
|
x(6) |
110 |
011 |
x(3) |
|
|
|
|
|
|
x(7) |
111 |
111 |
x(7) |
|
|
|
|
|
|
Вывод: Для алгоритма БПФ отсчеты исходной последовательности должны быть расставлены в бит-реверсивной последовательности своих двоичных номеров.
13.7. Вычисление ОДПФ с помощью БПФ
ОДПФ (12.18):
1 |
N 1 |
|
|
x(n) |
|
X(k)WNnk, n 0,1, ..., N 1. |
(12.18) |
|
|||
|
N k 0 |
|
|
Алгоритм вычисления ОДПФ (12.18) с помощью БПФ включает в себя следующие шаги:
обе части равенства умножаются на N и выполняется операция их комплексного сопряжения (символ *):
|
N 1 |
|
Nx (n) X (k)WNnk ; |
|
k 0 |
правая часть |
равенства — N-точечное ДПФ последовательности X (k) |
вычисляется с |
помощью БПФ; |
выполняется операция комплексного сопряжения обеих частей полученного равенства с делением на N :
|
1 N 1 |
|
|
|
|
|
|||
x(n) |
|
X (k)WNnk |
|
, n 0,1, ..., N 1. |
|
||||
|
N |
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
