лекции / DSP_10
.pdf
1
Лекции 10. Синтез БИХ-фильтров
1.Синтез БИХ-фильтров на основе АФП.
2.Метод инвариантности импульсной характеристики.
3.Метод билинейного Z-преобразования.
4.Свойства билинейного Z-преобразования.
5.Процедура синтеза БИХ-фильтра методом билинейного Z-преобразования.
10.1. Синтез БИХ-фильтров на основе АФП
Синтез БИХ-фильтров на основе аналоговых фильтров-прототипов (АФП) основан на том, что передаточные функции БИХ-фильтра H(z) и АФП H(p) имеют одинаковое математическое представление в виде:
дробно-рациональной функции;
произведения передаточных функций биквадратных звеньев;
суммы передаточных функций звеньев 2-го порядка.
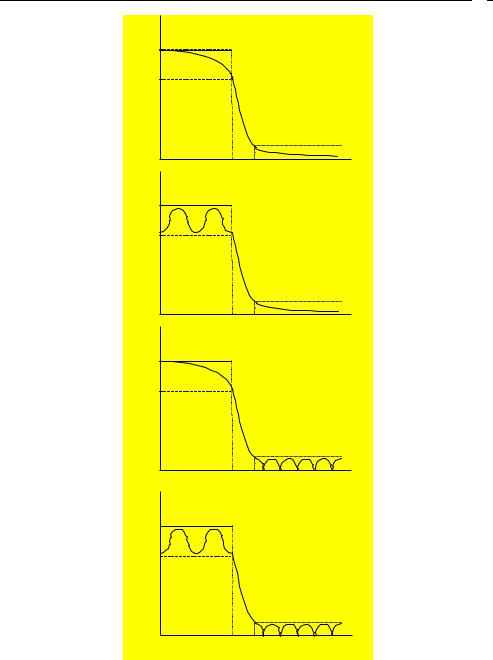
По виду аппроксимирующей функции различают четыре типа АФП и БИХ-фильтра
(рис.10.1):
Баттерворта (Butterwhorth) — с АЧХ, максимально плоской в ПП и монотонной в ПЗ;
Чебышева I рода (Chebyshev Type I) — с АЧХ, равноволновой в ПП и монотонной в ПЗ;
Чебышева II рода (Chebyshev Type II) — с АЧХ, максимально плоской в ПП и равноволновой в ПЗ;
Золотарева—Кауэра (Elliptic — эллиптический) — с АЧХ, равноволновой в
ППи ПЗ.
2
A( ) 1
0 |
|
|
k |
|
|
A( ) |
|
1 |
|
0 |
|
|
k |
|
|
A( ) |
|
1 |
|
0 |
|
|
|
|
|
|
k |
|
A( ) |
|
|
1 |
|
|
0 |
|
|
|
k |
|
|
|
|
Рис. 10.1. Приблизительный вид АЧХ АФП (для ФНЧ): Баттерворта; Чебышева 1-го рода; Чебышева 2-го рода; Золотарева-Кауэра
10.2. Метод инвариантности импульсной характеристики
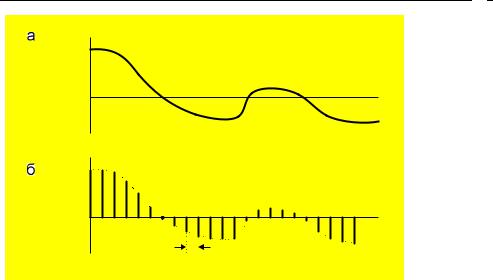
Постановка задачи: синтезировать БИХ-фильтр, ИХ которого совпадает с ИХ АФП в дискретных точках (рис. 10.2):
h(nT) h(t) |
|
t nT |
. |
(10.1) |
|
Под термином «инвариантность ИХ» понимают неизменность ИХ при изменении типа фильтра АФП/БИХ-фильтр (с учетом (10.1)).
3
h(t)
0 |
t |
h(nT)
0 |
|
nT |
|
|
|
|
|
|
|
|
T |
Рис. 10.2. Импульсная характеристика: АФП (а); ЦФ (б)
Синтез БИХ-фильтра заключается в расчете передаточной функции H(z) .
Следовательно, решение задачи сводится к определению неизвестной передаточной функции БИХ-фильтра H(z) по известной передаточной функции АФП H(p) при условии инвариантности их импульсных характеристик.
С этой целью выполним следующие действия: |
|
выразим передаточную функцию БИХ-фильтра через его ИХ h(nT) |
(см. (4.1)): |
|
|
H(z) h(nT)z n ; |
(10.2) |
n 0 |
|
определим ИХ АФП h(t) по известной передаточной функции H(p) :
По определению ИХ h(t) есть обратное преобразование Лапласа передаточной функции H(p) :
h(t) L 1 H(p) .
Представим H(p) |
в виде суммы простых дробей: |
|
|
|||||||
|
|
|
M 1 A |
|
|
|
|
|||
|
H(p) |
|
k |
, |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
k 1 |
|
p pk |
|
|
|
|
|
где pk — k-й полюс, Ak — константа разложения при k-м полюсе. |
||||||||||
Подставим H(p) |
(10.4) в (10.3): |
|
|
|
|
|
|
|
|
|
|
M 1 |
A |
|
M 1 |
1 |
|
M 1 |
|||
h(t) L 1 |
k |
Ak L 1 |
|
|
Akejpkt |
|||||
|
|
|||||||||
|
k 1 |
p pk |
|
k 1 |
p pk |
k 1 |
||||
(10.3)
(10.4)
;
определим ИХ БИХ-фильтра из условия инвариантности (10.1):
M 1 |
|
|
|
h(nT) AkejpknT ; |
|
(10.5) |
|
k 1 |
|
|
|
запишем передаточную функцию БИХ-фильтра (10.2): |
|||
|
M 1 |
|
|
H(z) AkejpknT z n . |
|||
n 0 |
k 1 |
|
|
Изменив порядок суммирования: |
|
|
|
M 1 |
|
|
n |
|
. |
||
H(z) Ak ejpkT z |
1 |
||
k 1 |
n 0 |
|
|
4
получим передаточную функцию БИХ-фильтра H(z) в виде суммы простых дробей:
M 1 |
Ak |
|
|
|
H(z) |
|
, |
(10.6) |
|
|
|
|||
k 1 1 ejpkT z |
1 |
|
||
выраженную через параметры передаточной функции АФП (10.4) pk и Ak .
Таким образом, синтез БИХ-фильтра включает в себя следующие этапы:
задание требований к АЧХ БИХ-фильтра;
на их основе формирование требований к АЧХ АФП:
Они полностью совпадают с требованиями к АЧХ БИХ-фильтра, за исключением того, что правая граница основной полосы для БИХ-фильтра fд 
2 для АФП будет равна бесконечности.
синтез АФП — расчет передаточной функции H(p) (10.4);
определение передаточной функции БИХ-фильтра H(z) (10.6).
Как видим, метод чрезвычайно прост, однако необходимо проанализировать АЧХ синтезированного БИХ-фильтра.
В данном методе используется стандартное Z-преобразование.
Ось частот j p-плоскости отображается на z-плоскость в единичную окружность с бесконечным числом оборотов; один оборот окружности соответствует отрезку длиной д 2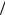 
T (см. Лекцию 3).
Следовательно, ЧХ БИХ-фильтра представляет собой периодическое повторение ЧХ, АФП с периодом д .
Графики АЧХ ФНЧ АФП и БИХ-фильтра
Выводы:
1.На границе основной полосы пропускания д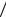 
2 наблюдается эффект наложения АЧХ, называемый элайсингом.
Для его уменьшения можно увеличить частоту дискретизации (но, как правило, она задана) или увеличить порядок БИХ-фильтра.
Поэтому данный метод не позволяет синтезировать оптимальный БИХ-фильтр.
Оптимальным называют БИХ-фильтр минимального возможного порядка при заданных требованиях к АЧХ.
2. Метод не рекомендуется использовать для синтеза ФВЧ и РФ.
10.3.Метод билинейного Z-преобразования
Встандартном Z-преобразовании переменные z и p связаны соотношением (Лекция 3):
z epT , |
откуда p |
1 |
lnz. |
|
T
5
Разложим функцию lnz в ряд Тейлора: |
|
|
|
|
|
|
|
|
|
|||
z 1 |
|
|
1 |
z 1 3 |
|
|||||||
lnz 2 |
|
|
|
|
|
|
|
|
|
|
... . |
|
|
|
3 |
|
|
||||||||
z 1 |
|
|
z 1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Взяв один член ряда, получим формулу билинейного Z-преобразования: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
p |
1 z |
1 |
, |
(10.7) |
||||||
|
|
1 z |
1 |
|||||||||
|
|
|
|
|
|
|
|
|
||||
и наоборот: |
|
|
|
|
|
|
|
|
|
|||
|
|
z |
p |
, |
|
(10.8) |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
p |
|
|
|
|||
где 2 .
T
В этом случае передаточная функция БИХ-фильтра будет связана с передаточной функцией АФП соотношением:
H(z) H(p)
p 1 z 1
1 z 1
10.4. Свойства билинейного Z-преобразования
Ранее было рассмотрено отображение p-плоскости на z-плоскость для стандартного Z-преобразования, в частности:
ось частот j p-плоскости на z-плоскости отображалась в единичную окружность с бесконечным числом оборотов;
левая p-полуплоскость на z-плоскости отображалась в единичный круг.
нормированная частота АФП связана с частотой ЦФ линейно:
T .
Сравним свойства билинейного Z-преобразовании со свойствами стандартного Z- преобразования.
Во избежание путаницы обозначим ось частот АФП на p-плоскости как j . 1. Ось частот p-плоскости p j .
По формуле (10.8):
|
p |
|
|
j |
|
|
|
|
|
|
|||
z |
|
rej |
rej , |
||||||||||
|
|
|
|||||||||||
|
p |
|
j |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
r |
|
|
2 |
2 |
|
1; |
|
|||||
|
|
|
2 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2arctg |
|
|
||||||||
|
|
|
|
|
|
|
(10.9) |
||||||
|
|
|
|
|
|
||||||||
0 0
Выводы:
Ось частот j отображается в единичную окружность (один оборот).
Это означает, что бесконечная ось j сжимается в конечный отрезок длиной
2 , что в шкале частот соответствует д .
6
Следовательно, ЧХ БИХ-фильтра представляет собой периодическое повторение сжатой конечной ЧХ АФП с периодом д .
При этом элайсинг отсутствует.
Графики АЧХ ФНЧ АФП и БИХ-фильтра
2. Левая p-полуплоскость: p j , 0:
z j rej ,j
r |
( )2 2 |
1; |
|||||
( )2 2 |
|||||||
|
|
|
|
||||
|
|
|
|
||||
arctg |
|
arctg |
|
. |
|||
|
|
||||||
|
|
|
|
|
|||
Вывод: левая p-полуплоскость отображается в единичный круг.
3.Соотношение между частотами АФП и БИХ-фильтра — нелинейное (см. (10.9):
tg . |
|
(10.10) |
2 |
|
|
|
|
|
0 |
π |
ω |
Рис. 10.3. Соотношение между частотами АФП и ЦФ
Таким образом, «платой» за отсутствие элайсинга является необходимость пересчета граничных частот АФП, и, кроме того, несовпадение ИХ и ФЧХ БИХ-фильтра и АФП, но последнее и не входило в задачу.
10.5. Процедура синтеза БИХ-фильтра методом билинейного Z- преобразования
1.Задание требований к АЧХ БИХ-фильтра.
2.Формирование требований к АЧХ АФП.
Граничные частоты — пересчитываются по формуле (10.10).
Максимально допустимые отклонения — не меняются.
7
3.Выбор типа АФП (и БИХ-фильтра) (см.разд. 10.1).
4.Синтез АФП — расчет H(p) АФП.
В этом методе H(p) представляется в |
виде произведения |
простейших |
|
множителей, поэтому рассчитываются ее нули |
p k и полюсы p k . |
|
|
5. Синтез ЦФ — расчет H(z). |
|
|
|
Для представления H(z) |
в виде произведения простейших |
множителей |
|
рассчитываются ее нули z k |
и полюсы z k по формуле (10.8). |
|
|
6.Выбор структуры БИХ-фильтра — каскадной из биквадратных звеньев.