Добавил:

naklpakl Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Цифровая обработка сигналов

Файл:

лекции / DSP_11

.pdf

Скачиваний:

Добавлен:

28.04.2023

Размер:

215.25 Кб

Скачать

☆

Лекция 11. Дискретные сигналы

1.Описание дискретных сигналов в частотной области.

2.Основные свойства спектральной плотности.

3.Связь спектральных плотностей дискретного и аналогового сигналов.

4.Операции со спектральной плотностью (сдвиг, инверсия, формирование сигнала с ОБП)

11.1.Описание дискретных сигналов в частотной области

Вz-области дискретный сигнал описывается своим z-изображением:


	X(z) x(nT)z n	.	(11.1)
	n 0
Выполнив в (11.1) замену z ej T , переходим от			Z-преобразования к
преобразованию Фурье дискретного сигнала:

X(ej T ) x(nT)e j Tn ,			(11.2)

n 0

результат которого — Фурье-изображение — называют спектральной плотностью

(СП) дискретного сигнала.

В шкале дискретного нормированного времени и нормированной частоты:


X(ej )	x(n)e j n .		(11.3)

n 0

СП связана с z-изображением соотношением:


X(ej ) X(z)	z ej .	(11.4)

11.2.Основные свойства спектральной плотности:

1.СП дискретного сигнала — непрерывная функция частоты.

2.СП дискретного сигнала — периодическая функция частоты, т. к. периодичен ее

аргумент ej .

Период равен:

fд

2π f ωд T .

Вывод: в частотной области переход к дискретному сигналу — t nT —

сопровождается периодичностью СП.

3.Свойство линейности СП: спектральная плотность линейной комбинации дискретных сигналов равна линейной комбинации СП данных сигналов:

x(n) a1x1(n) a2x2(n) ...

				X
X(ej ) a X	1	(ej ) a	2	X	2	(ej ) ...
1	1		2		2

Доказательство следует из определения СП (11.3).

4.Для вещественного дискретного сигнала модуль СП — четная, а аргумент — нечетная функция частоты.

Доказательство аналогично доказательству для АЧХ и ФЧХ (см. разд. 5.4).

Ведь ЧХ — это Фурье-изображение ИХ, а следовательно, это СП ИХ.

СП комплексного дискретного сигнала не обладает этим свойством.

Поэтому модуль и аргумент СП вещественного дискретного сигнала рассматривают в основной полосе частот [0; ], а комплексного — на периоде [ ; ].

5.Равенство Парсеваля (без доказательства):


		2	T	T	X(ej T )	2 d .
	x(nT)		T				(11.5)
	x(nT)		2				(11.5)
n 0			2

Слева имеем энергию дискретного сигнала согласно ее определению.

Отметим, что понятие «энергии» для дискретного сигнала (последовательности чисел) введено условно (у чисел энергии нет), по аналогии с энергией аналогового сигнала (площадью).

Справа — та же энергия, вычисленная в частотной области — по модулю СП на периоде.

Равенство Парсеваля — это равенство между значениями энергии, вычисленными во временной и частотной областях.

6. Сдвиг СП вправо		на частоту									дискретного
6. Сдвиг СП вправо		на частоту			0 — соответствует умножению						дискретного

сигнала на экспоненту ej 0n :

				x(n) X(ej ) ;


			x(n)ej 0n X ej( 0)					.			(11.6)
				Доказательство:
					по формуле (11.3):
Определим СП сигнала x(n)ej 0n					по формуле (11.3):

	x(n)ej 0n e j n				x(n)e jn( 0 )		X ej( 0)			.
	n 0				n 0
Сдвиг СП влево на частоту
Сдвиг СП влево на частоту			0 — соответствует умножению дискретного сигнала

на экспоненту e j 0n :

				x(n)e j 0n		X ej( 0)			.		(11.7)

Вывод: Если x(n) — вещественный сигнал, то модуль его СП симметричен

относительно оси ординат (четная функция). При умножении на экспоненту сигнал становится комплексным, а модуль его СП — несимметричным относительно оси ординат.

7.Сдвиг (задержка) дискретного сигнала:

Дискретному сигналу, задержанному на m отчетов, соответствует умножение СП

на экспоненту e j m :


x(n) X(ej )

	.	(11.8)
x(n m) X(ej )e j m	.	(11.8)

Доказательство:

В z-области, согласно теореме о задержке, имеем Z-изображение: x(n m) X(z)z m,

что соответствует (11.8) при подстановке z ej .

11.3. Связь спектральных плотностей дискретного и аналогового сигналов

Если дискретный сигнал x(nT) получен в результате дискретизации аналогового сигнала x(t), то связь между их СП имеет вид (без доказательства):

1					2
X(ej T )		X	а j	m		.	(11.9)
					T
	T m

Спектральная плотность дискретного сигнала равна (с точностью до множителя

1 ) бесконечной сумме копий СП аналогового сигнала, сдвинутых друг

относительно друга по оси частот на частоту дискретизации д 2 .

Связь (11.9) иллюстрирует рис. 11.1.

Выводы:

Если СП аналогового сигнала финитна и ограничена частотой в , то

1.При д 2 в СП аналогового сигнала совпадает с СП дискретного сигнала на периоде в; в д , поэтому точное восстановление аналогового сигнала гарантируется.

2.При д 2 в наблюдается элайсинг, и СП дискретного сигнала необратимо искажается, поэтому точное восстановление аналогового сигнала невозможно.

Если СП аналогового сигнала нефинитна, то вследствие элайсинга точное
восстановление аналогового сигнала невозможно.
				Xа ( jω)
		в	0	в			ω	а
		в	0	в
				X(ej T )
			0					б
2 д	д в		0	в	д		2 д
				X(ej T )
2 д		в	0				ω	в
2 д	д	в	0	в		д	2 д
				X(ej T )
								г
	2		0		д	2	д
	д	д	в	в	д		д

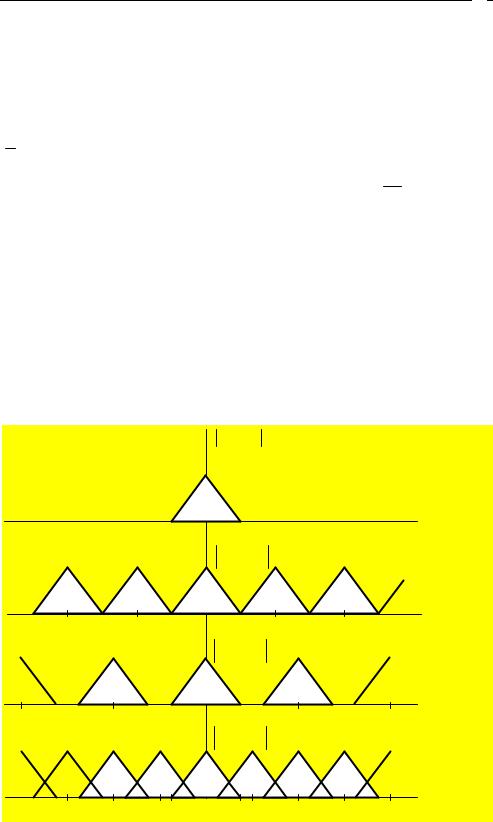
Рис. 11.1. Связь СП дискретного и аналоговых сигналов: модуль финитной СП (а); модуль СП дискретного сигнала при: д 2 в (б); д 2 в (в); д 2 в (г)

11.4.Операции со спектральной плотностью

1.Сдвиг СП — рассмотрен в разд. 11.2.

2.Инверсия СП вещественного сигнала.

Инверсия СП (рис. 11.2) означает, что любая спектральная составляющая 0 модуля СП оказывается на противоположной частоте:

0 0 .

т. е. для модуля СП необходимо выполнить преобразование (рис. 11.2):

			.	(11.10)
X(ej )		X(ej( ))

X(ejω )

			ω

π			π
π	ω0		π
	X(ej
	X(ej	(π ω))

		ω
π		π
	π ω0

Рис. 11.2. Инверсия СП

Инверсную СП можно получить посредством сдвига исходной СП на вправо:


X(ej( )) x(n)e j( )n
X(ej( )) x(n)e j( )n		x(n)cos( )n j x(n)sin( )n Re jIm
	n 0	n 0	n 0
Инверсная СП:

X(ej( )) X(e j( )) Re jIm

Модули СП совпадают, а аргументы отличаются знаком.

Сдвиг СП вправо реализуется посредством умножения x(n) на ej n :

x(n)ej n x(n)cos n ( 1)n x(n)

Вывод: для формирования инверсной СП необходимо изменить знак у каждого нечетного отсчета дискретного сигнала.

( 1)n

x(nT)						y(nT) ( 1)n x(nT)
x(nT)						y(nT) ( 1)n x(nT)

Рис. 11.3. Алгоритм реализации инверсии СП

3.Формирование сигнала с ОБП.

На рис. 11.4 , а — СП вещественного сигнала с двумя БП. Будем выделять

правую полосу.

Алгоритм формирования сигнала с ОБП включает в себя следующие шаги

(рис. 11.4 и 11.5):

Сдвиг СП влево на частоту — рис. 11.4, б:


	1	2	.	(11.11)
			.	(11.11)
	2
	2
Реализация сдвига влево (рис. 11.5):

y (n) x(n)e j n		Y (ej ) .
1		1

Фильтрация комплексного сигнала y1(n) с помощью комплексного ФНЧ (КФНЧ).

КФНЧ представляет собой два ФНЧ для вещественной и комплексной частей сигнала.

На рис. 11.4, в представлено условное изображение АЧХ КФНЧ.

На рис. 11.4, г — СП Y2(ej ) на выходе КФНЧ.

На рис. 11.5 — комплексный сигнал y2(n) на выходе КФНЧ.

Сдвиг СП Y2(ej ) частоту вправо (на свое место) — рис. 11.4, д:

y(n) y2(n)ej n

Y(ej ).

X(e jωT )

ωд

ω1 ω2

ωд

Y (e jωT

)

АЧХ

Y (ejωT )

Y(ejωT )

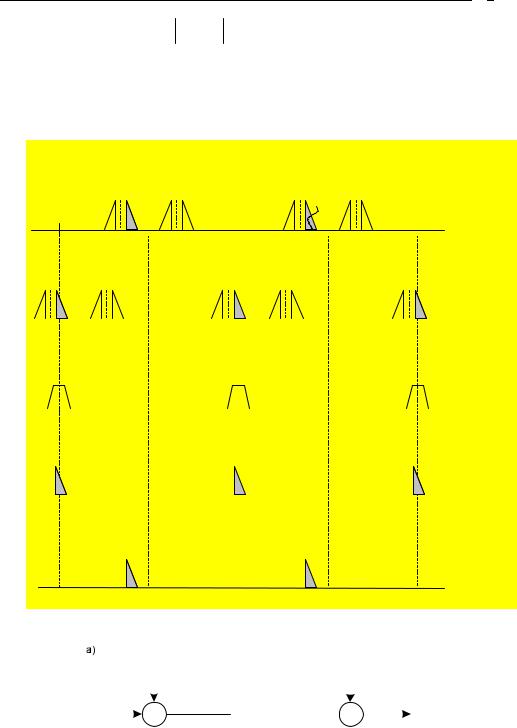
Рис. 11.4. Формирование сигнала с ОБП

e jω nT

ejω nT

x(nT)

y1(nT)

y2(nT)

y(nT)

КФНЧ

Рис. 11.5. Алгоритм формирования сигнала с ОБП

Соседние файлы в папке лекции

#
28.04.2023351.57 Кб10DSP_1.pdf
#
28.04.2023232.75 Кб32DSP_10.pdf
#
28.04.2023215.25 Кб13DSP_11.pdf
#
28.04.2023203.63 Кб19DSP_12.pdf
#
28.04.2023283.88 Кб12DSP_13.pdf
#
28.04.2023242.02 Кб6DSP_14.pdf
#
28.04.2023233.38 Кб6DSP_15.pdf
#
28.04.2023237.41 Кб10DSP_2.pdf