6

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические методы защиты информации

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6

Изучение и исследование блокового шифра AES

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А.

(Ф.И.О) (подпись)

Цель лабораторной работы

Изучить преобразования, выполняемые при шифровании и дешифровании сообщений в блоковом шифре AES, а также исследовать некоторые его свойства.

Ход выполнения работы

Случайный ключ:

Случайный блок данных:

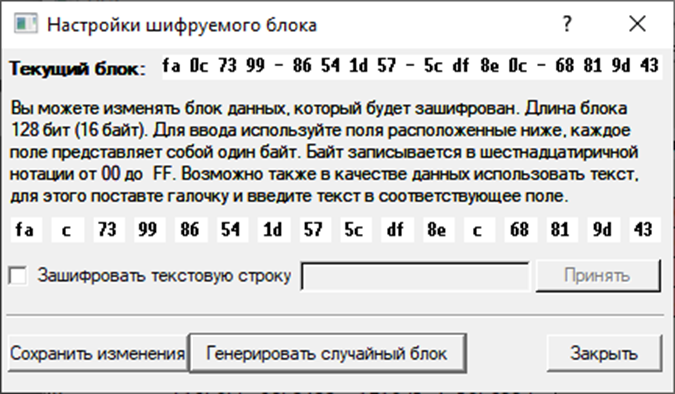
Выполняем процедуру шифрования, наблюдая последовательность выполняемых преобразований на каждом раунде, включая и преобразования раундовых ключей:

0:

1:

2:

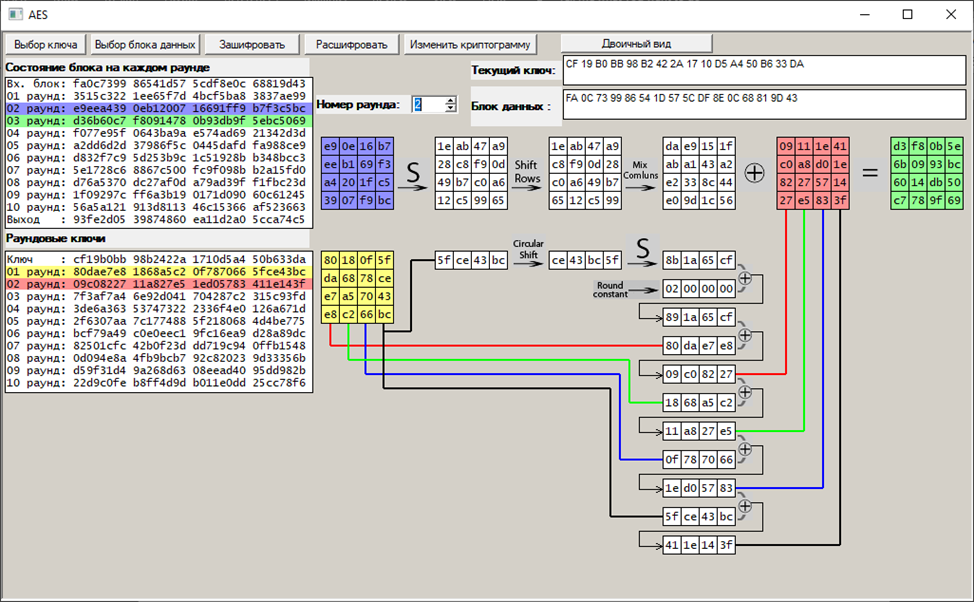
10:

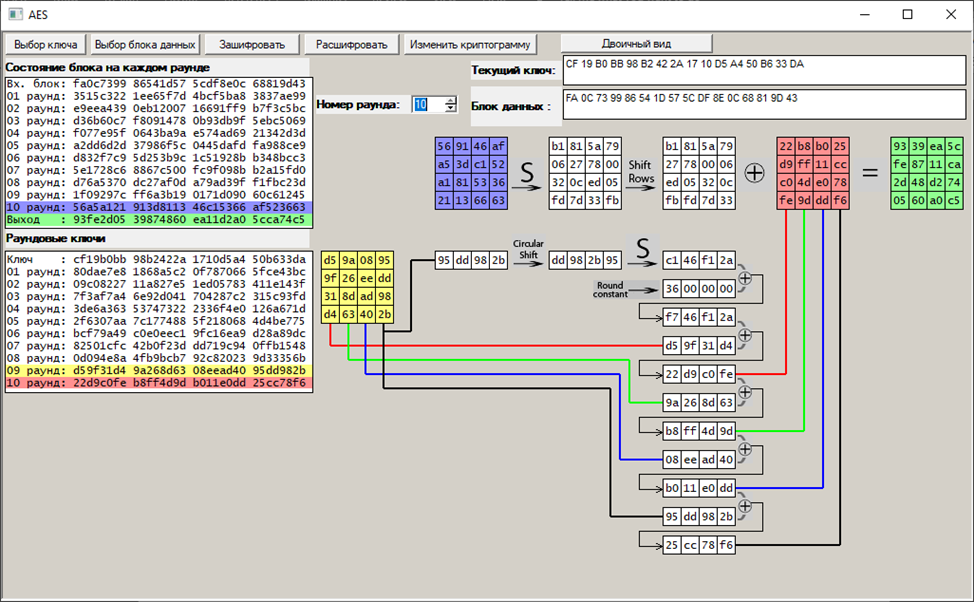
Выполняем процедуру дешифрования, наблюдая последовательные преобразования криптограммы в открытое сообщение, убеждаемся в обратном порядке формирования раундовых ключей:

0:

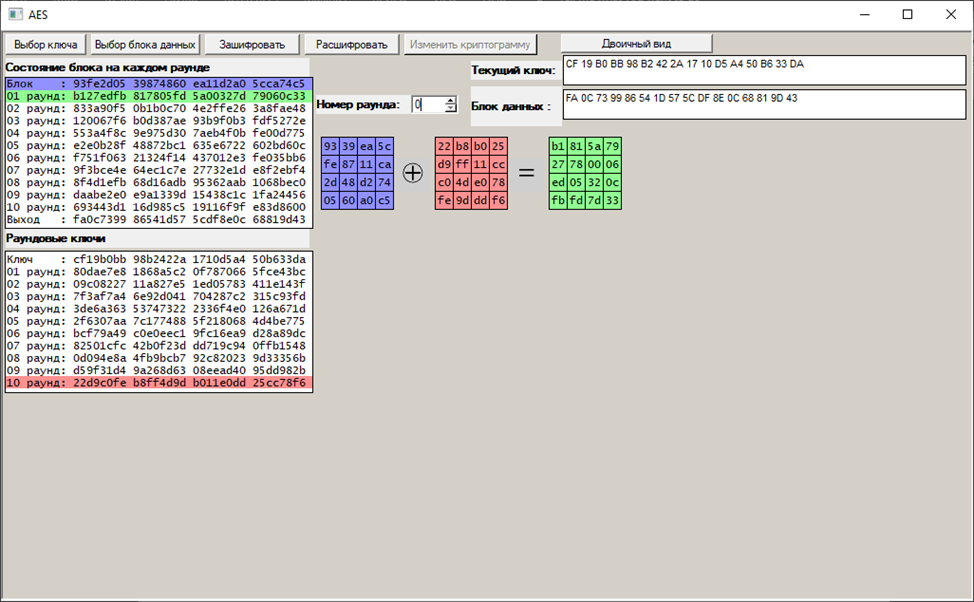
1:

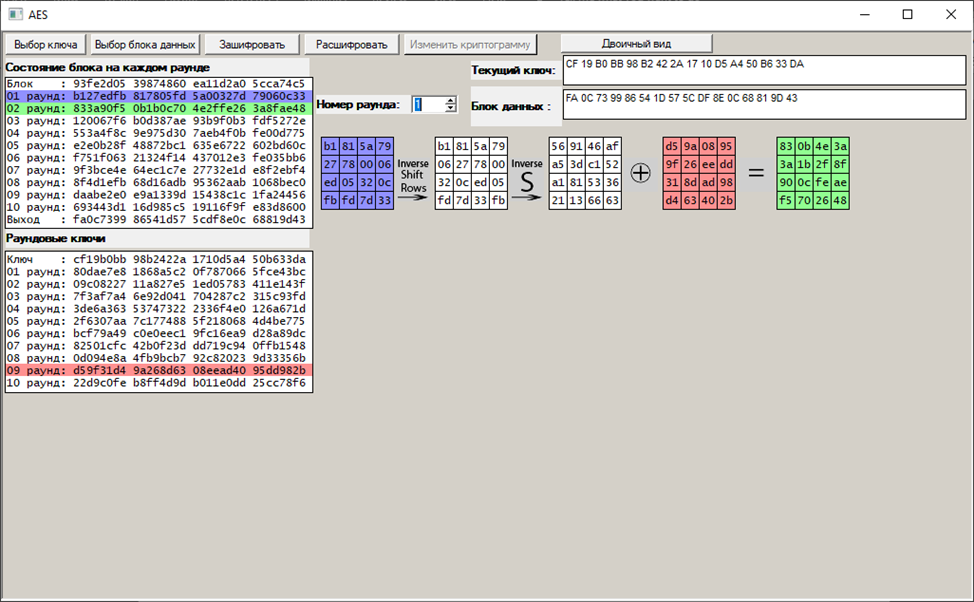
2:

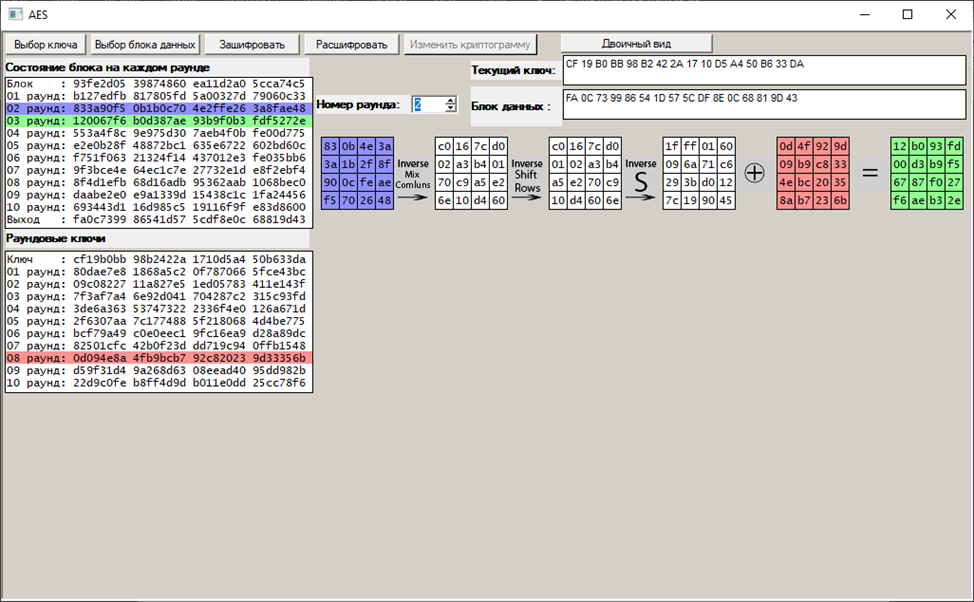
10:

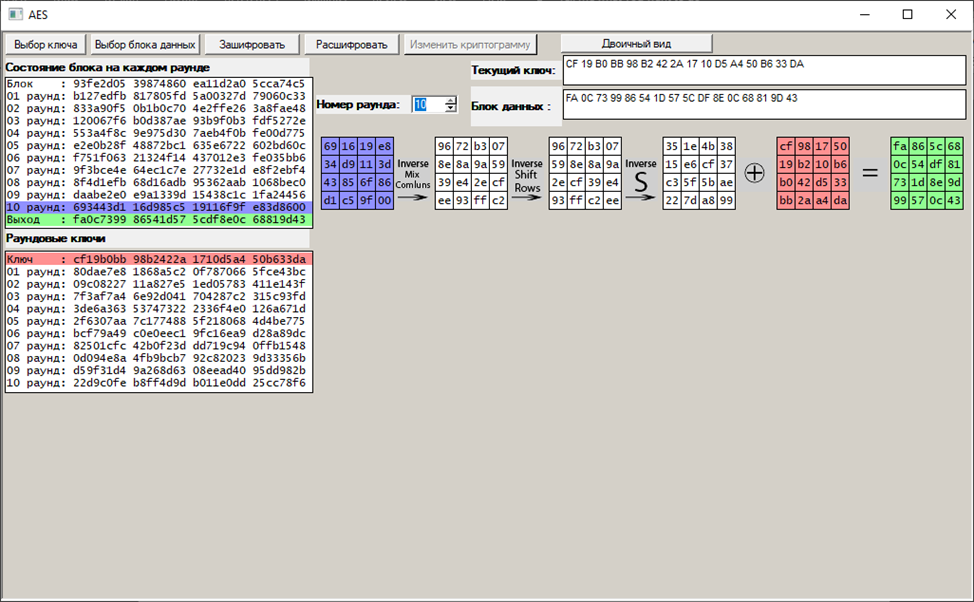
Далее, выберем один из раундов и изучим алгоритм формирования обратных элементов конечного поля и аффинно-линейное преобразование:

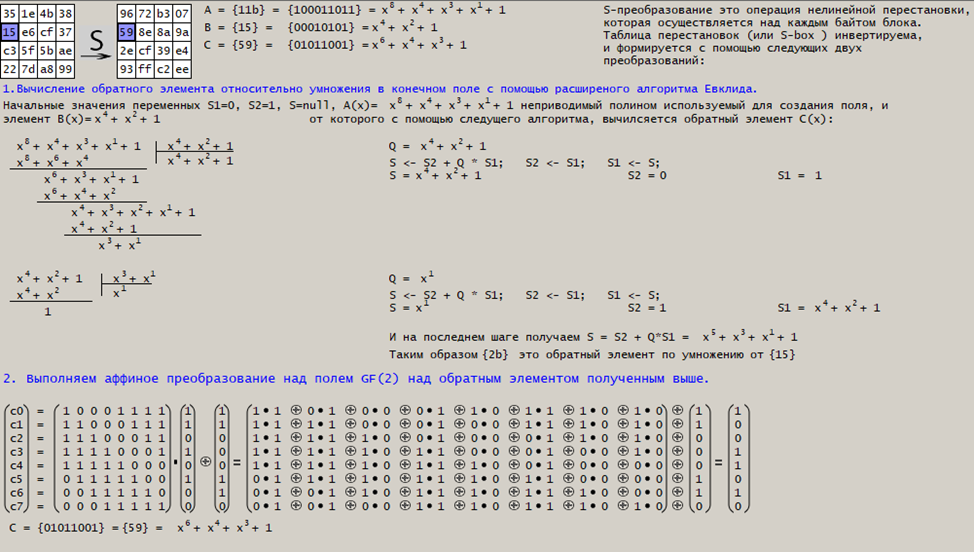
Проверяем при помощи вычислений на бумаге правильность нахождения обратного элемента в конечном поле GF(2⁸) для заданного неприводимого полинома, образующего это поле:

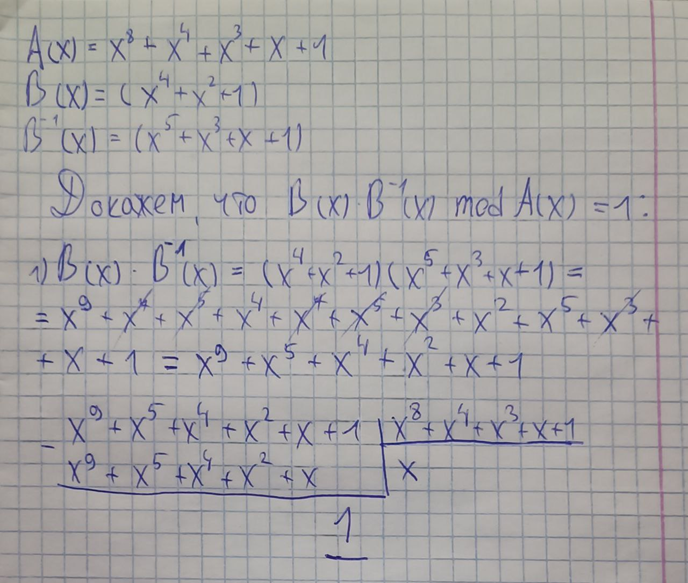
Элемент 2b – это обратный элемент по умножению от 15.

Рассмотрим структуру операции “Mix Columns”:

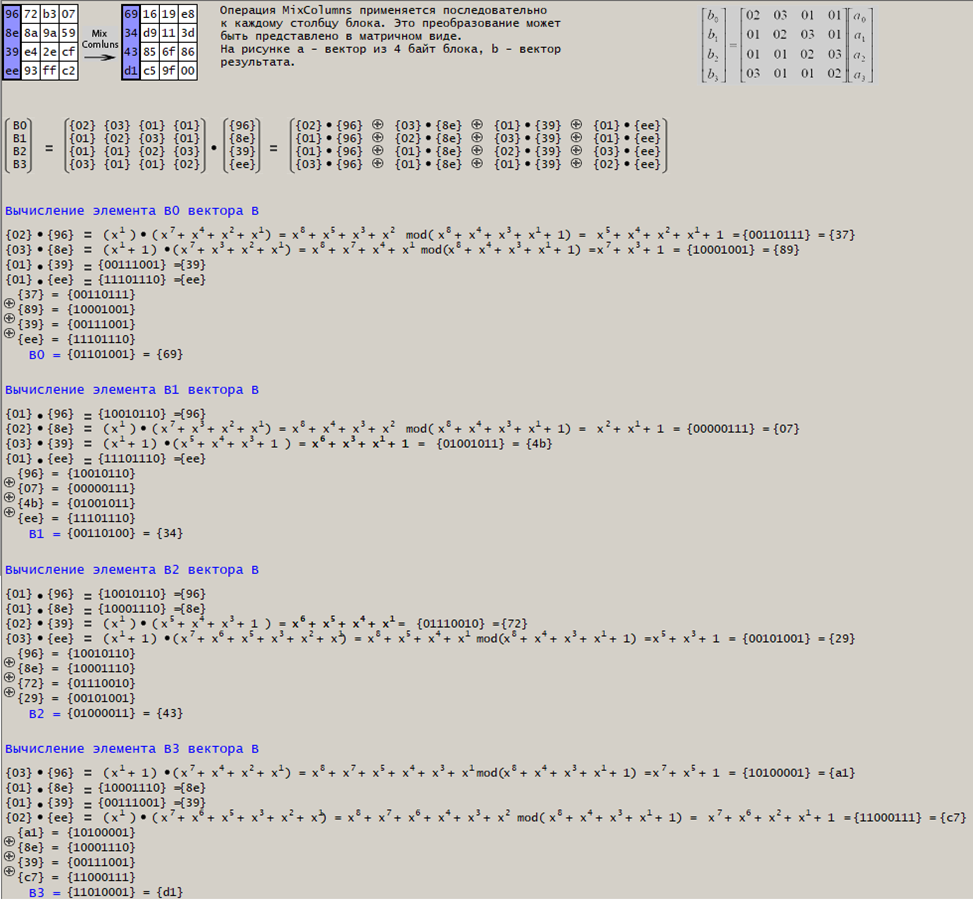
Далее, рассмотрим первые три раунда при следующих данных:

При ключе, состоящим из всех нулей:

Первый раунд:

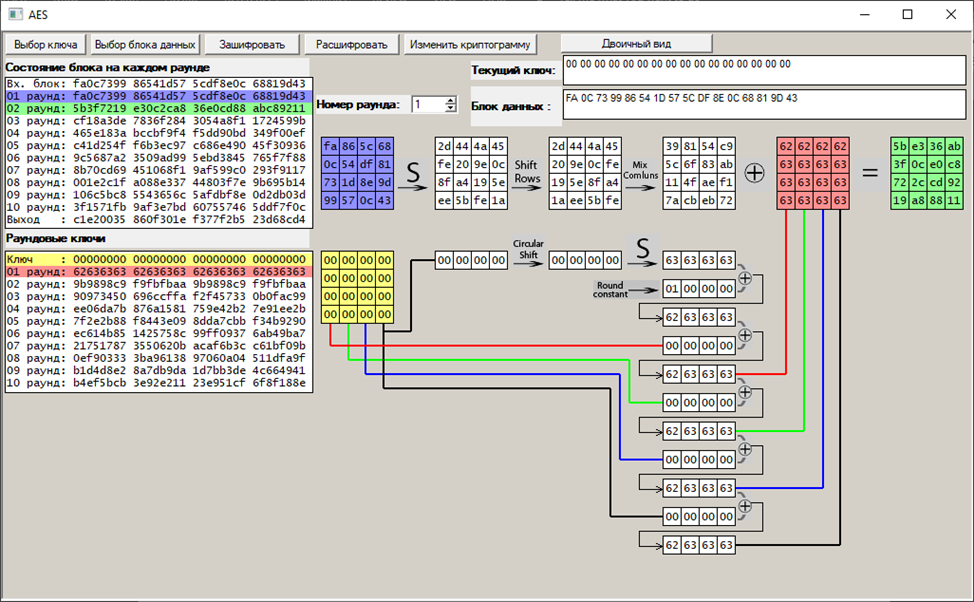
Второй раунд:

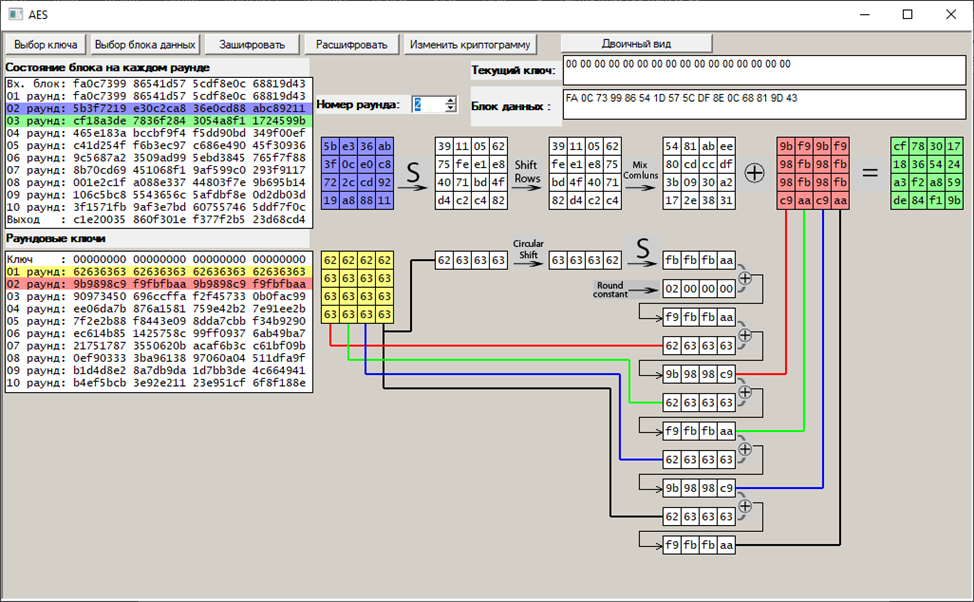
Третий раунд:

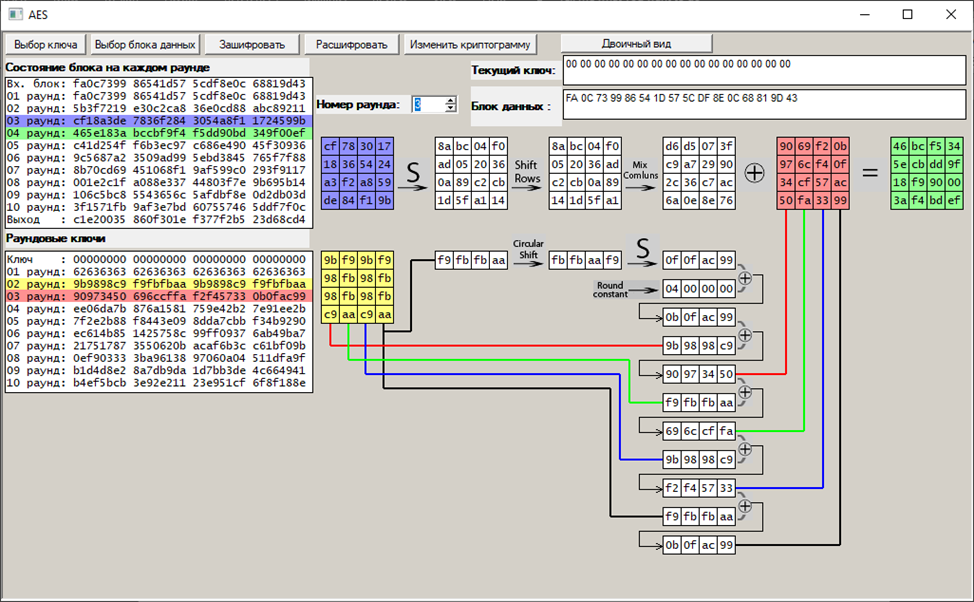
Видим, что при каждом последующем раунде, наблюдается увеличение «случайности» раундовых ключей и промежуточных криптограмм.

При случайном ключе и открытом сообщении, состоящим из всех нулей:

Первый раунд:

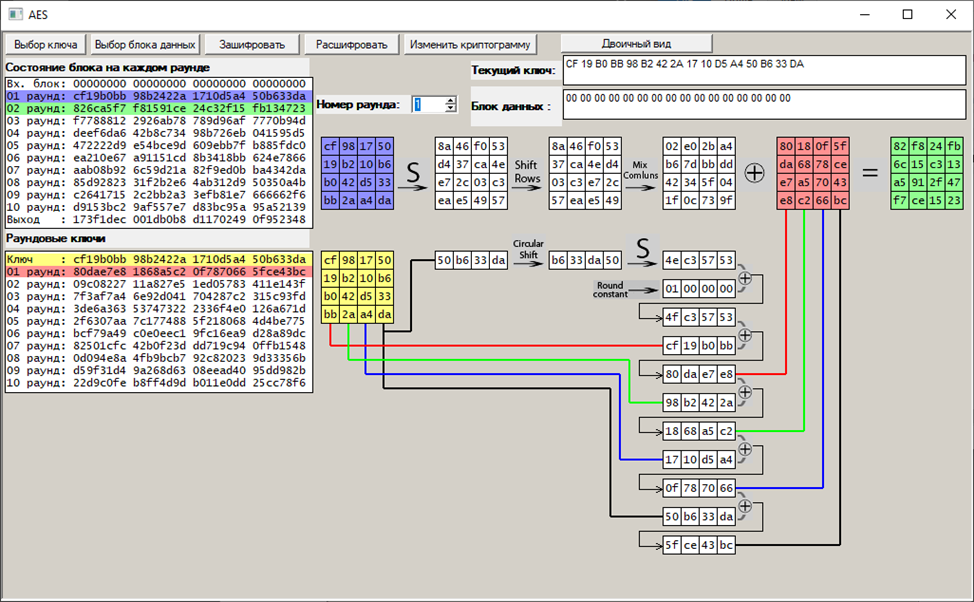
Второй раунд:

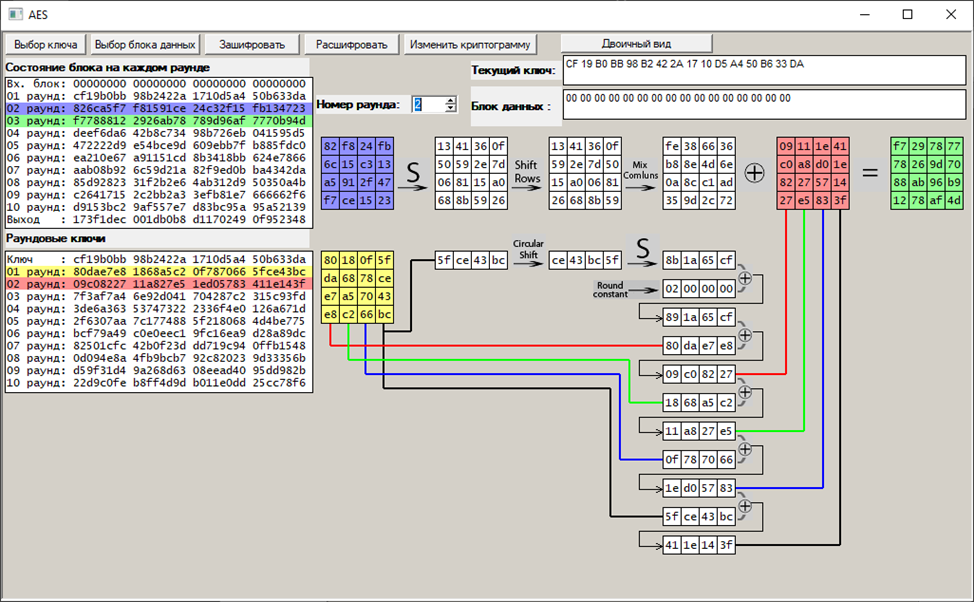
Третий раунд:

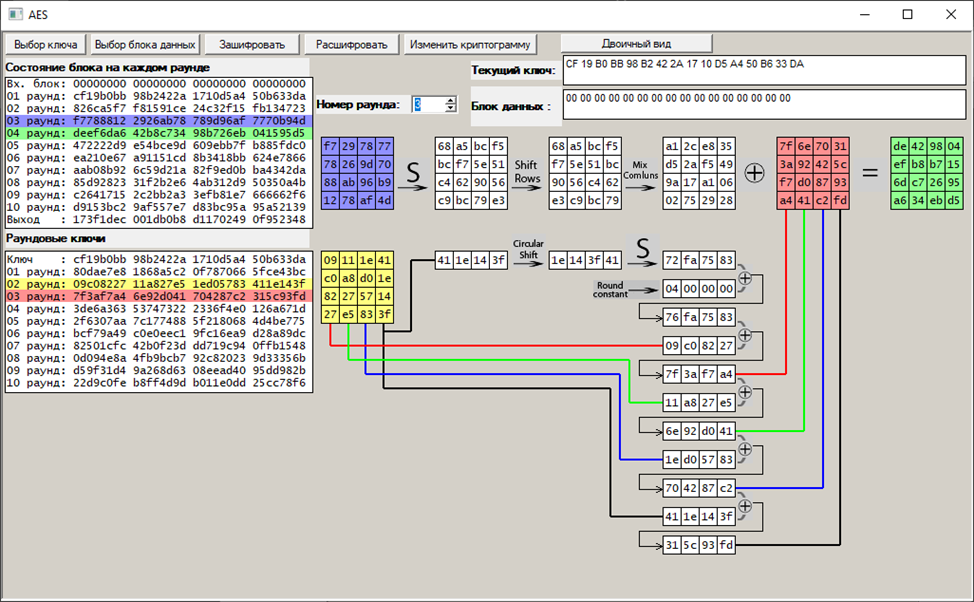
При случайном ключе и открытом сообщении, состоящим из единицы на 108 месте и остальных нулей:

Первый раунд:

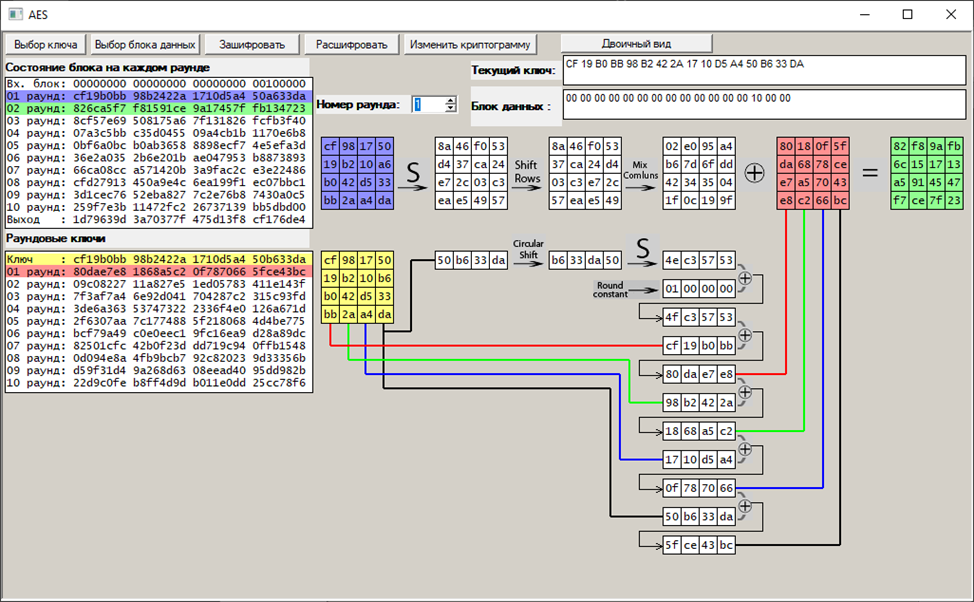
Второй раунд:

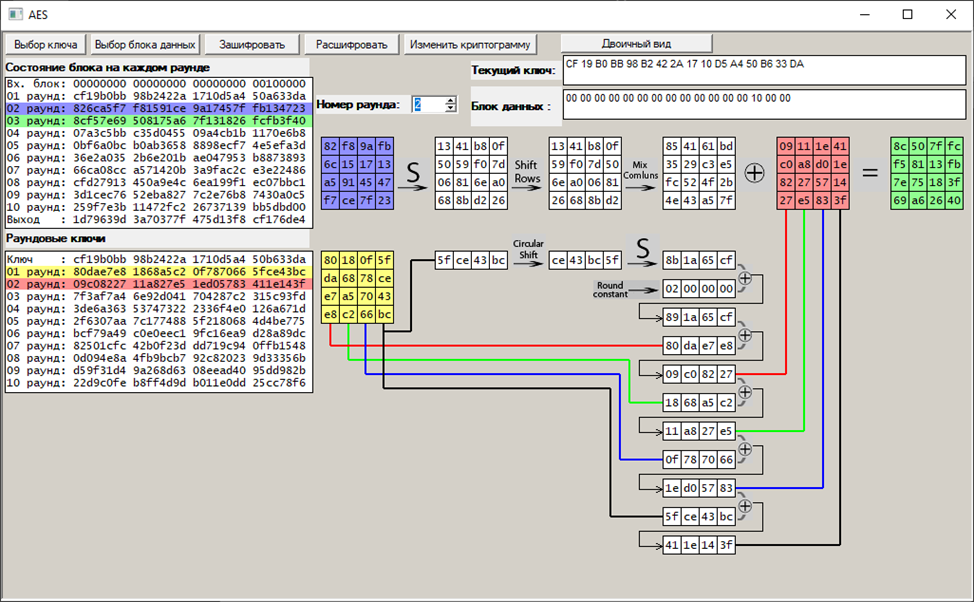
Третий раунд:

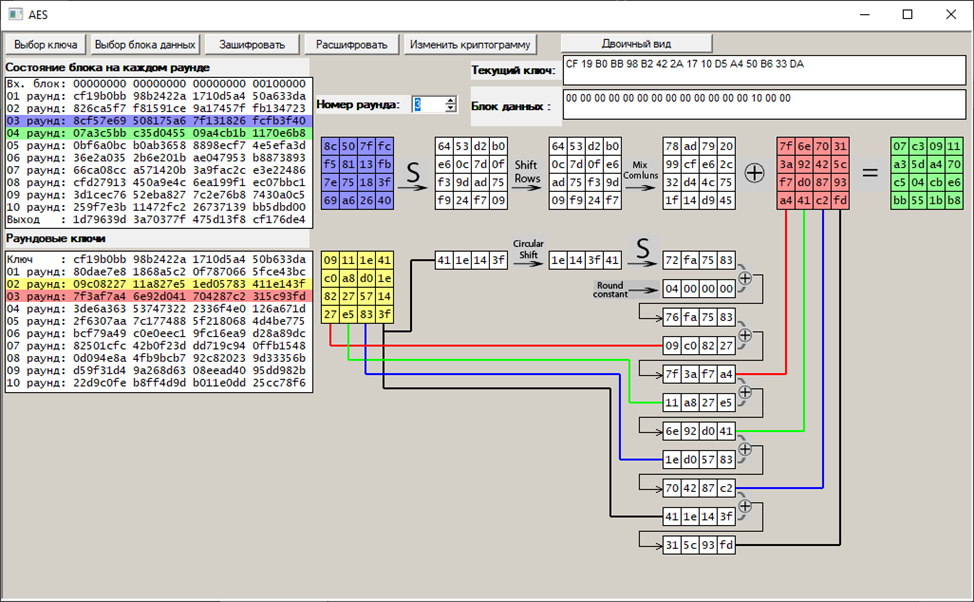
Сравним по раундам промежуточные криптограммы при сообщении из всех нулей и сообщении из одной единицы и остальных нулей. Различающееся количество бит называется коэффициентом лавинного эффекта; найдем его:

Раунд	без/с “1”	Промежуточная криптограмма	Кол-во разных бит	Коэфф-нт лавинного эффекта
1	без “1”	cf19b0bb98b2422a1710d5a450b633da	1	0,8%
	с “1”	cf19b0bb98b2422a1710d5a450a633da
2	без “1”	826ca5f7f81591ce24c32f15fb134723	18	14,1%
	с “1”	826ca5f7f81591ce9a17457ffb134723
3	без “1”	f77888122926ab78789d96af7770b94d	72	56,2%
	с “1”	8cf57e69508175a67f131826fcfb3f40
4	без “1”	deef6da642b8c73498b726eb041595d5	62	48,4%
	с “1”	07a3c5bbc35d045509a4cb1b1170e6b8
5	без “1”	472222d9e54bce9d609ebb7fb885fdc0	64	50,0%
	с “1”	0bf6a0bcb0ab36588898ecf74e5efa3d
6	без “1”	ea210e67a91151cd8b3418bb624e7866	63	49,2%
	с “1”	36e2a0352b6e201bae047953b8873893
7	без “1”	aab08b926c59d21a82f9ed0bba4342da	56	43,8%
	с “1”	66ca08cca571420b3a9fac2ce3e22486
8	без “1”	85d9282331f2b2e64ab312d950350a4b	52	40,6%
	с “1”	cfd27913450a9e4c6ea199f1ec07bbc1
9	без “1”	c26417152c2bb2a33efb81e7666662f6	69	53,9%
	с “1”	3d1cec7652eba8277c2e76b87430a0c5
10	без “1”	d9153bc29af557e7d83bc95a95a52139	67	52,3%
	с “1”	259f7e3b11472fc226737139bb5dbd00

Санкт-Петербург

2022