14

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические методы защиты информации

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №14

Исследование криптосистемы с открытым ключом РША

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А.

(Ф.И.О) (подпись)

Цель лабораторной работы

Закрепить знания, полученные на лекциях, по теме «Криптосистема РША».

Используемое программное обеспечение

Для работы используется программа “RSA”.

Порядок выполнения работы

Выполнение упражнений по возведению в степень больших чисел по модулю

Рассчитаем степени малых чисел по малому модулю и проверим:

Проверка:

e = 31 = 16 +8 + 4 + 2 + 1

2¹ mod 5 = 2

2² mod 5 = 4

2⁴ mod 5 = 1

2⁸ mod 5 = 1

2¹⁶ mod 5 = 1

c = ( (2¹⁶ mod 5) * (2⁸ mod 5) * (2⁴ mod 5) * (2² mod 5) * (2¹ mod 5) ) mod 5 = (1 * 1 * 4 * 2) mod 5 = 3 mod 5 = 3.

Расчет выполнен верно. Далее, рассчитаем степени произвольных больших чисел по модулю прямым методом и быстрым методом:

Прямой метод:

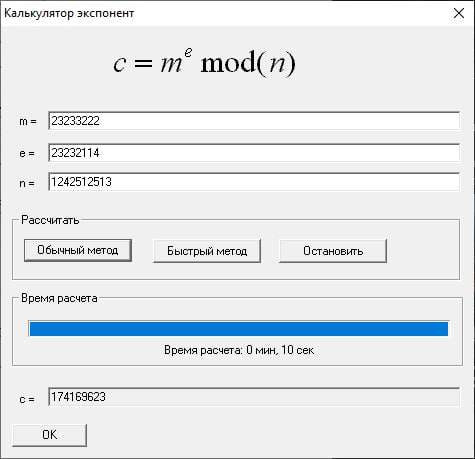
Быстрый метод:

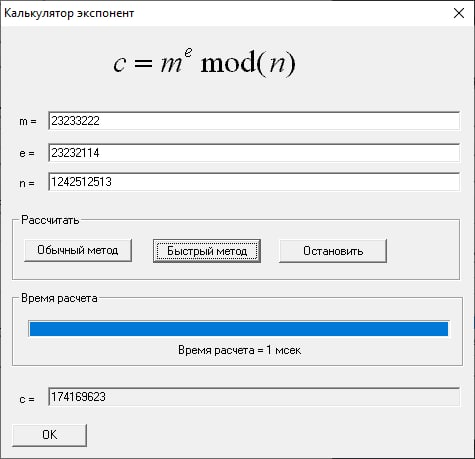
Как видно, быстрый метод гораздо эффективнее прямого.

Генерирование ключей для криптосистемы РША, а также шифрование и дешифрование с ее помощью коротких текстов

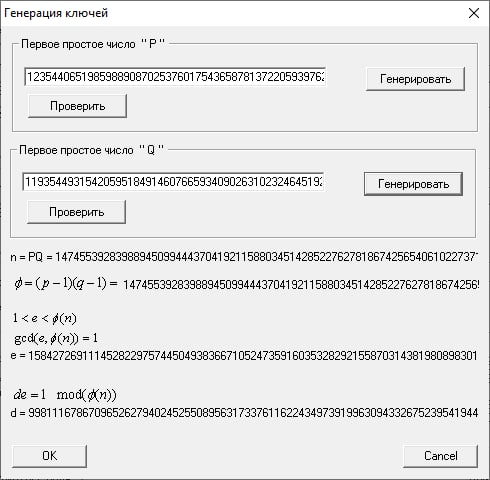
Зададим малые простые числа p, q и сгенерируем ключи для РША.

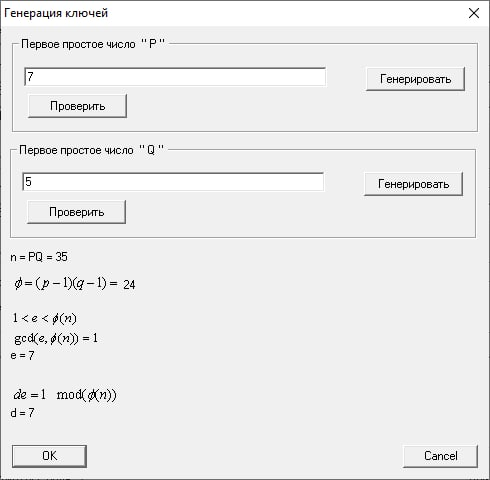
p = 7, q = 5

N = p * q = 7 * 5 = 35

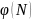= (p – 1) * (q – 1) = 6 * 4 = 24

Открытый ключ e = 7:

НОД(e, = НОД(7, 24) = 1

Закрытый ключ:

d = e^-1 mod = 7

Найдем e^-1:

НОД(e, ) = НОД(7, 24) = 1

24 = 7 * 3 + 3

7 = 3 * 2 + 1

3 = 24 – 7 * 3

1 = 7 – 3 * 2 = 7 – (24 – 7 * 3) * 2 = 7*7 – 2*24

e^-1 = 7

Закрытый ключ d = 7

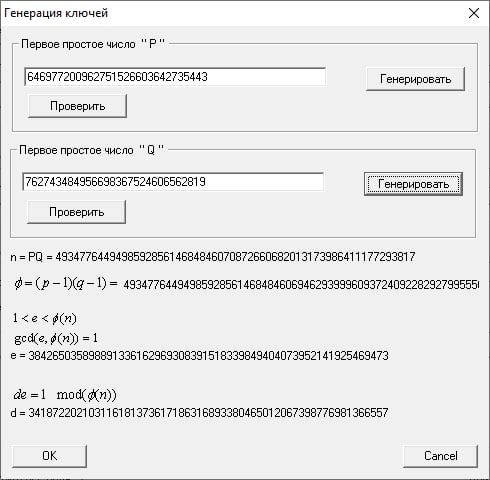
Произведем случайное генерирование простых чисел p, q разрядности по 100 бит каждое, задаваясь количеством проверок n = 20.

Генерация p:

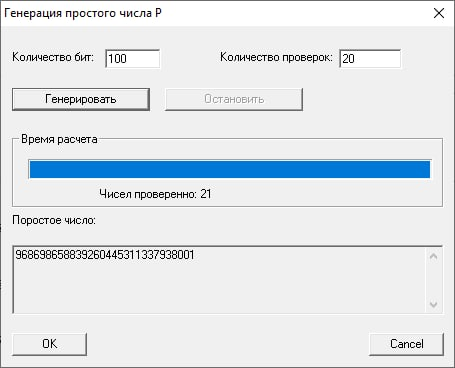
Генерация q:

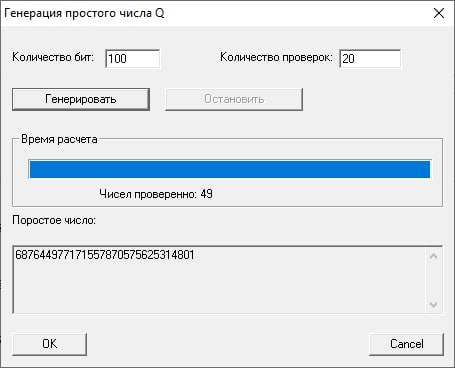
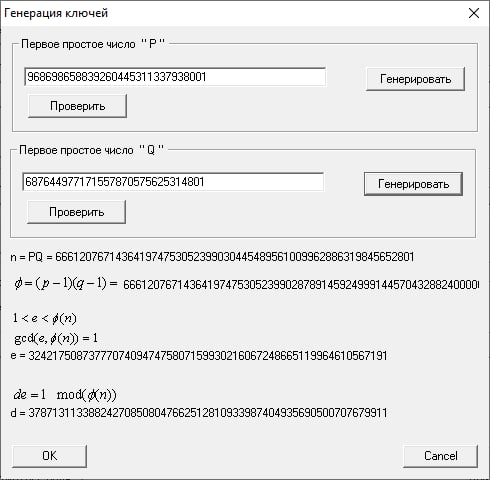
То же самое повторим для n = 30:

Генерация p:

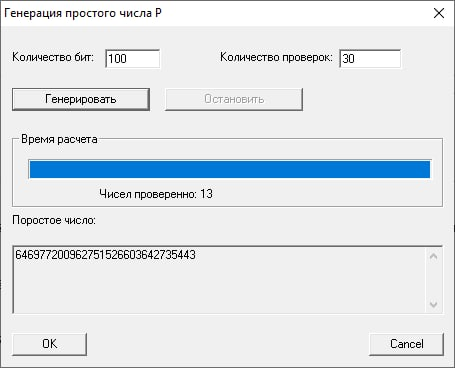
Генерация q:

Вероятность ошибочного тестирования простых чисел при использовании теста ферма

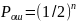
При n = 20:

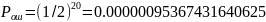
При n = 30:

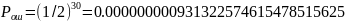
Шифрование файлов большого размера безопасной криптосистемой РША и оценка времени шифрования и дешифрования при ее простейшей программной реализации

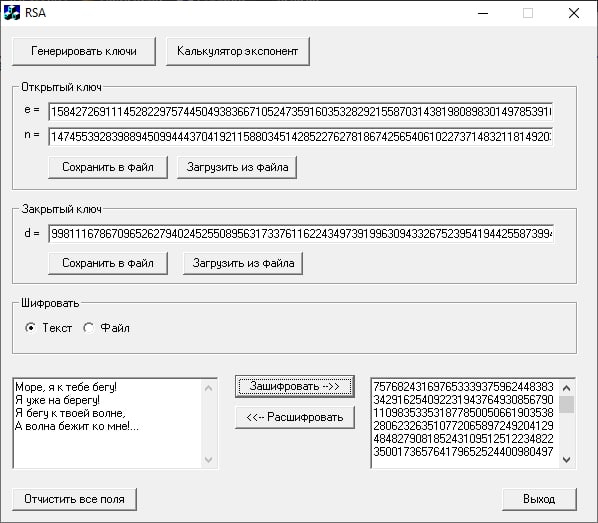
Произведем шифрование короткого смыслового текста, введенного в левое поле:

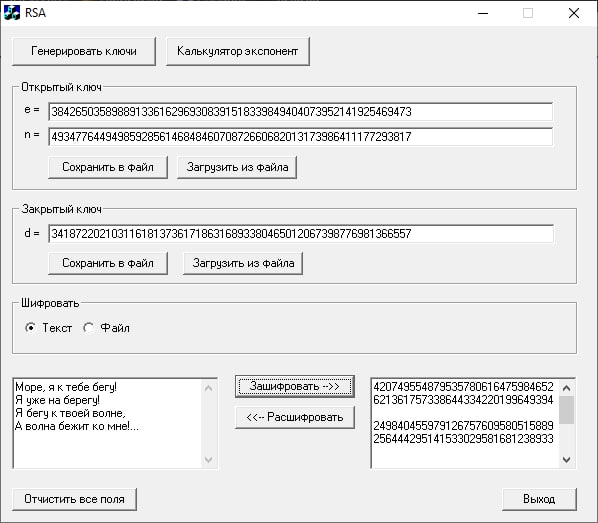
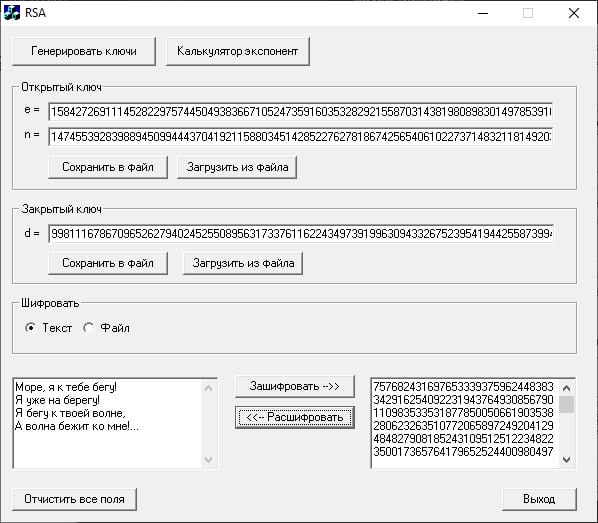
Удалим открытый текст в левом поле и произведем дешифрование криптограммы, содержащейся в правом поле:

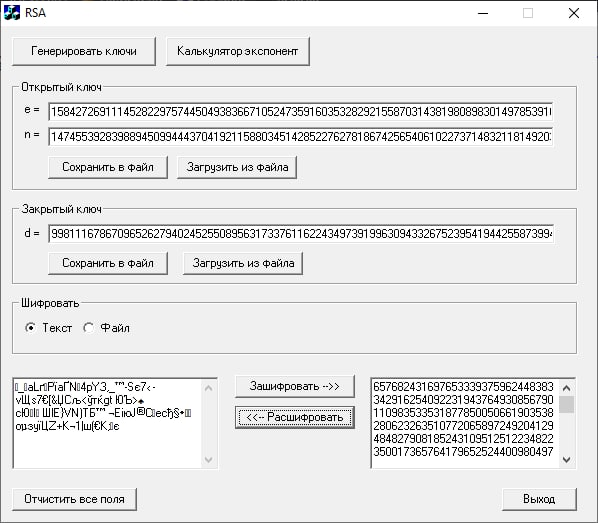
То же самое повторим после изменений одной из цифр криптограммы:

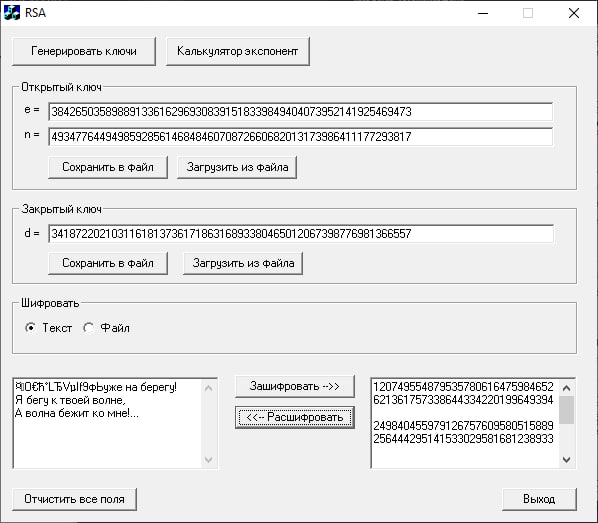
Повторим те же действия, указав разрядность простых чисел p и q по 1024 бита:

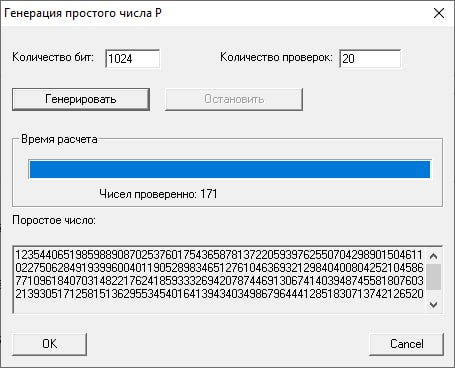
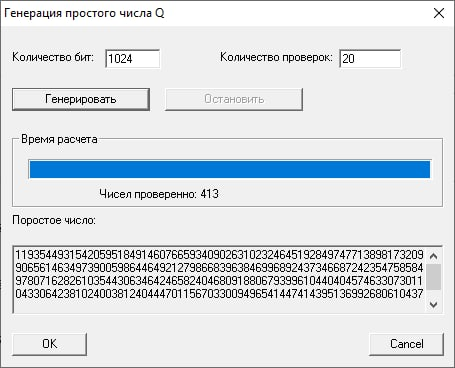
Шифрование:

Дешифрование:

При изменении первой цифры криптограммы:

Произведем шифрование произвольного файла большого объема, фиксируя при этом время шифрования:

Исходное сообщение:

Шифрование файла:

Криптограмма:

Произведем дешифрование криптограммы, помещенной в специальных файл, фиксируя при этом время дешифрования.

Дешифрованная криптограмма:

Рассчитаем скорость шифрования и дешифрования при данной простейшей программной реализации безопасной криптосистемы РША.

Шифрование:

1260624 бит / 86 сек = 14658 бит/сек = 14.31 Кбит/сек

Дешифрование:

1280560 бит / 85 сек = 15065 бит/сек = 14.71 Кбит/сек

Подписание сообщений и проверка подписи

Сгенерируем простые числа с разрядностью 16 бит:

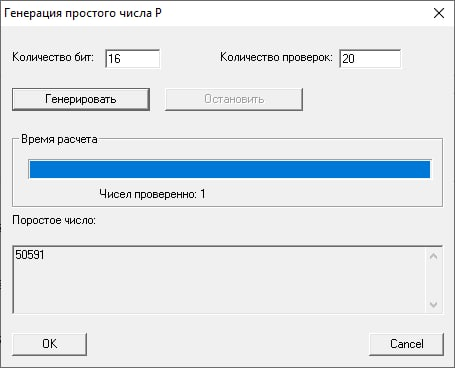
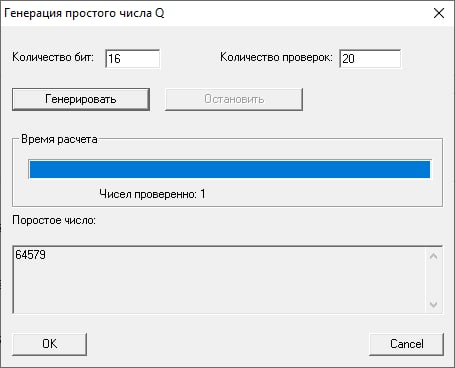
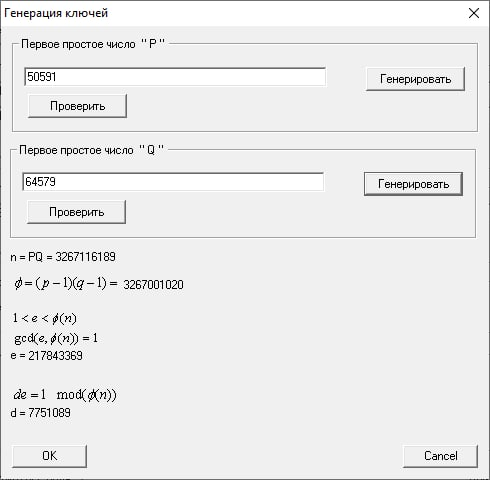
Используя подпрограмму «Калькулятор экспонент» сгенерируем цифровую подпись открытого текста m в виде 9527. Без использования хэш-функции (аналогично шифрованию, но с закрытым ключом) s = m^d mod n. Подписью будет пара чисел (m, s).

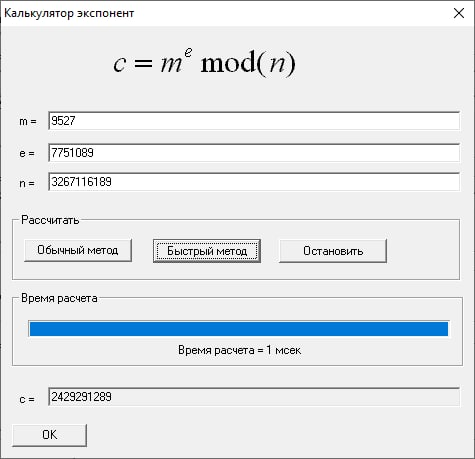
Подпись (9527, 2429291289)

Создадим подделку цифровой подписи путем возведения m и s в степень с произвольным показателем l: m’ = m^l mod n, s’ = s^l mod n.

Пусть l = 3

m’ = m^l mod n = 2187372287:

s’ = s^l mod n = 1697471162:

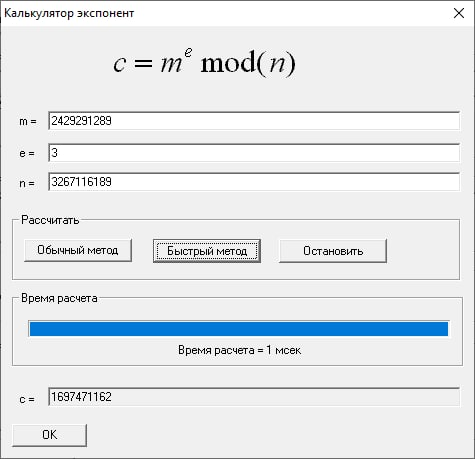
Поддельная подпись (2187372287, 1697471162)

Произведем верификацию цифровой подписи в обоих случаях:

Найдем m₁ = s^e (mod n), и проверим равенство m₁ = m

Равенство выполнилось.

Найдем m₂ = s’^e (mod n) и проверим равенство m₂ = m’.

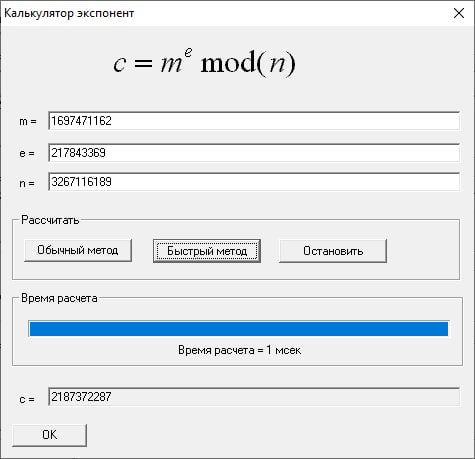
Вычисленное при верификации значение m₂ совпало с ложным открытым сообщением m’, а это значит, что поддельная подпись не выявилась.

Получим хэш-образ открытого текста h(m), используя следующий упрощенный алгоритм: сложить номера всех символов сообщения 9+5+2+7 = 23. Результат умножим на d по mod n:

(23 * 7751089) mod 3267116189 = 178275047‬‬‬

Получим подпись для хэш-образа s = h^d(m) mod n:

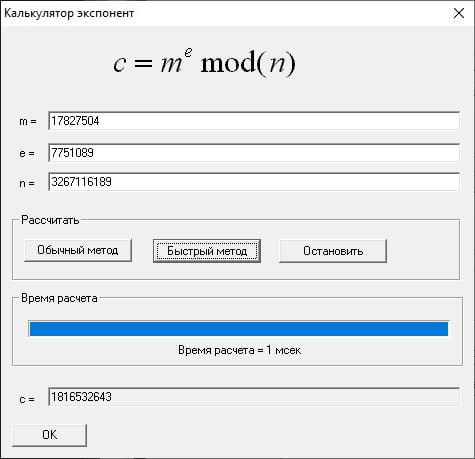
Подпись (m, s) = (9527, 1816532643)

Верифицируем h(m) = s^e mod n:

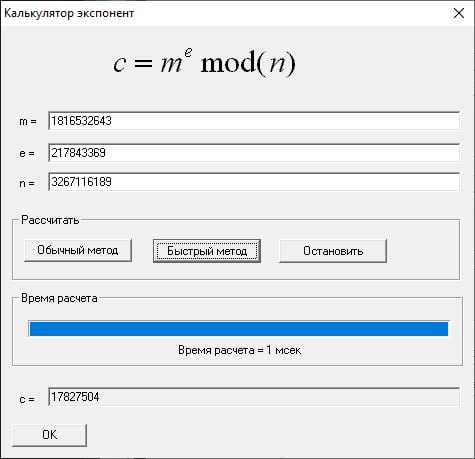
Создадим подделку цифровой подписи путем возведения m и s в степень с произвольным показателем l: m’ = m^l mod n, s’ = s^l mod n:

При l = 8:

m’ = m^l mod n:

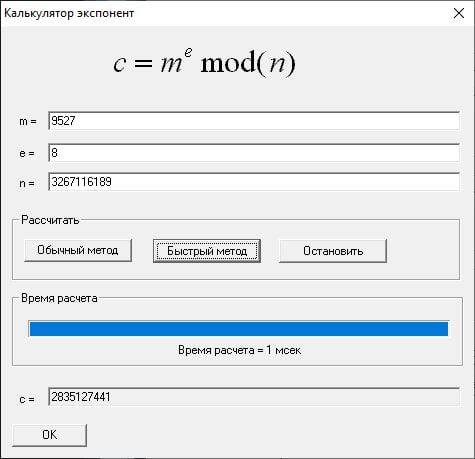
s’ = s^l mod n:

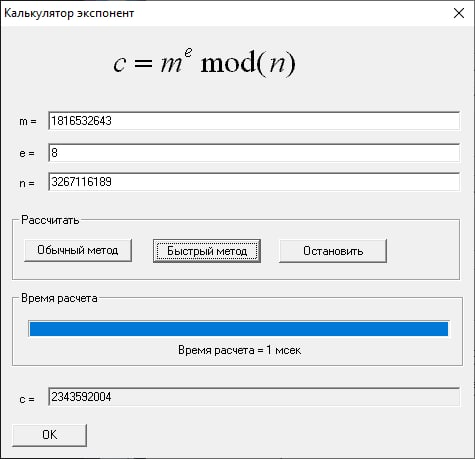
Поддельная подпись (2835127441, 2343592004)

Верифицируем подделанную подпись путем проверки сравнения h(m’) = s^’e (mod n):

s^’e (mod n) = 2343592004^217843369 mod 3267116189 = 621856656.

h(m’):

6+2+1+8+5+6+6+5+6 = 45

(45 * 7751089) mod 3267116189 = 348799005

Как видно, равенство не выполняется, следовательно, верификация не прошла.

Применение хэш-функции усиливает безопасность подписи и целостность открытого текста.

Обмен зашифрованными и подписанными сообщениями в локальной сети

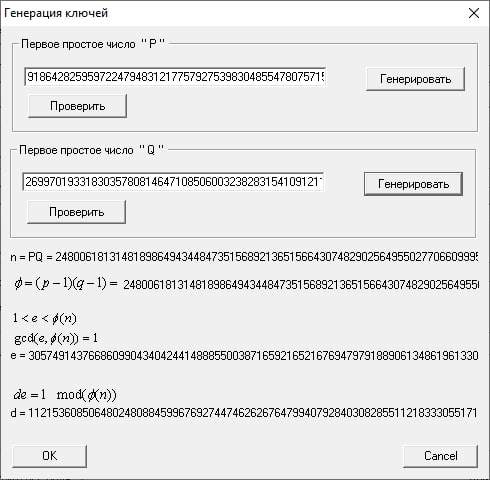
Проведем генерацию ключей. Открытый ключ (N, e) сохраним как файл в общедоступной папке. Имя файла – Ключ Яковлев.

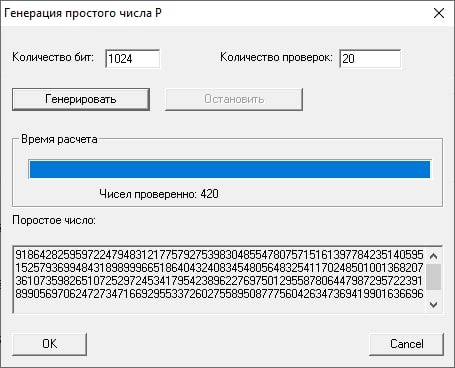
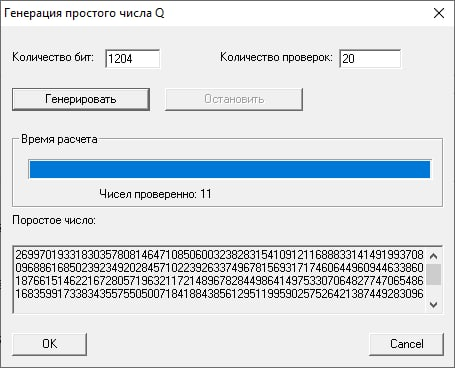
Подготовим два коротких текстовых сообщения в программе Блокнот (Сообщение1 Яковлев, Сообщение2 Яковлев).

Сообщение 1:

Сообщение 2:

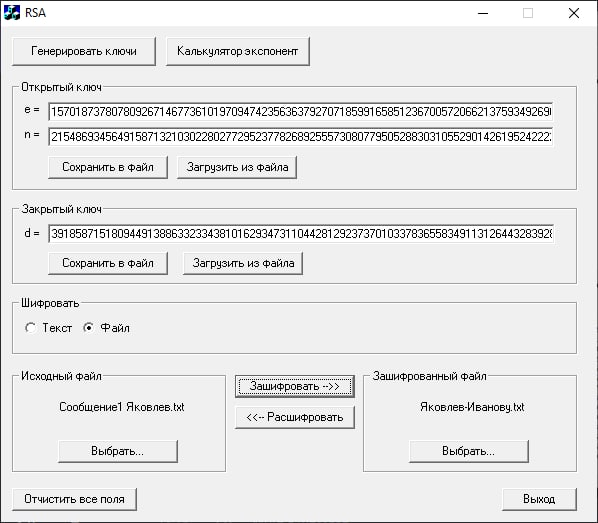
Первое сообщение зашифруем на открытом ключе получателя, предварительно экспортировав его из файла, содержащего этот ключ. Зашифрованному сообщению дадим имя «Яковлев-Иванову». Поместим файл в папку группы.

Открытый ключ Иванова:

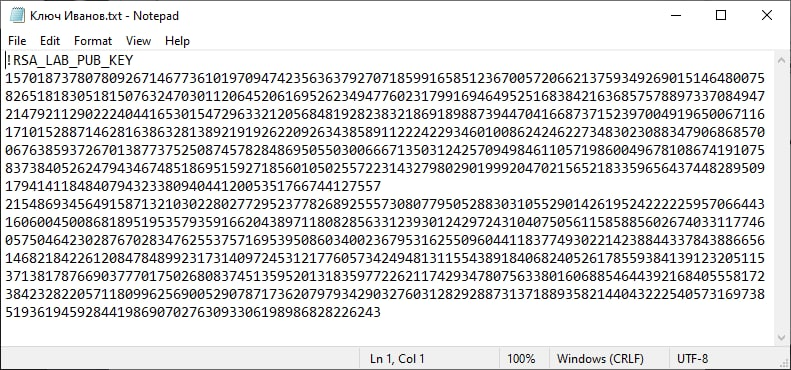
Шифрование сообщения:

Второе сообщение подпишем своим закрытым ключом. Подписанному сообщению дадим имя «Подпись Яковлев».

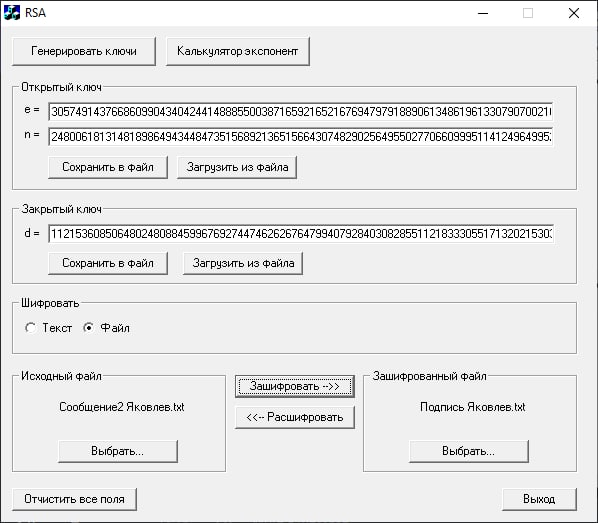
Получатель сообщений на основе своего закрытого ключа расшифровывает зашифрованное первое сообщение и проверяет подпись второго сообщения, используя свой закрытый ключ.

Дешифрование сообщения 1:

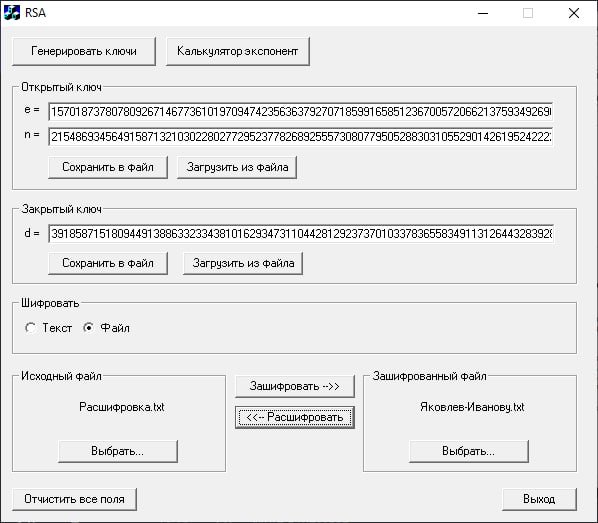
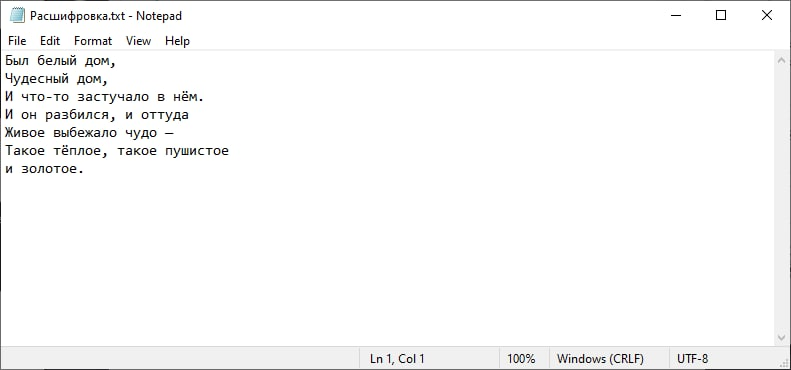
Проверка сообщения 2:

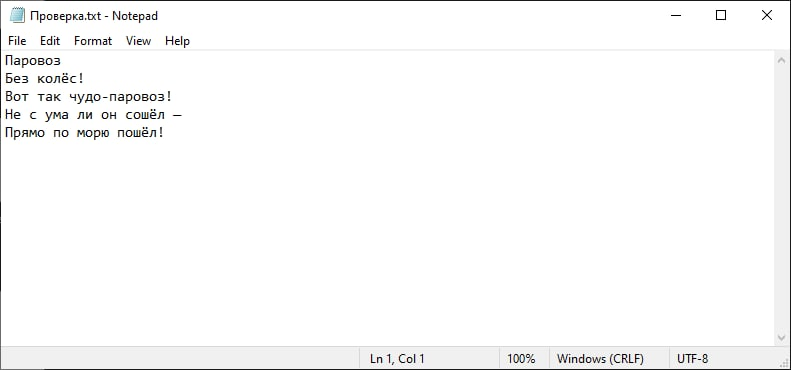
Вывод

В ходе выполнения лабораторной работы были произведены модульные вычисления, генерация ключа в криптосистеме РША, шифрование сообщений, а также безопасный обмен сообщениями в сети.

Санкт-Петербург

2022