МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ

КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Отчет к

лабораторной работе № 4 по дисциплине: «Криптографические методы защиты информации»

Тема: «Изучение подстановочно-перестановочного шифра и его свойств»

Выполнил: ______ (ФИО) (группа) (подпись)

Преподаватель:

Преподаватель: Яковлев В.А. ______ (ФИО) (подпись)

1. Цель лабораторной работы: изучение структуры и основных свойств блочного шифра, основанного на подстановочно-перестановочной сети (Substitution-Permutation Network – SPN), криптоанализ шифра методом тотального перебора ключей, исследование влияния ошибок в канале связи на достоверность расшифрованного сообщения.

2. Используемое программное обеспечение: программа Перебор.exe

3. Порядок выполнения работы

Задание 1. Изучение схемы и принципа действия учебного шифра ППШ.

1. Генерация раундовых ключей

В качестве управляющего 7-битного ключа выберем следующий: 1110110

На основе этого управляющего ключа, сгенерированы 5 раундовых ключей (16-битных последовательностей):

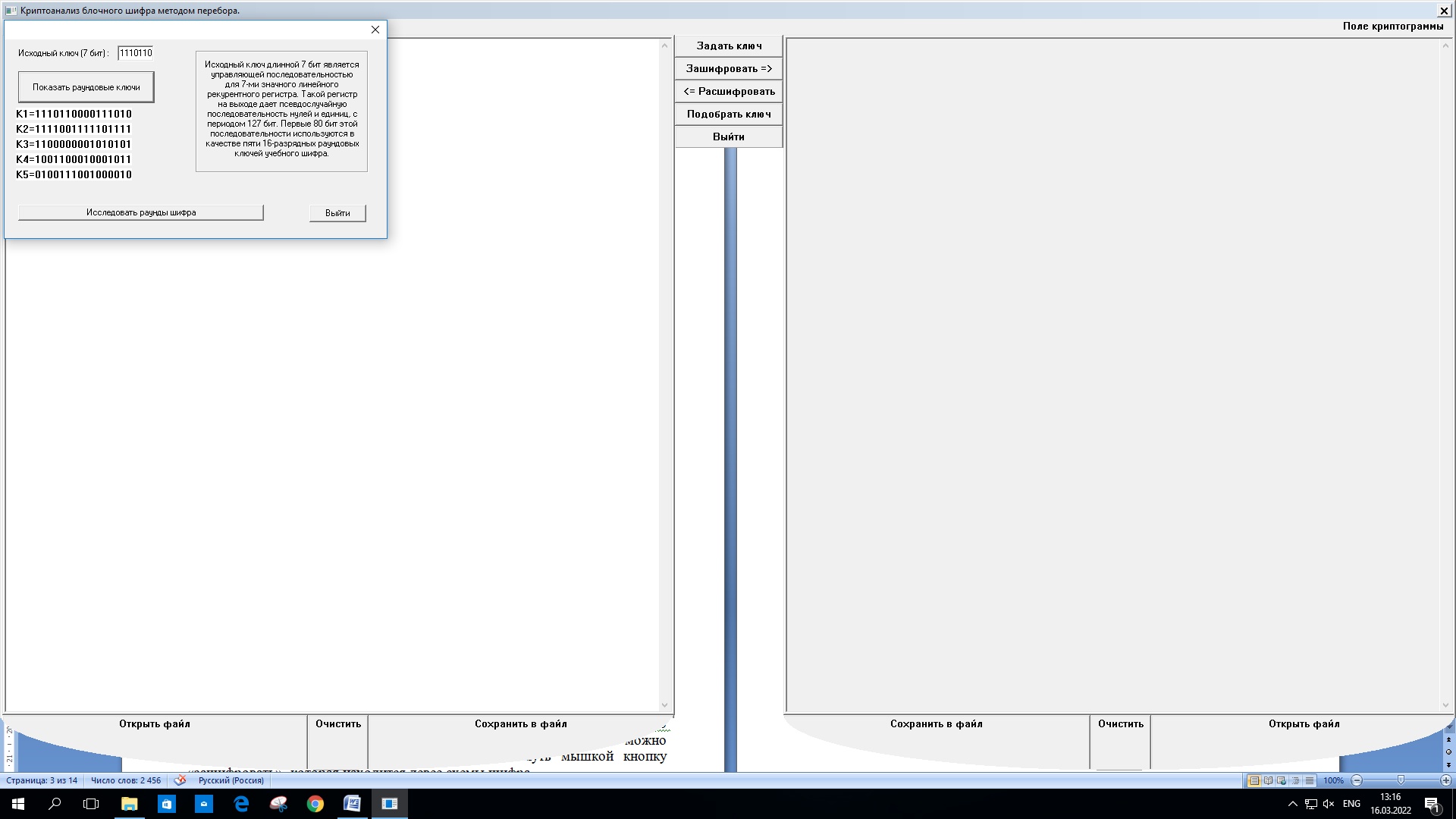
Рисунок 1 – Выбор управляющего ключа, генерация раундовых ключей

K₁ = 1110 1100 0011 1010

K₂ = 1111 0011 1110 1111

K₃ = 1100 0000 0101 0101

K₄ = 1001 1000 1000 1011

K₅ = 0100 1110 0100 0010

2. Анализ преобразований шифра.

Произведем анализ преобразований шифра, выбрав в качестве 16 битной последовательности для шифрования (открытый текст):

1001 1101 1000 1101

Рисунок 2 – Преобразование шифра с промежуточными результатами

Полученная криптограмма: 0001 0111 1100 1101

Раунд 1:

подмешивание ключа: 0111 0001 1011 0111

нелинейное преобразование s-box-ов: 1000 0100 1100 1000

перестановка: 1011 0110 0000 0000

Раунд 2:

подмешивание ключа: 0100 0101 1110 1111

нелинейное преобразование s-box-ов: 0010 1111 0000 0111

перестановка: 0100 0101 1101 0101

Раунд 3:

подмешивание ключа: 1000 0101 1000 0000

нелинейное преобразование s-box-ов: 0011 1111 0011 1110

перестановка: 0101 0101 1111 1110

Раунд 4:

подмешивание ключа: 1100 1101 0111 0101

нелинейное преобразование s-box-ов: 0101 1001 1000 1111

Раунд 5:

подмешивание ключа: 0001 0111 1100 1101

Произведем дешифрование криптограммы, полученной на выходе шифра.

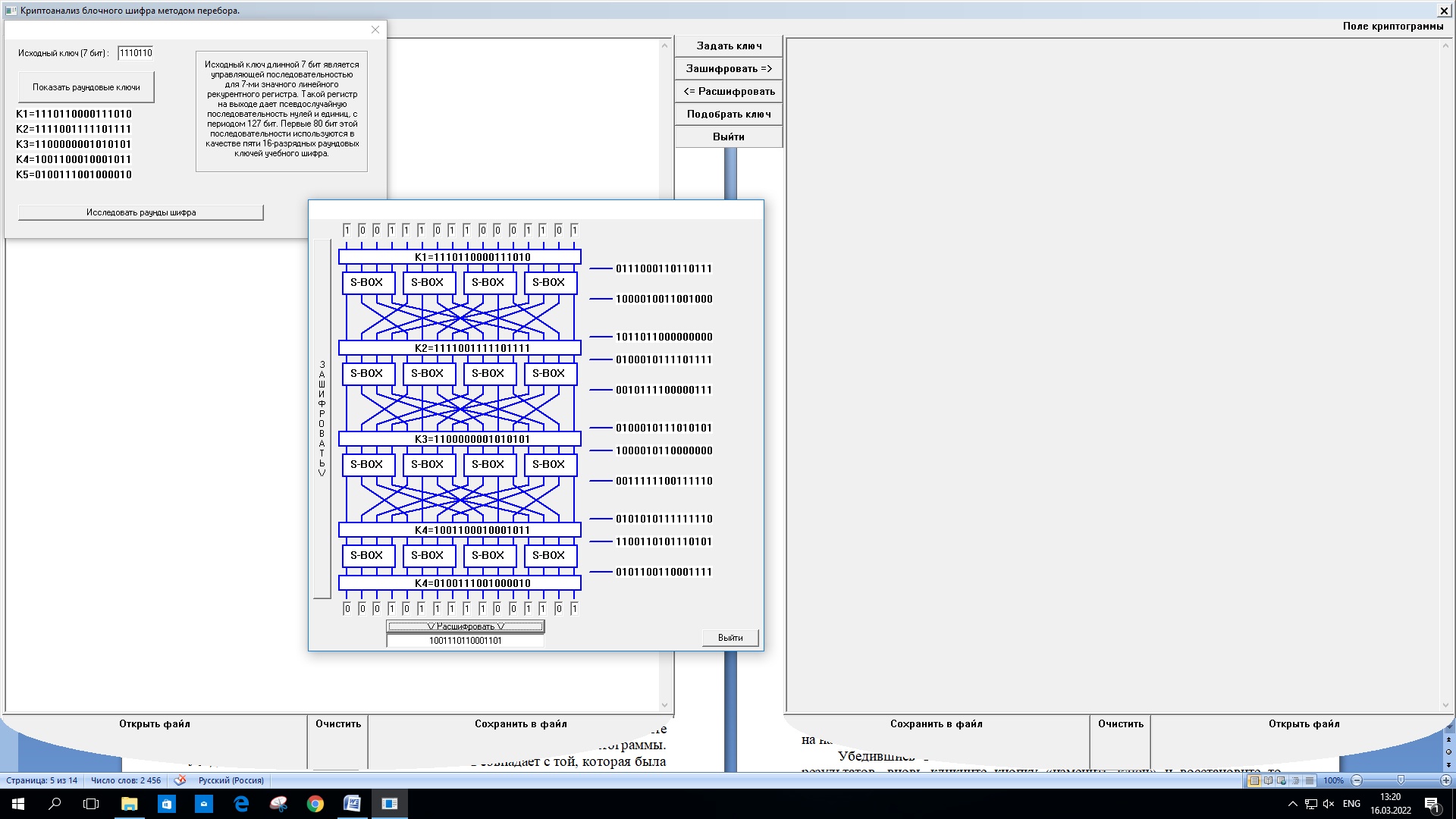
Рисунок 3 – Дешифрование криптограммы

Полученная последовательность совпадает с той, которая была выбрана в качестве «открытого текста» для шифрования.

3. Шифрование сообщения

Произведем шифрование открытого текста с указанием фамилии, для последующей передачи другому студенту в целях криптоанализа:

Рисунок 4 – Открытый текст

Рисунок 5 – Криптограмма

Укажем заведомо неверный ключ и убедимся в неверном дешифровании при его использовании:

Рисунок 6 – Использование неверного ключа для дешифрования.

Рисунок 7 – Неудачная попытка дешифрования при использовании неверного ключа.

Теперь укажем верный ключ и убедимся в верном дешифровании при его использовании:

Рисунок 8 – Использование верного ключа для дешифрования

Рисунок 9 – Удачное дешифрование при использовании верного ключа.

Задание 2. Криптоанализ методом тотального перебора ключей

Рисунок 10 – Полученная криптограмма.

Проведем криптоанализ полученной криптограммы путем перебора всех возможных ключей.

При этом, чтобы не перебирать 2⁷ = 128 ключей, будем учитывать статистику контрольных символов сообщения: «о», «а», «и». Так как в разных текстах, статистика вхождений этих символов может отклоняться от средних значений, будем использовать некоторый доверительный интервал – в случаях, когда под доверительный попадает несколько ключей, доверительный интервал нужно сужать, а когда под доверительный не попало ни одного ключа – наоборот, расширять.

Выберем отклонение от средней частоты – доверительный интервал 8%

Ключ №1 – 0000000:

P(«о») = 0,1%

P(«а») = 0,5%

P(«и») = 0%

Ключ №2 – 0000001:

P(«о») = 0,3%

P(«а») = 0%

P(«и») = 0%

Ключ №3 – 0000010:

P(«о») = 0,1%

P(«а») = 0.3%

P(«и») = 1,5%

Ключ №4 – 0000100:

P(«о») = 0,9%

P(«а») = 0,1%

P(«и») = 0,3%

Ключ №5 – 0000101:

P(«о») = 0,5%

P(«а») = 1,1%

P(«и») = 0,9%

Ключ №6 – 0000110

P(«о») = 0,1%

P(«а») = 0,1%

P(«и») = 0,1%

Как видно, подходящих ключей для доверительного интервала 8% несколько, поэтому сократим доверительный интервал до 5%:

Единственный подходящий ключ – 1010101:

Частоты букв:

P(«о») = 7,22%

P(«а») = 5,8%

P(«и») = 7,2%

Попробуем расшифровать криптограмму указав данный ключ:

Рисунок 11 – Указание подобранного ключа для дешифрования 1000101.

Рисунок 12 – Результат успешного дешифрования криптограммы.

Задание 3. Анализ влияния ошибок в канале связи на достоверность сообщения после его дешифрования.

ППШ является шифром с размножением ошибок – это означает, что в расшифровке криптограммы содержится больше ошибок, чем в самой криптограмме, в которой содержится ошибка.

Вычислим коэффициент размножения ошибок, поочередно посчитав количество ошибок в расшифровке при ошибке в каждом бите криптограммы:

Исходная криптограмма: 0001 0111 1100 1101

Расшифровка криптограммы: 1001 1101 1000 1101

При ошибке в 1-м бите:

Криптограмма с ошибкой: 1001 0111 1100 1101

Расшифровка криптограммы: 0100 1100 1001 1011

Количество ошибок в расшифровке: 10

При ошибке в 2-м бите:

Криптограмма с ошибкой: 0101 0111 1100 1101

Расшифровка криптограммы: 1110 0111 1001 1010

Количество ошибок в расшифровке: 9

При ошибке в 3-м бите:

Криптограмма с ошибкой: 0011 0111 1100 1101

Расшифровка криптограммы: 1001 0101 0111 1011

Количество ошибок в расшифровке: 6

При ошибке в 4-м бите:

Криптограмма с ошибкой: 0000 0111 1100 1101

Расшифровка криптограммы: 1110 0110 0100 0100

Количество ошибок в расшифровке: 10

При ошибке в 5-м бите:

Криптограмма с ошибкой: 0001 1111 1100 1101

Расшифровка криптограммы: 1110 0110 0110 0001

Количество ошибок в расшифровке: 11

При ошибке в 6-м бите:

Криптограмма с ошибкой: 0001 0011 1100 1101

Расшифровка криптограммы: 0001 1100 0011 0001

Количество ошибок в расшифровке: 7

При ошибке в 7-м бите:

Криптограмма с ошибкой: 0001 0101 1100 1101

Расшифровка криптограммы: 1111 1001 0011 1010

Количество ошибок в расшифровке: 9

При ошибке в 8-м бите:

Криптограмма с ошибкой: 0001 0110 1100 1101

Расшифровка криптограммы: 1100 0011 0011 1111

Количество ошибок в расшифровке: 9

При ошибке в 9-м бите:

Криптограмма с ошибкой: 0001 0111 0100 1101

Расшифровка криптограммы: 0011 0000 1100 1100

Количество ошибок в расшифровке: 7

При ошибке в 10-м бите:

Криптограмма с ошибкой: 0001 0111 1000 1101

Расшифровка криптограммы: 1101 1100 0100 0101

Количество ошибок в расшифровке: 5

При ошибке в 11-м бите:

Криптограмма с ошибкой: 0001 0111 1110 1101

Расшифровка криптограммы: 0111 0110 1011 1011

Количество ошибок в расшифровке: 10

При ошибке в 12-м бите:

Криптограмма с ошибкой: 0001 0111 1101 1101

Расшифровка криптограммы: 0011 0011 1001 0010

Количество ошибок в расшифровке: 11

При ошибке в 13-м бите:

Криптограмма с ошибкой: 0001 0111 1100 0101

Расшифровка криптограммы: 0101 1101 0010 1011

Количество ошибок в расшифровке: 6

При ошибке в 14-м бите:

Криптограмма с ошибкой: 0001 0111 1100 1001

Расшифровка криптограммы: 1111 1111 1101 0111

Количество ошибок в расшифровке: 7

При ошибке в 15-м бите:

Криптограмма с ошибкой: 0001 0111 1100 1111

Расшифровка криптограммы: 1101 1101 0000 0111

Количество ошибок в расшифровке: 4

При ошибке в 16-м бите:

Криптограмма с ошибкой: 0001 0111 1100 1101

Расшифровка криптограммы: 1100 0010 0001 0111

Количество ошибок в расшифровке: 12

Подсчитаем среднее количество ошибок:

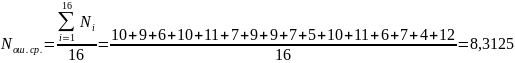
Таким образом, коэффициент размножения ошибок:

4. Вывод: в ходе выполнения лабораторной работы был изучен принцип действия учебного шифра ППШ, произведено шифрование открытого сообщения, рассмотрены результаты преобразований шифра на каждом этапе шифрования, произведен криптоанализ зашифрованного текста, исследована помехоустойчивость шифра при эмуляции ошибок в канале передачи.