
Lab_12_IKB-95
.docxФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем
Кафедра Защищенных систем связи
ОТЧЕТ ПО ЛАБОРТОРНОЙ РАБОТЕ №12
Индексы / Диофантовы уравнения
(тема отчета)
Направление/специальность подготовки
10.03.01 Информационная безопасность
(код и наименование направления/специальности)
Студенты:
(Ф.И.О., № группы) (подпись)
Преподаватель:
Кушнир Д.В.
(уч. степень, уч. звание, Ф.И.О.) (подпись)
Оглавление
Теория…………………………………………………………………………….3
Ход работы……………………………………………………………………….4
Теория
Символ Лежандра.
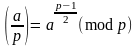
Алгоритм пошагового вычисления символа Лежандра:

Индексы.
Определение. Пусть числа a и b взаимно просты с n, т. е. НОД(a, n) = 1, НОД(b, n) = 1. Число s называется индексом b по модулю n и основанию a, если as ≡ b mod n.
Понятие индекса представляет собой аналогию понятия логарифма. (В дальнейшем часто будет использоваться понятие дискретный логарифм)
В общем случае определение значения индекса (или определения, что его не существует) является сложной задачей.
Один из способов решения – табличный.
Диофантовы уравнения первой степени.
Диофантово уравнение с двумя неизвестными имеет вид:
a x + b y = c,
где a, b, c — заданные целые числа, x и y — неизвестные целые числа.
Найти одно из решений диофантова уравнения с двумя неизвестными можно с помощью Расширенного алгоритма Евклида.
Пусть a и b неотрицательны. Расширенный алгоритм Евклида по заданным неотрицательным числам a и b находит их наибольший общий делитель g, а также такие коэффициенты xg и yg, что:
a * xg + b * yg = g.
Если c делится на g = НОД (a,b), то диофантово уравнение a*x + b*y = c имеет решение; в противном случае диофантово уравнение решений не имеет.
одним из решений диофантова уравнения являются числа:
x0 = xg * (c / g) y0 = yg * (c / g).
Ход работы
Задание 1
Вариант 5: x^2=3 mod 241
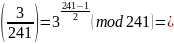 3^120
(mod 241) = 1
3^120
(mod 241) = 1
a/p = (-1)^(120*1)(241/3) 241=3*q+r=3*80+1 241/3 = 1/3 = 1
Вывод: символ Лежандра равен единице, следовательно 3 – квадратичный вычет и уравнение имеет решения.
Задание 2 Вариант 5: а=3, p=23
3^0 = 1 mod 23 3^1 = 3 mod 23 3^2 = 9 mod 23 3^3 = 4 mod 23 3^4 = 12 mod 23 3^5 = 13 mod 23 3^6 = 16 mod 23 3^7 = 2 mod 23 3^8 = 6 mod 23 3^9 = 18 mod 23 3^10 = 8 mod 23 3^11 = 1 mod 23
Таблица индексов
Красный цвет – нет решений
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
Ind3(n) |
0 |
7 |
1 |
3 |
|
8 |
|
10 |
2 |
|
|
4 |
5 |
|
|
6 |
|
9 |
|
|
|
|
Задание 3
Вариант 5: а=13, b=23, c=37 13x + 23y = 37 23 = 13*1 + 10 13 = 10 + 3 10 = 3*3 + 1 3 = 3*1 1 = 10 – 3*3 = 10 – (13 – 10)*3 = (23-13) – ( 13 – (23-13)*3) = 4*23 + 13*(-7) x0 = uc = -7*37 = -259 y0 = vc = 4*37 = 148 x = -259 – 23*t y= 148 +13*t При t = -11 x = -6 y = 5
Санкт-Петербург
2021
