ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

ОТЧЕТ ПО ЛАБОРТОРНОЙ РАБОТЕ №9

Проверка заданного числа

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студенты:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Кушнир Д.В.

(уч. степень, уч. звание, Ф.И.О.) (подпись)

Оглавление

Теория…………………………………………………………………………….3

Ход работы……………………………………………………………………….5

Теория

Тест Рабина-Миллера

Тест Миллера — Рабина — вероятностный полиномиальный тест простоты. Тест Миллера — Рабина позволяет эффективно определять, является ли данное число составным. Однако, с его помощью нельзя строго доказать простоту числа. Тем не менее тест Миллера — Рабина часто используется в криптографии для получения больших случайных простых чисел.

Алгоритм был разработан Гари Миллером в 1976 году и модифицирован Майклом Рабином в 1980 году.

Как и для теста Ферма, все числа m>1, которые не проходят этот тест – составные, а числа, которые проходят, могут быть простыми. Для этого теста нет аналогов чисел Кармайкла. В 1980 году было доказано, что вероятность ошибки теста Рабина-Миллера не превышает 1/4. Таким образом, применяя тест Рабина-Миллера r раз для разных оснований, мы получаем вероятность ошибки 2^−2r.

Число m - 1 однозначно представляется в виде m - 1=2^s∙t, где t нечётно. Целое число a, 1< a < m, называется свидетелем простоты числа m, если выполняются два условия:

1. m не делится на a;

2. a^t ≡ 1 mod m или существует целое k, 0≤ k < s, такое, что:

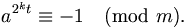
Теорема Рабина утверждает, что составное нечётное число m имеет не более 

φ(m)/4 различных свидетелей простоты, где φ(m) – функция Эйлера.

Алгоритм теста Рабина-Миллера

Алгоритм параметризуется количеством раундов r. Рекомендуется брать r

порядка величины log₂(m), где m — проверяемое число.

Для данного m находят такое целое число s и целое нечётное число t, что m − 1 = 2^s∙t. Выбирается случайное число a,1 < a < m. Если a не является свидетелем простоты числа m, то выдается ответ «m - составное», и алгоритм завершается. Иначе, выбирается новое случайное число a и процедура проверки повторяется. После нахождения r свидетелей простоты, выдается ответ «m, вероятно, простое», и алгоритм завершается.

Алгоритм может быть записан на псевдокоде следующим образом:

Ввод:

число проверяемое на простоту: m > 2 (нечётное натуральное);

параметр, определяющий вероятность ошибки теста r.

Вывод:

составное, означает, что m точно составное;

или вероятно простое, т.е. m с высокой вероятностью является простым.

Представить m − 1 в виде 2^s·t, где t нечётно, можно сделать последовательным делением m - 1 на 2.

цикл А: повторить r раз:

Выбрать случайное a в диапазоне [2, m − 2]

x ← a^t mod m

если x = 1 или x = m − 1 то перейти на следующую итерацию цикла А

для r = 1 .. s − 1

x ← x² mod m

если x = 1 то вернуть составное

если x = m − 1 то перейти на следующую итерацию цикла А

вернуть составное

вернуть вероятно простое

Из теоремы Рабина следует, что если r случайно выбранных чисел оказались свидетелями простоты числа m, то вероятность того, что m составное, не превосходит 4 ^{- r}.

Пример выполнения проверки:

Проверяем число m = 221.

Запишем m − 1 = 220 как (2^2)·55, таким образом s = 2 и t = 55.

Произвольно выберем число a такое, что 1 < a < m-1, допустим a = 174. Переходим к вычислениям:

Шаг 1. a^((2^0)·t) mod m = 174^55 mod 221 = 47 ≠ 1, или m − 1

Шаг 2. a^((2^1)·t) mod m = 174^110 mod 221 = 220 = m − 1.

Так как 220 ≡ −1 mod m, число 221 или простое (174 —свидетель простоты числа 221) или составное, (тогда 174 ложный свидетель простоты).

Возьмём другое произвольное «a», на этот раз выбрав a = 137:

Шаг 1. a^((2^0)·t) mod n = 137^55 mod 221 = 188 ≠ 1, m − 1

Шаг 2. a^((2^1)·t) mod n = 137^110 mod 221 = 205 ≠ m − 1.

Т.е. 221 – составное.

Так как 137 свидетель того, что 221 составное, число 174 на самом деле было ложным свидетелем простоты.

Задание

Выбрать два простых и два составных нечетных числа (не кратных 3 и 5) и еще одно составное число Кармайкла. Выбирать числа для выполнения задания по следующей формуле: 1. Вычисляем: X=((№ студента в группе)+110)*23. Далее произвольно в диапазоне X±20 выбрать нужные числа (если в группе один студент, то проверяем 4-ые числа, если два, то 8, если три то 12). Число Кармайкла выбирать по следующему алгоритму: студент в группе с номером 1. Берёт число 1105 студент в группе с номером 2. Берёт число 1729 студент в группе с номером 3. Берёт число 2465 студент в группе с номером 4. Берёт число 2821 студент в группе с номером 5. Берёт число 6601 студент в группе с номером 6. Берёт число 8911 для студентов с большими номерами выбирать число Кармайкла циклически, 7-й берёт опять число 1105 и т.п. Сколько человек в бригаде, столько разных чисел Кармайкла должно быть проверено.

1. Проверить каждое из чисел тестом Рабина-Миллера. При выполнении задания в EXCEL выбирать k таком образом, чтоб вероятность принять составное за простое была не более 0,0625. При программировании алгоритма выбирать k таком образом, чтоб вероятность принять составное за простое была не более 10^-3.

Ход работы

X = (25+110)*23= 3105

Простые числа – 3119, 3121

Составные числа – 3097, 3113

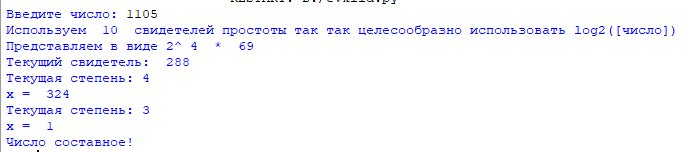
Число Кармайкла – 1105

Алгоритм проверки, реализованный на языке Python3

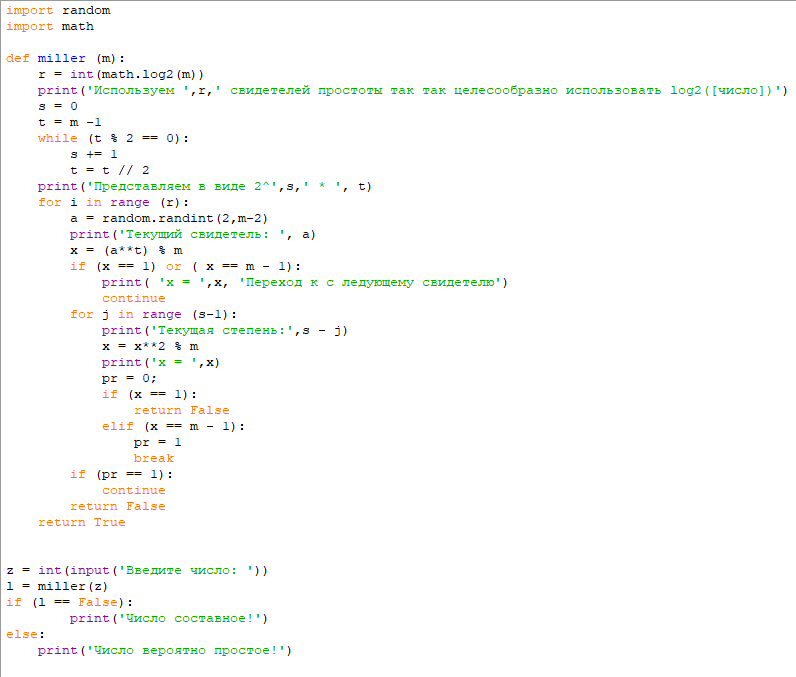
Результат проверки чисел:

3119:

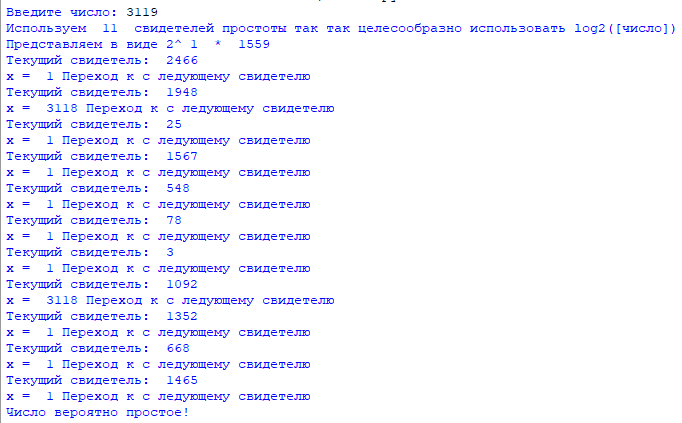
3121:

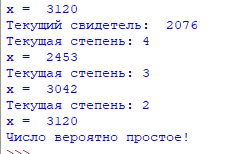
3097:

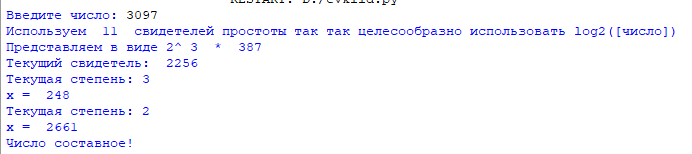
3113:

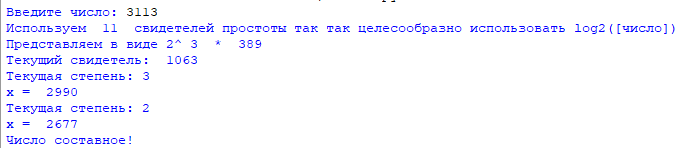
1105:

Санкт-Петербург

2021