
Lab_10_IKB-95
.docxФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем
Кафедра Защищенных систем связи
ОТЧЕТ ПО ЛАБОРТОРНОЙ РАБОТЕ №10
Китайская теорема об остатках
(тема отчета)
Направление/специальность подготовки
10.03.01 Информационная безопасность
(код и наименование направления/специальности)
Студенты:
(Ф.И.О., № группы) (подпись)
Преподаватель:
Кушнир Д.В.
(уч. степень, уч. звание, Ф.И.О.) (подпись)
Оглавление
Теория…………………………………………………………………………….3
Ход работы……………………………………………………………………….4
Теория


Согласно китайской теореме об остатках система уравнений:
x= 1 mod 2 x= 2 mod 3 x= 6 mod 7
Имеет единственное решение на промежутке [0... 2*3*7], если числа 2,3,7 — взаимно простые
Ход работы
Задача 1 (Методом перебора)
Имеется не более 105 кубиков. Их поочерёдно располагают по 3, по 5 или по 7 в ряд. Последний ряд в некоторых случаях оказывается заполненным не полностью (несколько кубиков оказываются «лишними»). По количеству «лишних» кубиков определить их общее количество.
|
Остаток кубиков при раскладывании: |
||
Варианты |
в ряд по 3 |
в ряд по 5 |
в ряд по 7 |
1 |
0 |
0 |
6 |
2 |
0 |
1 |
5 |
3 |
0 |
2 |
4 |
4 |
1 |
3 |
3 |
5 |
1 |
4 |
2 |
6 |
1 |
0 |
1 |
7 |
2 |
1 |
6 |
8 |
2 |
2 |
5 |
9 |
2 |
3 |
4 |
10 |
0 |
4 |
3 |
11 |
0 |
0 |
2 |
12 |
0 |
1 |
1 |
13 |
1 |
2 |
6 |
14 |
1 |
3 |
5 |
15 |
1 |
4 |
6 |
16 |
2 |
0 |
5 |
17 |
2 |
1 |
4 |
18 |
2 |
2 |
3 |
19 |
0 |
3 |
2 |
20 |
0 |
4 |
1 |
Вариант 5. Решение первого уравнения: 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 67, 70, 73, 76, 79. Решение второго уравнения: 4, 9, 14, 19, 24, 29, 34, 39, 44, 49, 54, 59, 64, 69, 74, 79. Решение третьего уравнения: 2, 9, 16, 23, 30, 37, 44, 51, 58, 65, 72, 79.
Задача 2
Спутник1 пролетает над городом в x1 час и имеет период обращения y1 часов.
Спутник2 пролетает над городом в x2 час и имеет период обращения y2 часов.
Спутник3 пролетает над городом в x3 час и имеет период обращения y3 часов.
-
Варианты
x1
x2
x3
y1
y2
y3
1
1
2
3
3
5
7
2
1
3
5
2
3
5
3
2
3
4
3
5
8
4
1
2
4
3
2
5
5
4
4
5
7
2
3
6
5
2
1
7
3
2
7
3
3
1
5
6
7
8
2
4
6
2
5
9
9
2
3
5
3
7
5
10
1
4
2
5
7
3
11
2
3
4
3
5
11
12
2
2
6
2
3
13
13
1
1
7
3
5
11
14
0
2
1
2
7
11
15
1
2
3
7
5
9
16
1
2
3
7
5
9
17
4
3
1
5
7
3
18
5
4
3
6
5
7
19
3
4
5
8
5
9
20
4
5
6
7
8
9
Определить, когда все три спутника пролетят одновременно и как часто это бывает:
Использовать аналитический метод;
Использовать метод, основанный на Китайской теореме об остатках (приведённый на «слайдах»).
Вариант 5.
Аналитический метод:
Составим уравнения, и упорядочим их по возрастанию модуля для удобства:
x = 4 ( mod 2 ) x = 5 ( mod 3 ) x = 4 ( mod 7 )
x = 4+2t 4+2t = 5 mod 3 2t = 1 mod 3 t = 1*(2)(-1) mod 3 t = 2 mod 3 t = 2 + 3u x = 4 + 2t = 4 + 2(2+3u)= 8 + 6u = 2 + 6u 2 + 6u = 4 mod 7 u = 2*6(-1) mod 7 = 2*6 mod 7 = 12 mod 7 = 5 mod 7 x = 2+6u=2+6(5+7v) = 32 + 42v.
Метод, основанный на Китайской теореме об остатках:
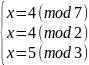 1)
M
= 7*2*3=42
1)
M
= 7*2*3=42
2) M1 = 42/7 = 6 M2 = 42/2 = 21 M3 = 42/3 = 14
3) N1 = 6 N2 = 1 N3 = 2
X = 4*6*6 + 4*1*21 + 5*2*14 = 144 + 84 + 140 = 368 mod 42 = 32 mod 42. Как видим ответ сошелся. Итоговый ответ: спутники пролетят над городом одновременно на 32-часу. Далее это будет происходить через каждые 42 часа.
Санкт-Петербург
2021
