Lab_11_IKB-95

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

ОТЧЕТ ПО ЛАБОРТОРНОЙ РАБОТЕ №11

Квадратичные сравнения

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студенты:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Кушнир Д.В.

(уч. степень, уч. звание, Ф.И.О.) (подпись)

Оглавление

Теория…………………………………………………………………………….3

Ход работы……………………………………………………………………….4

Теория

Частный случай. Сравнение по модулю простого числа p.

x^2=a mod p. (p-простое, a-целое, НОД(a,p)=1).

Такое сравнение имеет либо два решения, либо не имеет решений.

В уравнении

x^2=a mod p, a- называют квадратичным вычетом, если уравнение имеет решения; a- называют квадратичным невычетом, если уравнение не имеет решения. Если p – простое, то (p-1)/2 элементов поля Z_p квадратичные вычеты и (p-1)/2 – квадратичные невычеты.

Символ Лежандра

Определение. Для любого простого нечётного «p» и целого «a» символ Лежандра определяется как:

0, если a=0 mod p = 1, если «a» квадратичный вычет по mod p -1, если «a» квадратичный невычет по mod p

Свойства символа Лежандра (см. лекции)

Алгоритм вычисления символа Лежандра (см. лекции)

Критерий Эйлера. (позволяет определить, является ли число a по mod p квадратичным вычетом или невычетом)

Если a^(p-1)/2 = 1 mod p, то «a» – квадратичный вычет по модулю «p».

Если a^(p-1)/2 = -1 mod p, то «a» – квадратичный невычет по модулю «p».

При составном «n» возможно получение значения a^(n-1)/2 = 0 mod n, что означает, что «a» делит «n» (уравнение не имеет решений).

Т.о. один из способов вычисления символа Лежандра:

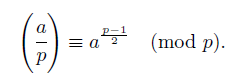
Решение квадратичного сравнения (модуль – простое).

Случай 1. p = 4k+3, т.е. p=3 mod 4, тогда:

X₁= a^(p+1)/4 mod p и X₂= - a^(p+1)/4 mod p

Случай 2. p = 4k+1. (Решение относительно сложное – в данной работе не будет рассмотрено)

Решение квадратичного сравнения (модуль – составной).

Квадратичное сравнение по составному модулю может быть приведено к решению системы сравнений по модулю в виде простого числа. Другими словами, мы можем анализировать x^2=a mod n, если имеем разложение n на множители. Теперь мы можем решить каждое анализируемое уравнение (если оно разрешимо) и найти k пар ответов для x.

Ход работы

Задание 1

p=47, (p-1)/2=23

Зеленый – квадратичный вычет, красный – квадратичный невычет.

Число	Остаток от деления
1	1
2	4
3	9
4	16
5	25
6	36
7	2
8	17
9	34
10	6
11	27
12	3
13	28
14	8
15	37
16	21
17	7
18	42
19	32
20	24
21	18
22	14
23	12
24	12
25	14
26	18
27	24
28	32
29	42
30	7
31	21
32	37
33	8
34	28
35	3
36	27
37	6
38	34
39	17
40	2
41	36
42	25
43	16
44	9
45	4
46	1

Задание 2

4k+1 = 101 4k+3 = 103

Для числа 101.

Числа меньшие половины – 47, 48, 49, 50; Больше половины – 51, 52, 53, 54.

47^2 = 2209 2209 = 88 (mod 101) 48^2 = 2304 2304 = 82 (mod 101) 49^2 = 2401 2401 = 78 (mod 101) 50^2 = 2500 2500 = 76 (mod 101) 51^2 = 2601 2601 = 76 (mod 101) 52^2 = 2704 2704 = 78 (mod 101) 53^2 = 2809 2809 = 82 (mod 101) 54^2 = 2916 2916= 88 (mod 101)

Пример расчёта символа Лежандра для числа 47: a = 76 p = 101

47/101= 7/ 47 = -5 / 7 = -2 / 5 = -2 / 5 = 1 / 5 = 1 Символы Лежандра: Для 47: 1 Для 48: -1 Для 49: 1 Для 50: -1 Для 51: -1 Для 52: 1 Для 53: -1 Для 54: 1 Для числа 103 Числа меньше половины - 48,49,50,51; Больше половины – 52, 53, 54, 55

Число	Квадрат числа	Остаток( mod 103)
48	2304	38
49	2401	32
50	2500	28
51	2601	26
52	2704	26
53	2809	28
54	2916	32
55	3025	38

Символы Лежандра:

Для 48: -1 Для 49: 1 Для 50: 1 Для 51: -1 Для 52: 1 Для 53: -1 Для 54: -1 Для 55: 1 Вывод:

Видно, что для числа вида 4*k+1 числа а повторяются при переходе от чисел меньше половины числа p, к числам больше половины числа p. Символы Лежандра чередуются и “зеркально отражаются” при переходе от чисел меньше половины числа p, к числам больше половины числа p.

В случае числа вида 4*k+3 при переходе числа а “зеркально отражаются”. Символы Лежандра в каждой половине чередуются “два через два”, и при переходе из одной половине к другой эта последовательность “инвертируется”. Задание 3.

p = 47, a = 2; a = 3. x^2 = 2 mod 47 x = ± 2^(47+1/4) mod 47 = ± 7 mod 47 x^2 = 3 mod 47 x = ± 3^(48/4) mod 47 = ± 12 mod 47 Задание 4. n = 133 x^2 = 36 mod 133; 133 = 7*19. x^2 = 36 mod 7 = 1 mod 7 x^2 = 36 mod 19 = 17 mod 19 x = ± 1 mod 7 и x = ± 6 mod 19

Система 1: x = +1 mod 7 и x = +6 mod 19 => x = - 13 = 120 (mod 133) Система 2: x = +1 mod 7 и x = -6 mod 19 => x = -6 = 127 (mod 133) Система 3: x = -1 mod 7 и x = +6 mod 19 => x = 6 Система 4: x = -1 mod 7 и x = -6 mod 19 => x = 13 Ответ: x = ±6 и x = ± 13

Санкт-Петербург

2021