Пример выполнения задачи 12

Условие. На отрезке случайным образом выбраны 162 чисел, точнее, рассматриваются 162 независимых случайных величин, равномерно распределенных на отрезке. Найти вероятность того, что их сумма заключена между 132 и156, т.е..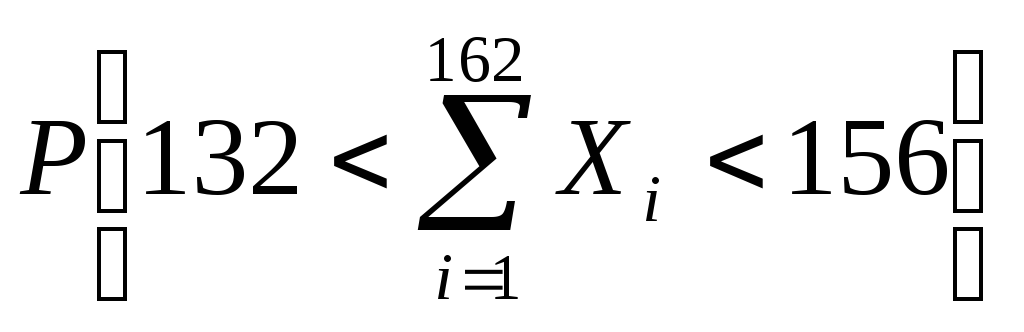

Решение. Так как случайные величины одинаково распределены, то их сумма стремится к нормальному распределению. Следовательно

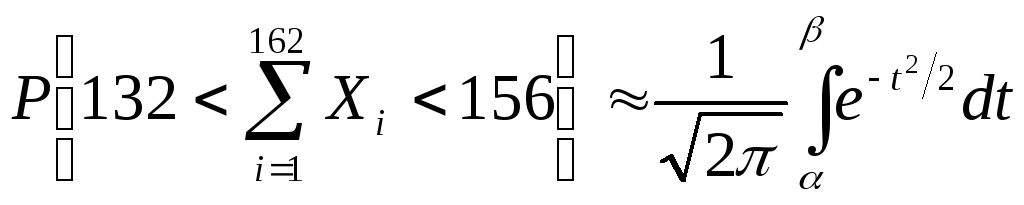и ,

где ,.

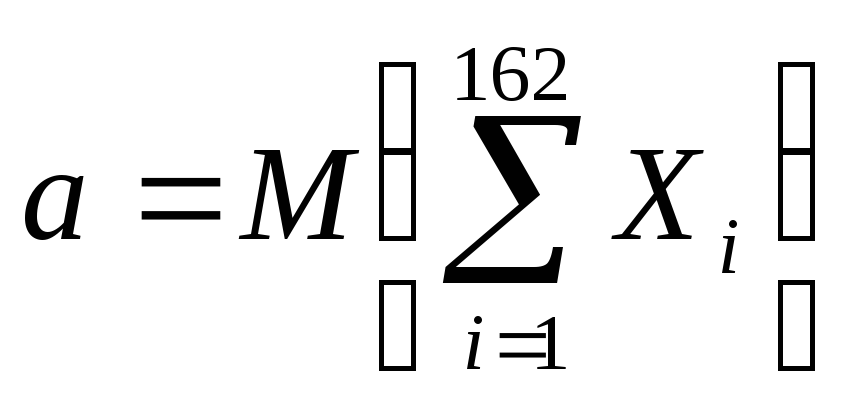Из того, что распределены одинаково, следует, что их числовые характеристики равны, т.е.

, .

Для равномерно распределенной случайной величины имеем

, .

Тогда

,

.

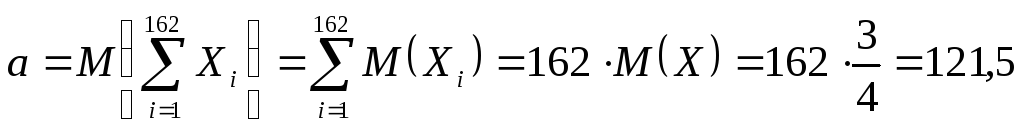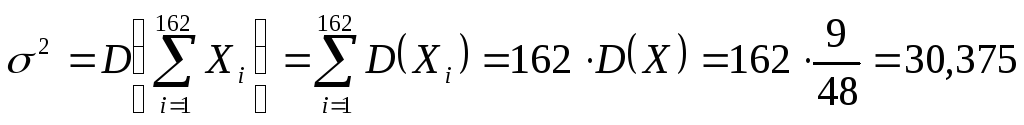Получим

, .

Тогда

.

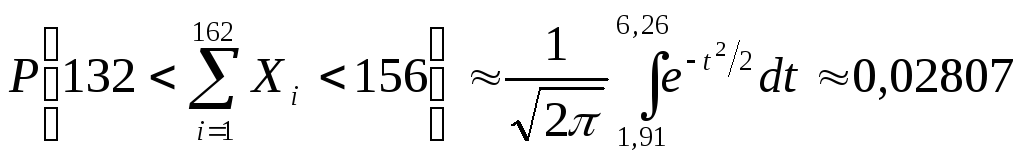Ответ. .

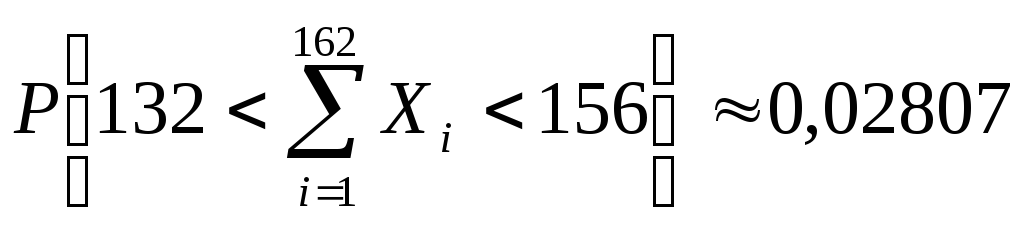Пример выполнения задачи 13

Условие. Случайная величина имеет плотность распределения вероятностей.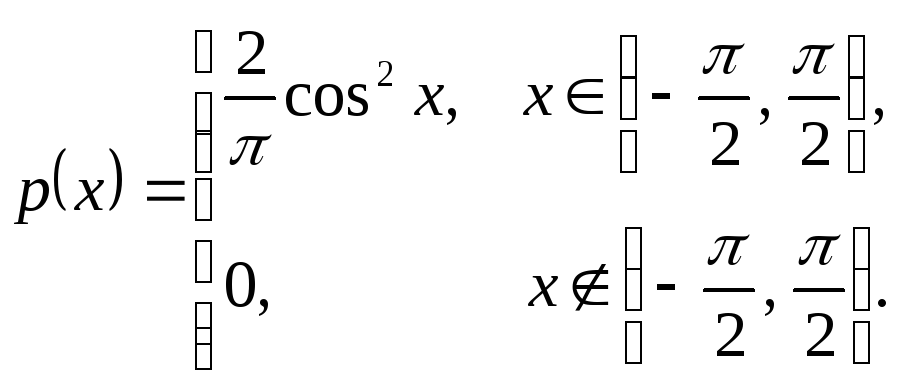

Найти плотность распределения вероятностей случайной величины.

Решение. Функция – монотонная на. Найдем обратную функцию и ее производную:и.

Плотность распределения определяем по формуле.

Тогда .

Определим интервал для . Т. к., то.

Ответ. , при.

Пример выполнения задачи 14

Условие.

Задание 1. По данному графику функции плотности распределения вероятности случайной величины Х (см. рис.1.):

а) определите математическое ожидание случайной величины Х а_х, среднее квадратическое отклонение , медиануМ_е, моду М_о и вероятность попадания случайной величины Х в интервал ;

б) постройте график функции распределения случайной величины F(X).

Задание 2. По данному графику функции распределения случайной величины Х (см. рис.2.):

а) определите математическое ожидание случайной величины Х а_х, среднее квадратическое отклонение , медиануМ_е, моду М_о и вероятность попадания случайной величины Х в интервал ;

б) постройте график функции плотности распределения случайной величины f(X).

,

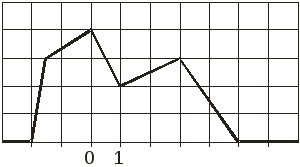
Рис.1.

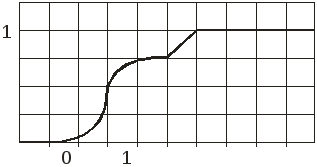
Рис.2.

Решение задания 1. а) Математическое ожидание это среднее значение, которое принимает случайная величина. Поэтому, по рисунку 1 определяем центр масс функции под графиком. Абсцисса этой точки и есть математическое ожидание. .

По правилу трёх сигм имеем: . Значит.

Медиана случайной величины определяется условием: . Вертикальная прямая, делящая площадь фигуры под графиком проходит через точку с абсциссой 1, поэтому.

Мода это наивероятнейшее число. В данном примере имеем двухмодальный случай: .

, где - число клеток, определяющее площадь фигуры на интервале;- число клеток, определяющее общую площадь фигуры..

б) Для построения графика функции будем использовать таблицу 1 связи плотности и функции распределения случайной величины:

Таблица 1

возрастает	выпукла
убывает	вогнута
постоянна	аффинная

а также свойства этих функций. Функция непрерывна на всей числовой прямой и:

выпукла на ;

выпукла на ;

вогнута на ;

выпукла на ;

вогнута на .

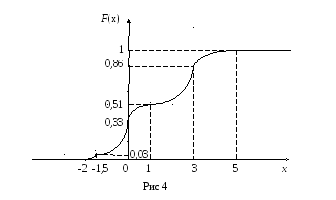
График функции распределения случайной величины изображён на рисунке 4.

Решение задания 2. а) По рисунку 2 случайная величина принимает все свои значения на отрезке и чаще всего на отрезке, поэтому среднее значение равно 1. Значит.

.

, значит .

В точке 1 функция имеет перегиб, значит . В каждой точке отрезкатоже перегиб, значит.

.

б) Для построения графика функции будем использовать таблицу 1, а также свойства плотности и функции распределения случайной величины.

На возрастает, поэтому фигура под графиком будет иметь вид треугольника с высотой равной значению предела функции в точке 1слева. Площадь треугольника равна, поэтому.

На убывает, поэтому фигура под графиком будет иметь вид треугольника с высотой равной значению предела функции в точке 1справа. Площадь треугольника равна, поэтому, а.

На постоянна, поэтому фигура под графиком будет иметь вид прямоугольника с высотой равной значению функции на. Площадь прямоугольника равна, поэтому на.

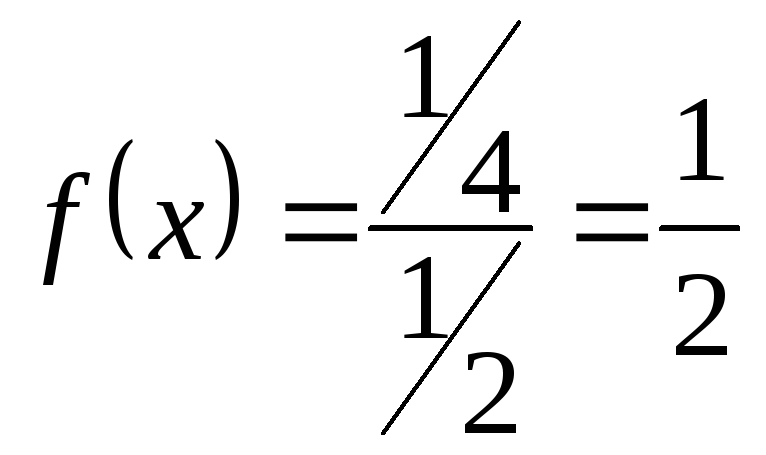График плотности распределения случайной величины изображён на рисунке 5.