Пример выполнения задачи 6

Условие. Вероятность выигрыша в лотерею на один билет равна 0,3. Куплено 13 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.

Решение. Наивероятнейшее число выигрышных билетов определим из неравенств

, где .

Тогда .

Следовательно, наивероятнейшее число выигрышных билетов равно .

Вероятность того, что среди 13 купленных билетов ровно 4 выигрышных определим по формуле Бернулли

.

Ответ. 0,23.

Пример выполнения задачи 7

Условие. При вытачивании гаек наблюдается в среднем 5% брака. Найти вероятность того, что в партии из 250 гаек ровно 230 гаек окажутся не бракованными.

Решение. Вероятность брака равна , тогда вероятность того, что гайка окажется не бракованной, равна. По локальной теореме Лапласа имеем

, где и.

Таким образом, получаем , значение функциивычислим в системеMathCAD. То есть: .

Тогда искомая вероятность равна .

Ответ. .

Пример выполнения задачи 8

Условие. Вероятность наступления некоторого события в каждом из 100 независимых испытаний равна 0,75. Определить вероятность того, что число наступлений события удовлетворяет следующему неравенству

Решение. По интегральной теореме Лапласа имеем

, где .

По условию задачи .

Тогда

, .

Используя MathCAD, получим:

.

Ответ. .

Пример выполнения задачи 9

Условие. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,0012. Поступило 2000 вызовов. Определить вероятность 3 «сбоев».

Решение. Так как число вызовов велико, а вероятность сбоя очень мало, то воспользуемся формулой Пуассона: , где.

По условию имеем . Тогда получим

.

Ответ. 0,21.

Пример выполнения задачи 10

Условие. Найти функцию распределения ДСВ , математическое ожидание, дисперсию, среднее квадратическое отклонение этой случайной величины и вероятность попадания в интервал, если случайная величина задана законом распределения

X	10	11	12	18
P	0,4	0,3	0,2	0,1

Решение. Функция распределения определяется формулой .

Если , то;

если , то;

если , то;

если , то;

если , то.

Получим

Вычислим математическое ожидание

.

Дисперсия равна

.

Найдем среднее квадратическое отклонение

.

Вероятность попадания в заданный интервал определяется формулой

.

Пример выполнения задачи 11

Условие. Дана плотность распределения случайной величины . Найти параметр, математическое ожидание, дисперсию, функцию распределения случайной величины, вероятность попадания в интервал, если

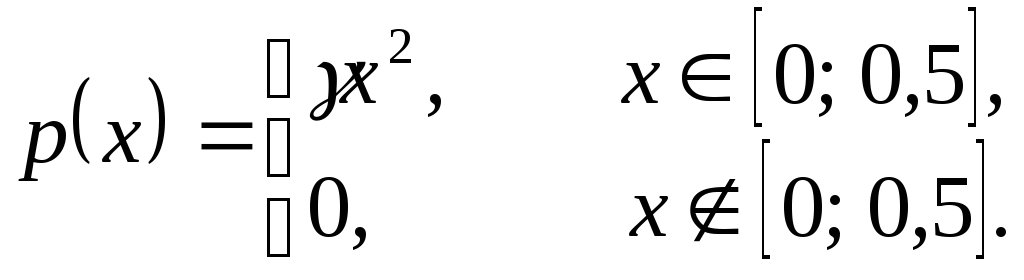
Решение. По свойству плотности распределения вероятностей, имеем

.

Тогда плотность распределения принимает вид

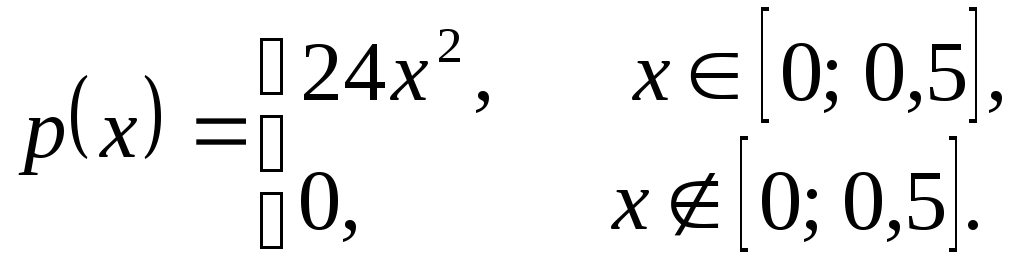
Функция распределения определяется формулой .

Если , то.

Если , то.

Если , то.

Получим

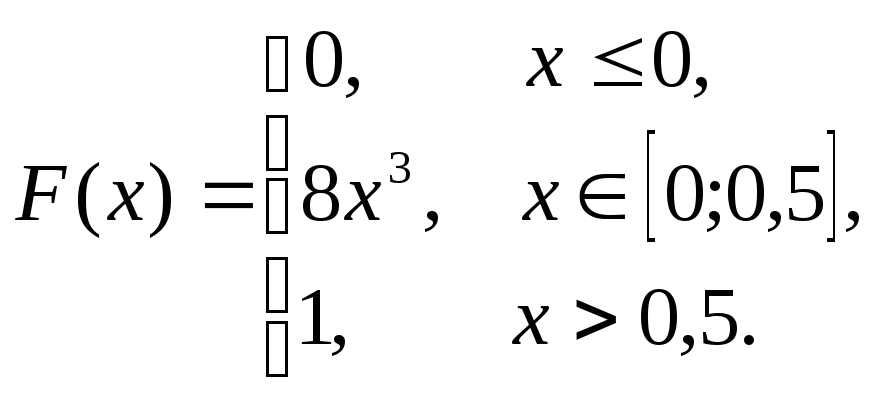
Вычислим математическое ожидание

.

Дисперсия случайной величины равна

.

Найдем вероятность попадания случайной величины в заданный интервал

.