
- •Задачи по теории вероятностей и математической статистике
- •Содержание
- •Введение
- •Раздел 1. Теория вероятностей Комбинаторные формулы
- •Классическое определение вероятности
- •Теоремы алгебры событий
- •Свойства функции распределения
- •Свойства математического ожидания
- •Непрерывная случайная величина и её характеристики
- •Законы распределения случайных величин
- •Предельные теоремы теории вероятностей
- •Предельные формулы для схемы Бернулли
- •Раздел 2. Математическая статистика Обработка результатов опытов
- •Точечные оценки неизвестных параметров и методы их получения
- •Интервальные оценки неизвестных параметров
- •Проверка статистических гипотез
- •Сглаживание опытных данных методом наименьших квадратов
- •Ошибки прямых и косвенных измерений
- •Задания для самостоятельной работы студентов
- •Пример выполнения заданий самостоятельной работы студентов Пример выполнения задачи 1
- •Пример выполнения задачи 2
- •Пример выполнения задачи 3
- •Пример выполнения задачи 4
- •Пример выполнения задачи 5
- •Пример выполнения задачи 6
- •Пример выполнения задачи 11
- •Пример выполнения задачи 12
- •Пример выполнения задачи 13
- •Пример выполнения задачи 14
- •Пример выполнения задачи 15
- •Пример выполнения задачи 16
- •Пример выполнения задачи 17
- •Пример выполнения задачи 18
- •Пример выполнения задачи 19
- •Пример выполнения задачи 20
- •Пример выполнения задачи 21
- •Пример выполнения задачи 22
- •Пример выполнения задачи 23
- •Пример выполнения задачи 24
- •Пример выполнения задачи 25
- •Литература
Точечные оценки неизвестных параметров и методы их получения
Оценка математического ожидания
![]() по выборке
по выборке
![]() .
.
Оценка дисперсии
![]()
Метод максимального правдоподобия
Пусть
![]() заданная выборка случайной величины
заданная выборка случайной величины
![]() ,
имеющей плотность распределения
,
имеющей плотность распределения
![]() ,
где
,
где
![]() - неизвестный параметрический вектор.
Функция
- неизвестный параметрический вектор.
Функция
![]()
называется функцией
правдоподобия.
Оценкой параметрического вектора
![]() ,
полученной методом максимального
правдоподобия называют решение задачи
,
полученной методом максимального
правдоподобия называют решение задачи
![]() .
.
Метод моментов
Оценкой
параметрического вектора
![]() ,
полученной методом моментов называют
решение системы
,
полученной методом моментов называют
решение системы
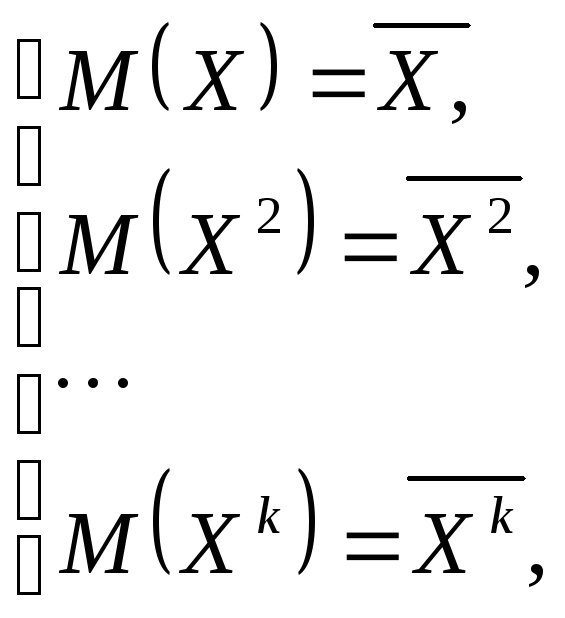
где
![]()
Интервальные оценки неизвестных параметров
Интервал
![]() называется доверительным
интервалом
для оценки параметра
называется доверительным
интервалом
для оценки параметра
![]() ,
отвечающим доверительной
вероятности
,
отвечающим доверительной
вероятности
![]() ,
если
,
если
![]() .
.
Доверительный интервал для математического ожидания
Доверительный интервал для оценки математического ожидания с известной дисперсией
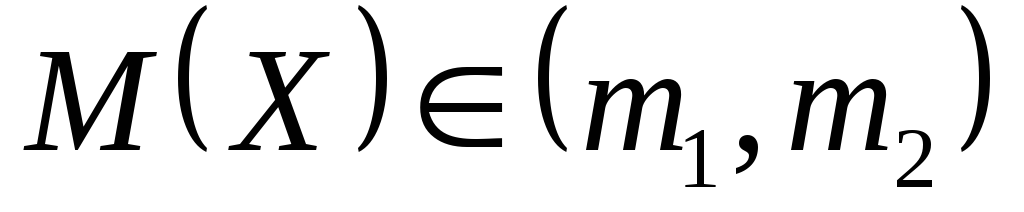 ,
где границы находятся с использованием
MathCAD
по формулам
,
где границы находятся с использованием
MathCAD
по формулам
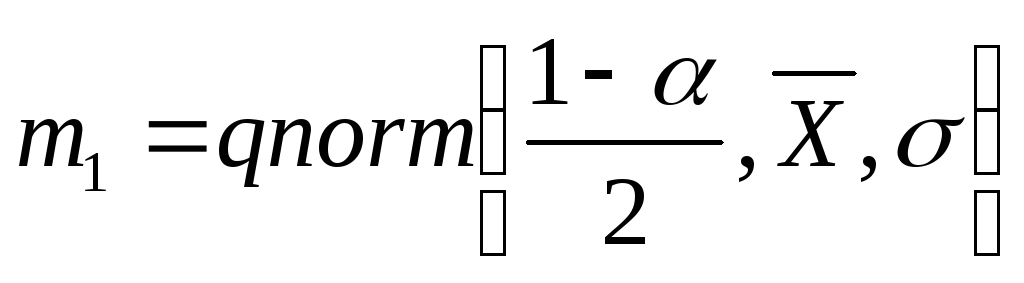 ,
,
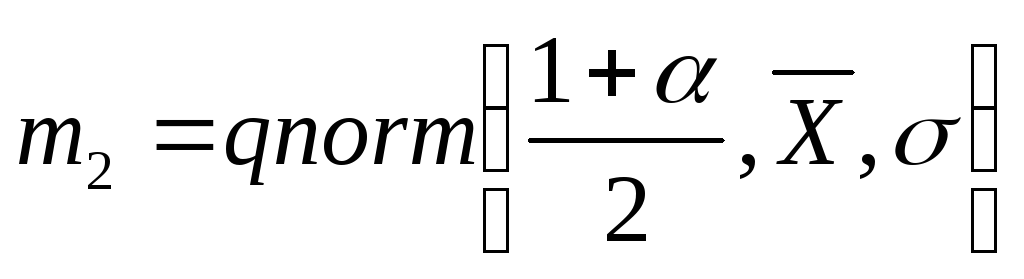 .
.Доверительный интервал для оценки математического ожидания с неизвестной дисперсией
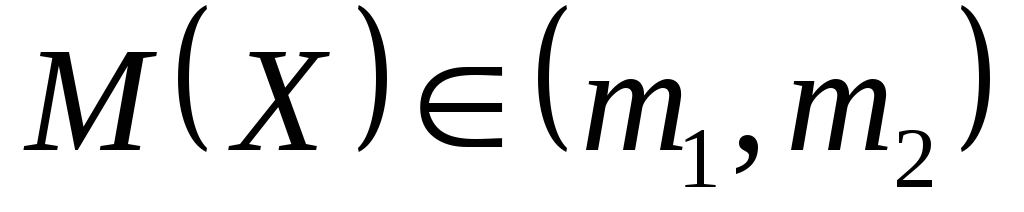 ,
где границы находятся по формулам
,
где границы находятся по формулам
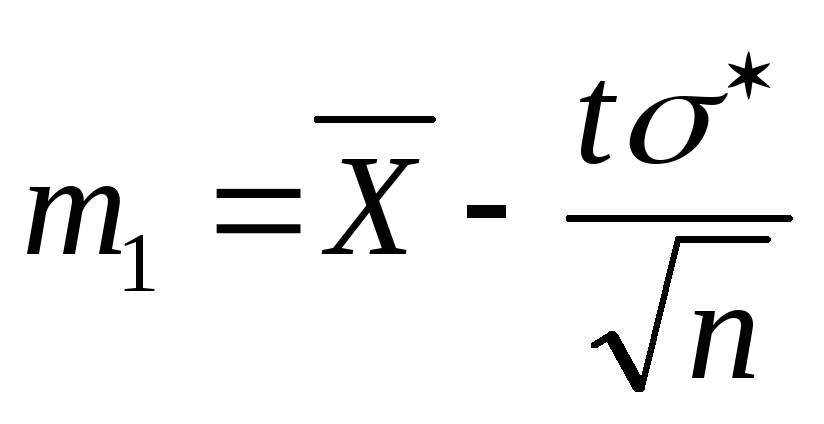 ,
,
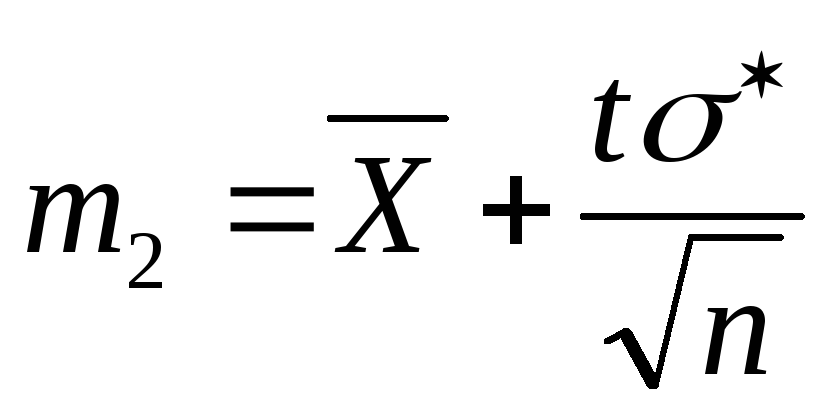 ,
,
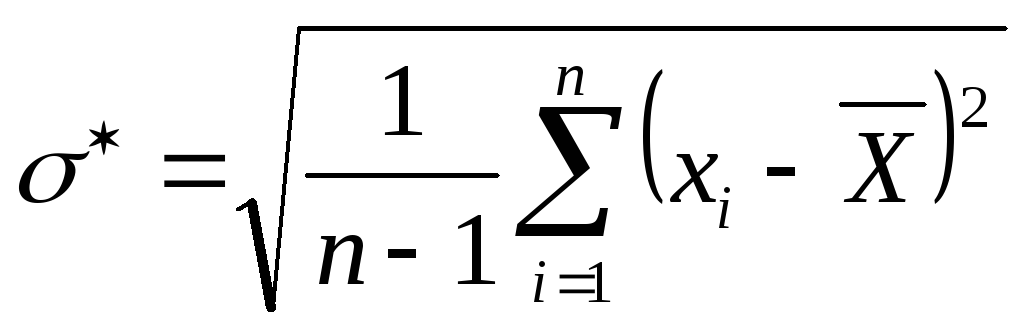 ,
параметр
,
параметр
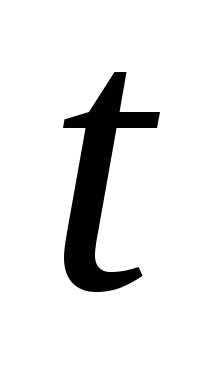 находится с использованием MathCAD
по формуле
находится с использованием MathCAD
по формуле
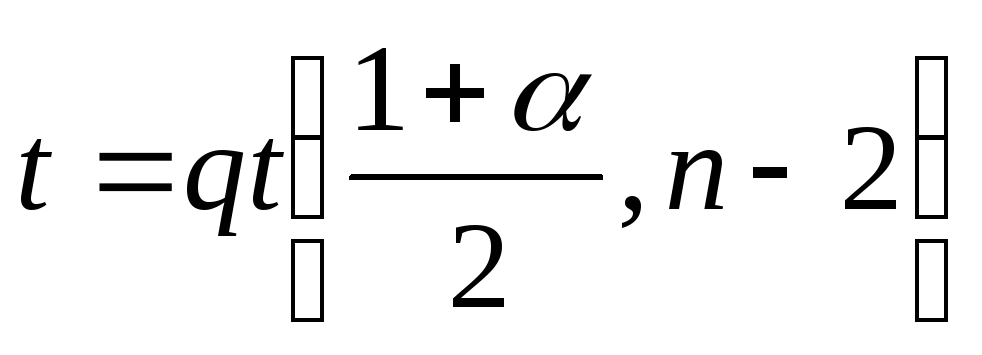 .
.
Доверительный интервал для дисперсии
Доверительный интервал для оценки дисперсии с известным математическим ожиданием
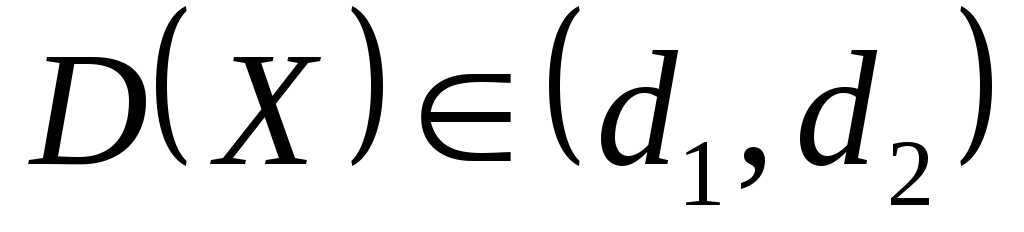 ,
где границы находятся по формулам
,
где границы находятся по формулам
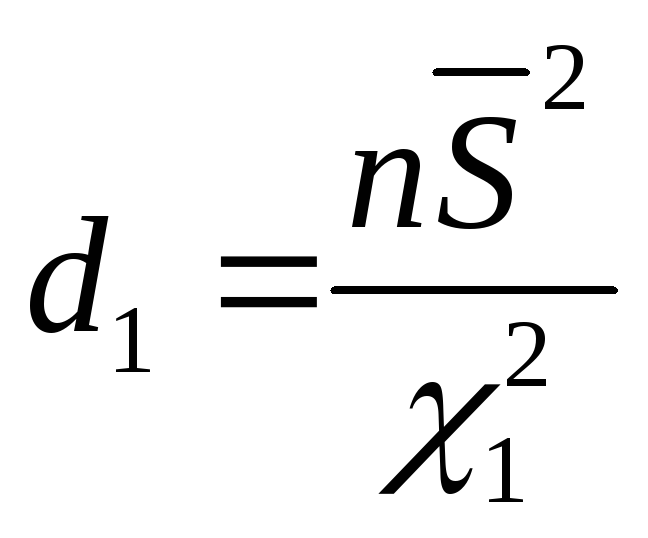 ,
,
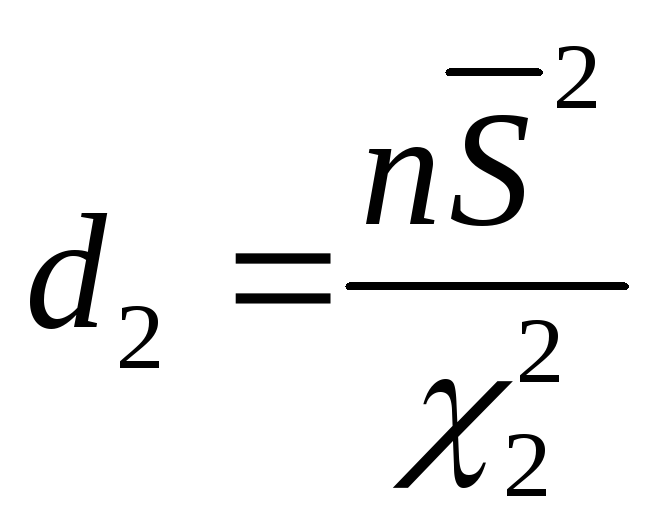 ,
,
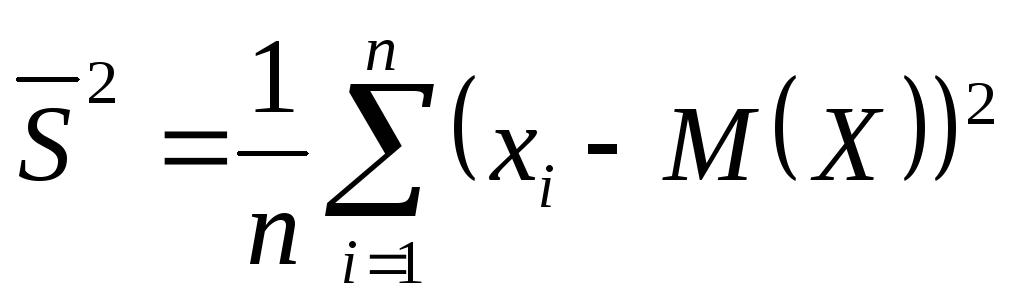 а коэффициенты
а коэффициенты
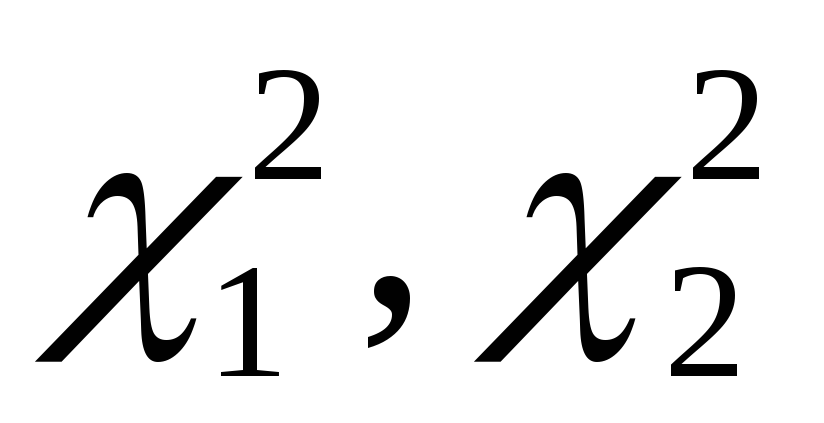 находятся с использованием MathCAD
по формулам
находятся с использованием MathCAD
по формулам
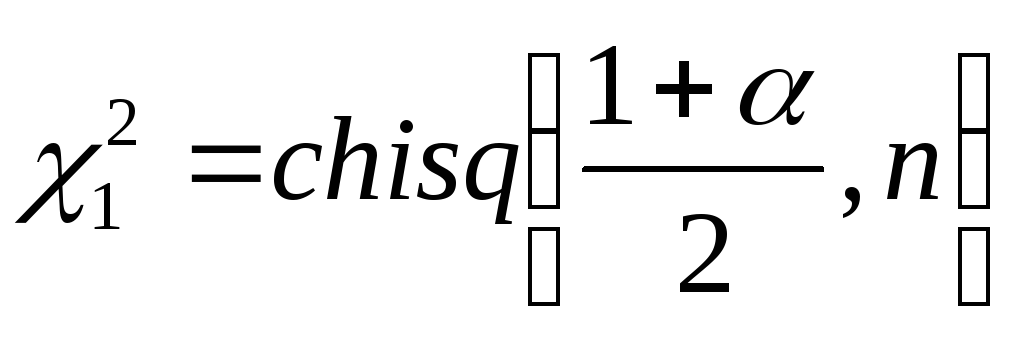 ,
,
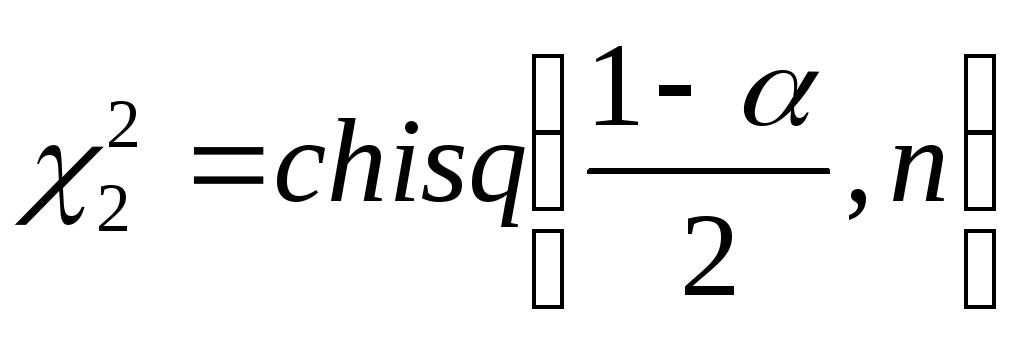 .
.Доверительный интервал для оценки дисперсии с неизвестным математическим ожиданием
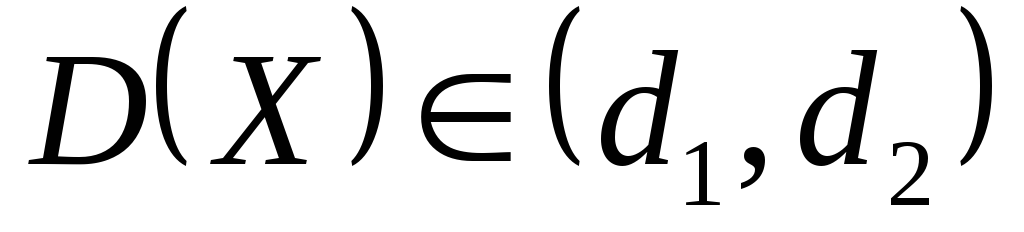 ,
где границы находятся по формулам
,
где границы находятся по формулам
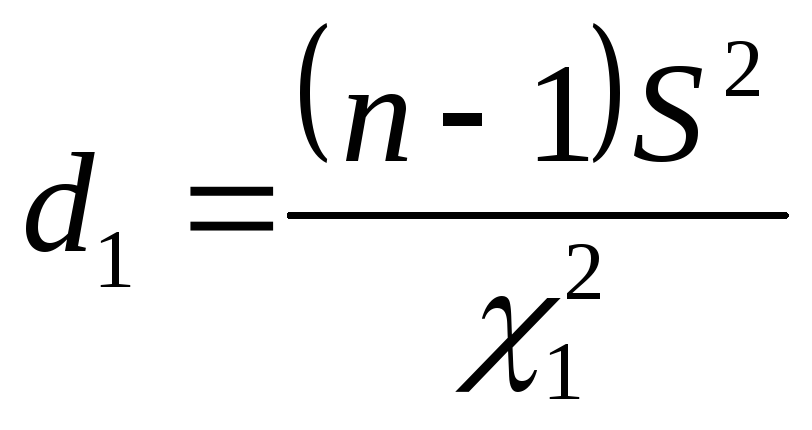 ,
,
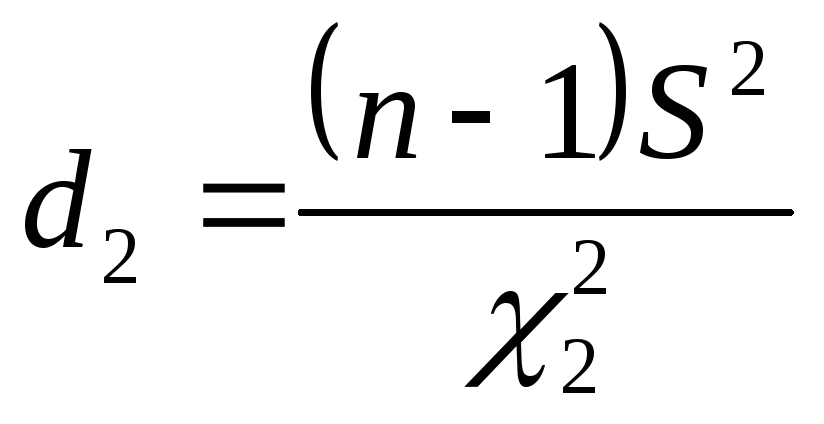 ,
а коэффициенты
,
а коэффициенты
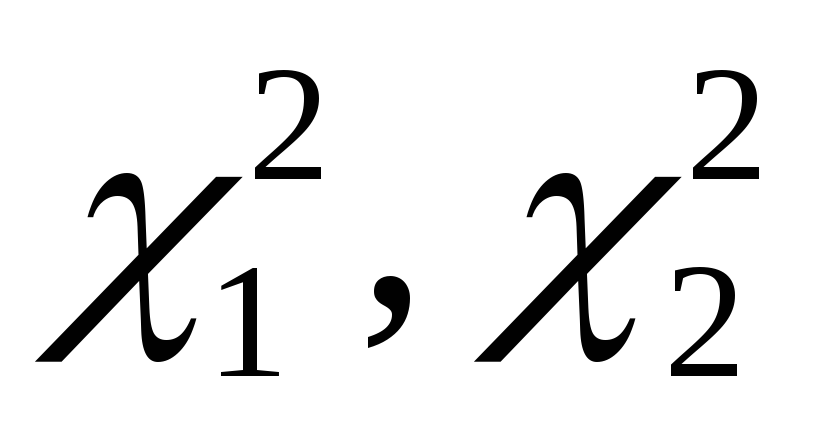 находятся с использованием MathCAD
по формулам
находятся с использованием MathCAD
по формулам
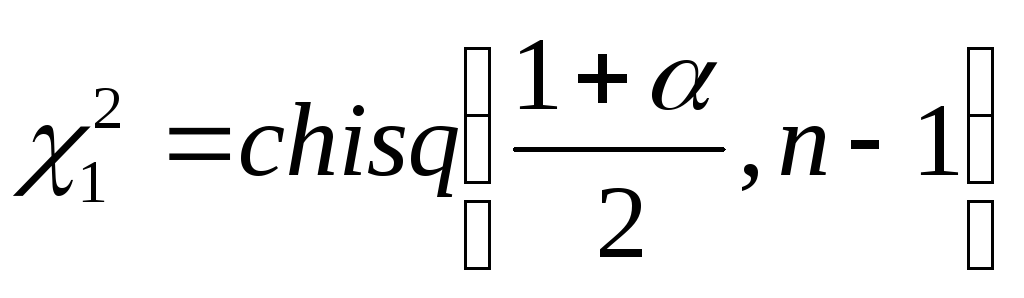 ,
,
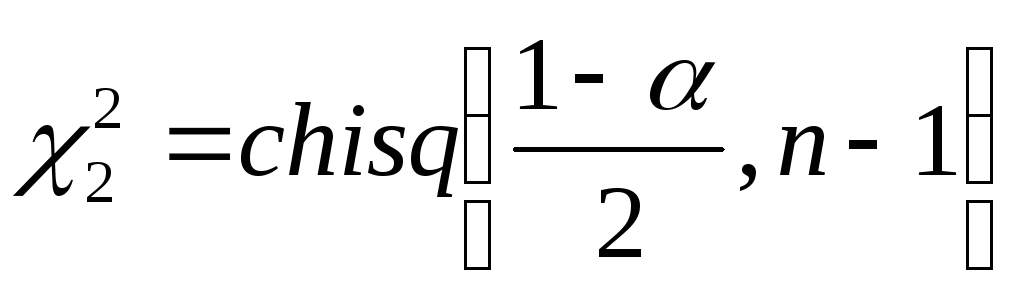 .
.
Проверка статистических гипотез
Критерий
![]()
Проверить гипотезу
о том, что заданная функция
![]() является функцией распределения
случайной величины по выборке
является функцией распределения
случайной величины по выборке
![]() с заданным уровнем значимости
с заданным уровнем значимости
![]() .
.
Уровень значимости это вероятность отвергнуть правильную гипотезу.
Схема проверки
гипотезы по критерию
![]()
Определить по формулам значение
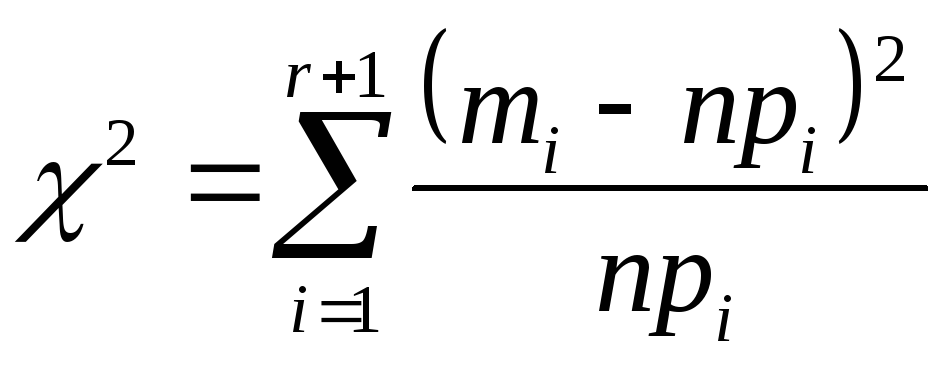 ,
где
,
где
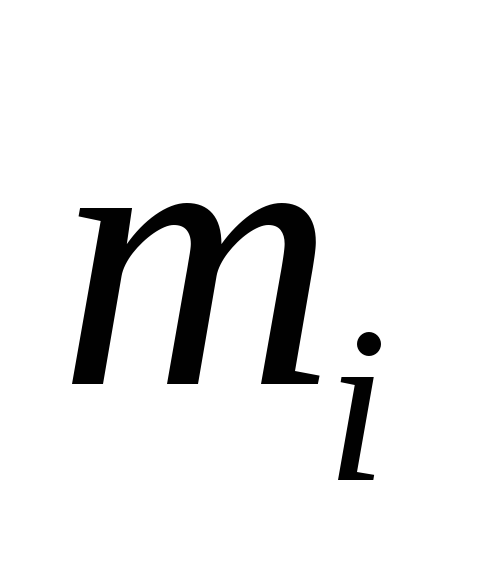 - частота элемента
- частота элемента
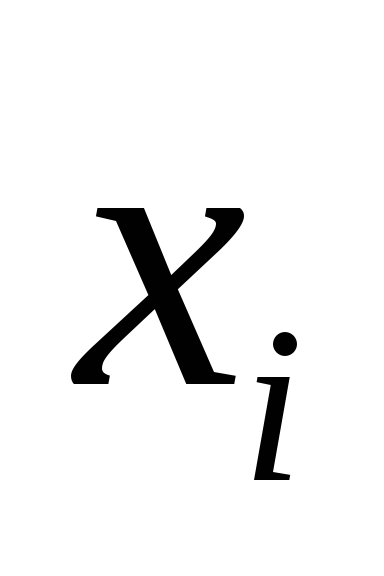 в выборке,
в выборке,
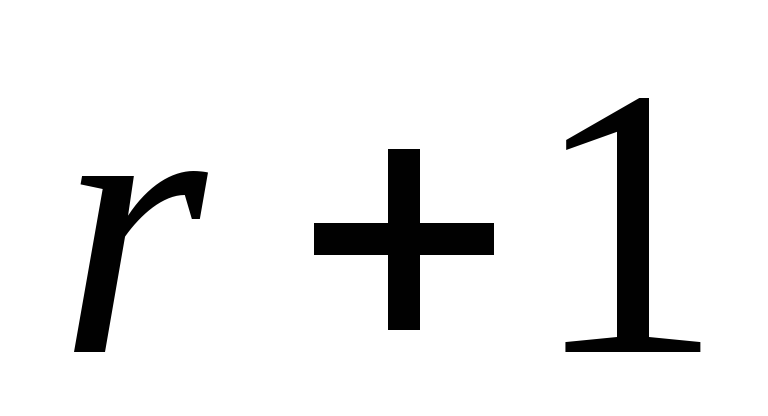 - количество неповторяющихся элементов
выборки,
- количество неповторяющихся элементов
выборки,
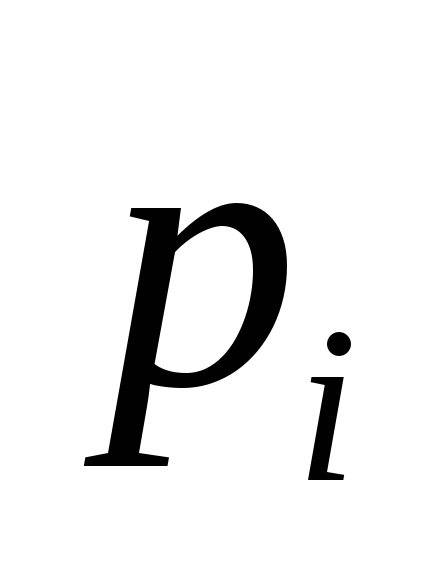 - вероятность появления числа
- вероятность появления числа
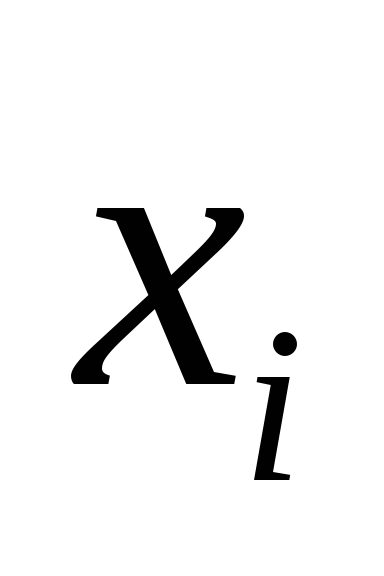 ,
вычисленная по функции распределения
,
вычисленная по функции распределения
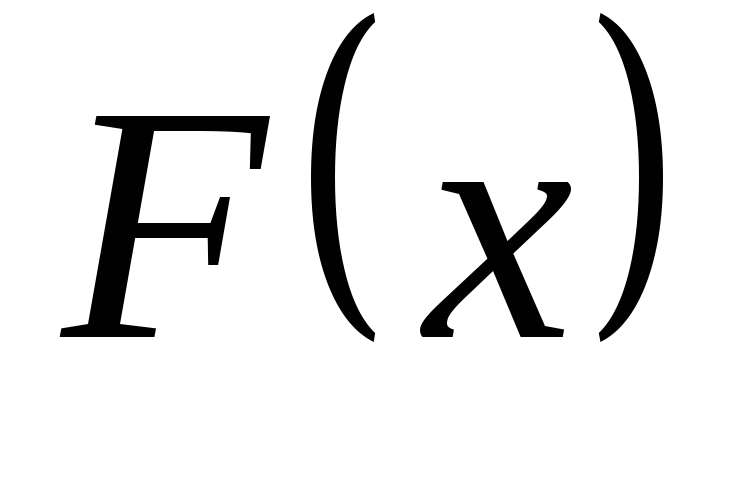 .
.Определить с использованием MathCAD значение
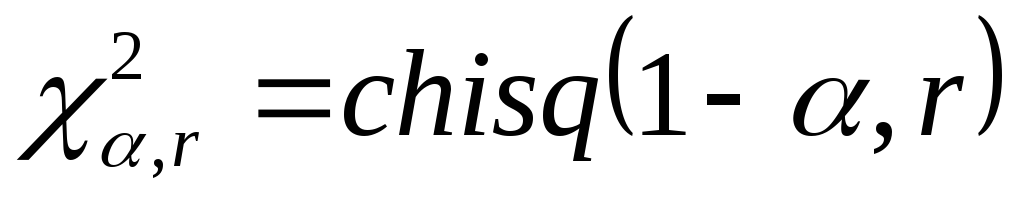 .
.Сделать вывод по правилу:
если
![]() ,
то гипотеза подтверждается;
,
то гипотеза подтверждается;
если
![]() ,
то гипотеза отвергается.
,
то гипотеза отвергается.
Сглаживание опытных данных методом наименьших квадратов
Пусть задана
выборка двумерной случайной величины
![]() Необходимо определить неизвестные
значения параметров
Необходимо определить неизвестные
значения параметров
![]() функциональной зависимости
функциональной зависимости
![]() ,
на основании выборки.
,
на основании выборки.
Согласно метода наименьших квадратов значения неизвестных параметров будем искать, как решение задачи:
![]() ,
,
которая сводится
к решению системы:
![]() .
.
Если зависимость
между переменными линейная
![]() ,
то параметры находятся по формулам:
,
то параметры находятся по формулам:
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
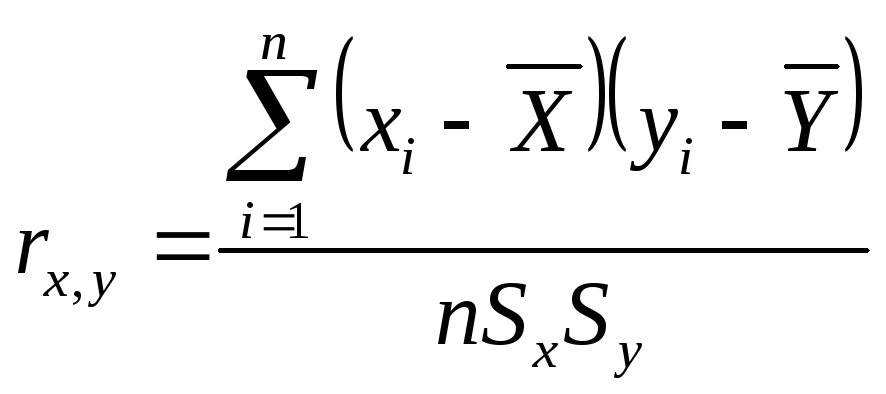 .
.
Ошибки прямых и косвенных измерений
Под прямыми измерениями понимают измерения, полученные непосредственно с помощью прибора.
Под косвенными измерениями понимают результаты, полученные на основе расчёта с использованием прямых измерений.
Если
![]() - точное значение измеряемой величины
- точное значение измеряемой величины
![]() ,
то
,
то
![]() ,
где
,
где
![]() -
ошибка
измерения.
-
ошибка
измерения.
Если при заданной
доверительной вероятности
![]() справедливо
справедливо
![]() ,
где
,
где
![]() - параметр, зависящий от распределения
ошибки и принятой величины доверительной
вероятности
- параметр, зависящий от распределения
ошибки и принятой величины доверительной
вероятности
![]() ,
,
![]() - среднеквадратическая ошибка измерения,
то величина
- среднеквадратическая ошибка измерения,
то величина
![]() называется абсолютной
ошибкой измерения.
называется абсолютной
ошибкой измерения.
Величина
![]() называется относительной
ошибкой измерения.
называется относительной
ошибкой измерения.
Если
![]() величины полученные прямыми измерениями,
то величина
величины полученные прямыми измерениями,
то величина
![]() получена косвенным измерением.
получена косвенным измерением.
Справедливы формулы:
![]() ,
,
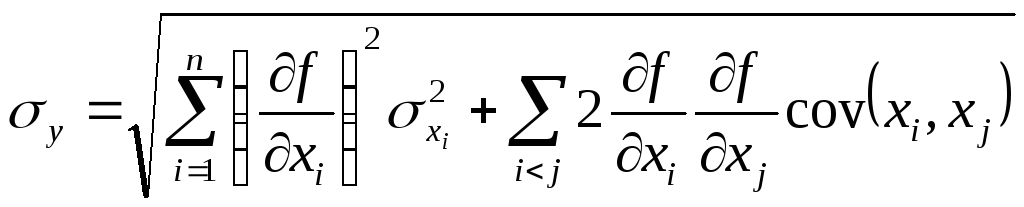 ,
,
где
![]() – ковариация величин
– ковариация величин
![]() .
.
