Пример выполнения задачи 25
Условие. Задание
№1. Дана
зависимость
,
где х и
у измерены
непосредственно. Известно,
что
.
Найти
и
.
Задание №2.
Изобразить прямоугольный треугольник
и отметить на нём три параметра
(две стороны
и угол). Считая, что х
и
у доступны
для измерения, выполнить косвенные
измерения z.
Сравнить с прямым измерением z.
Решение задания1.
Используя свойства математического
ожидания (раздел 1) имеем:
.
Используя формулы раздела 2 имеем:
.
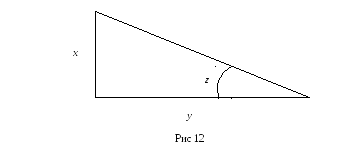
Решение задания2.
На рисунке 12 изображён прямоугольный
треугольник с параметрами:
- катеты,
- угол напротив катета
.
Непосредственным измерением линейкой
и транспортиром, определяем величины
:
,
,
или 0, 384 радиан. Ошибка такого измерения
соответствует четверти деления, значит
,
,
или
0,0044 радиан. Используя правило двух
сигм,
,
где
- точное значение угла
,
имеем:
.
Очевидно
,
значит косвенное измерение
равно:
.
Ошибку косвенного измерения величины
определяем
по формуле:
.
,
,
.
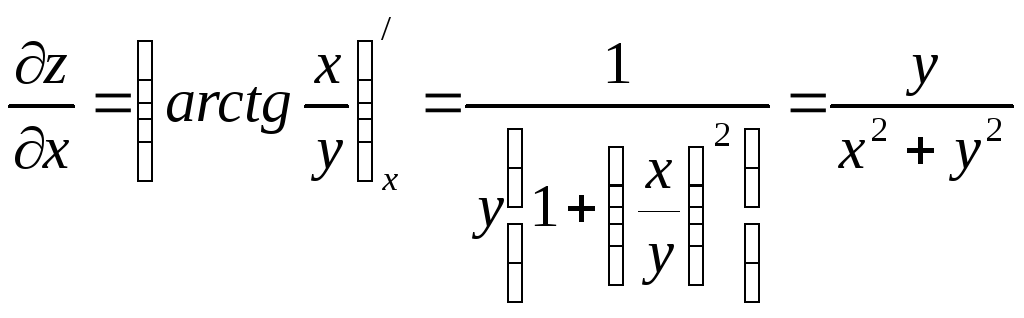Используя правило
двух сигм,
,
имеем:
.
Интервалы для
,
полученные с помощью прямых и косвенных
измерений пересекаются, значит прямые
и косвенные измерения согласуются.
Литература
Вентцель Е.С. Теория вероятностей. Учебник. – М.: Наука; 1969. – 576с.
Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. М.: Академия,2003. – 448 с.
Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. 3-е изд. испр. и доп. – СПб. Издательство «Лань», 2004. – 256 с.
Королев В.Ю. Теория вероятностей и математическая статистика: учеб. - М.: ТК Велби, Изд-во Проспект, 2008. – 160 с.
Семенчин Е.А. Теория вероятностей в примерах и задачах: Учебное пособие. – СПб.: Издательство «Лань», 2007. – 352 с.
Кибзун А.И., Горяинова Е.Р., Наумов А.В. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами: Учеб. Пособие. – М.: ФИЗМАТЛИТ, 2005. – 232 с.
Чистяков В.П. Курс теории вероятностей. – СПб.: Издательство «Лань», 2003. – 272 с.
Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики (типовые расчёты): учебное пособие для ВТУЗов. М.: Высшая школа, 1983. 112 с.