5.Уравнение поверхности уровня и свойства этой поверхности.

Поверхность, в каждой точке которой значение данной функции постоянно, называется поверхностью уровня. Физический смысл функции и ее значения могут быть различными (например, поверхность равной температуры, равного давления и т.п.). В технической механике жидкости наибольший интерес представляет поверхность равного давления, т.е. такая поверхность, в каждой точке которой давление имеет постоянное значение. Так как для поверхности уровня Р = соnst в любой ее точке, dР = 0 и, следовательно, правая часть уравнения также равна нулю. Плотность жидкости отлична от нуля, поэтому выражение в скобках должно быть равным нулю:

- уравнение поверхности равного давления.

Поверхность уровня обладает двумя основными свойствами:

1 . Поверхности уровня не пересекаются между собой. Предположив обратное, мы получим в точках линии пересечения этих поверхностей давлений, равное одновременно Р₁ и Р₂, что физически невозможно. Следовательно, невозможно и пересечение поверхностей уровня.

2. Внешние массовые силы направлены по внутренней нормали к поверхности уровня.

6.Основное уравнение гидростатики, его геометрическая и энергетическая интерпретации.

Поскольку массовой силой является сила тя­жести, ускорением - ускорение свободного падения g, поэтому в вы­бранной системе координат проекции единичной массовой силы на оси Ох, Оу и Оz соответственно будут х = 0, у = 0, z= -g, а уравнение поверхности уровня запишется в следующей форме:

Таким образом, поверхностью уровня (поверхностью равного давления) в однородной покоящейся жидкости будет любая горизонтальная плоскость, в том числе и свободная поверхность, независимо от формы сосуда или водоема. Горизонтальной плоскостью будет также граница раздела двух несмешивающихся жидкостей.

Если в форму­лу основного диф. уравнения равновесия жидкости подставить значения х = 0,у =0 и z= -g, то получим:

После интегрирования и деления на ρg получим:

- основное уравнение гидростатики.

z – нивелирная высота

Р/ρg – приведенная высота

Н – гидростатический напор.

Это уравнение выражает закон распределения гидростатического давления в покоящейся жидкости, согласно которому гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.

Для двух произвольных горизонтальных плоскостей 1 и 2 уравнение примет вид:

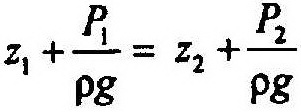
Для определения постоянной интегрирования рассмотрим равнове­сие жидкости в сосуде произвольной формы со свободной поверхно­стью. Давление в каждой точке на свободной поверхности Р = Р₀, расстояние от

произвольной плоскости сравнения до свободной поверхности равно z_0.

Т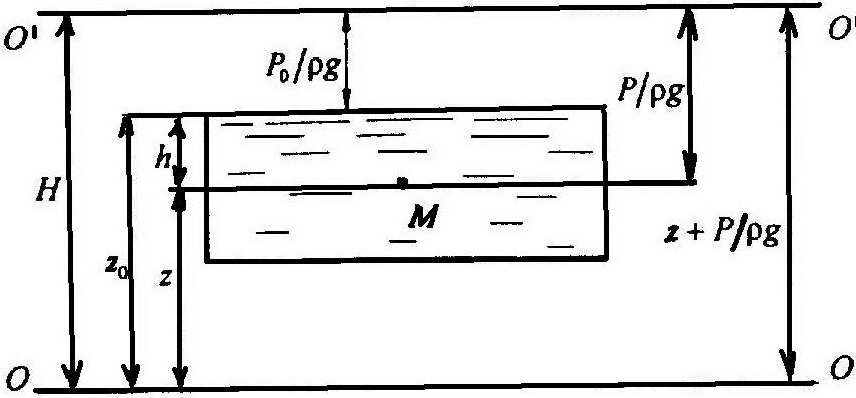 огда

и

или

Размерность отметок z₀ – z = h представляет глубину погружения точки М:

- основное уравнение гидростатики в форме давлений.

Р – полное (абсолютное) гидростатическое давление.

Р₀ – внешнее давление (давление на свободную поверхность).

Геометрическое и энергетическое толкование основного уравнения равновесия жидкости.

Р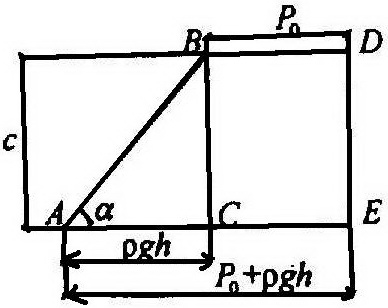 аспределение гидростатического давления по вертикали линейно зависит от глубины погружения рассматриваемой точки и может быть графически представлено в виде трапеции АВДЕ для полного давления или прямоугольного треугольника АВС для избыточного давления. Отметим, что котангенс угла наклона линии давления АВ прямо пропорционален плотности жидкости.

Р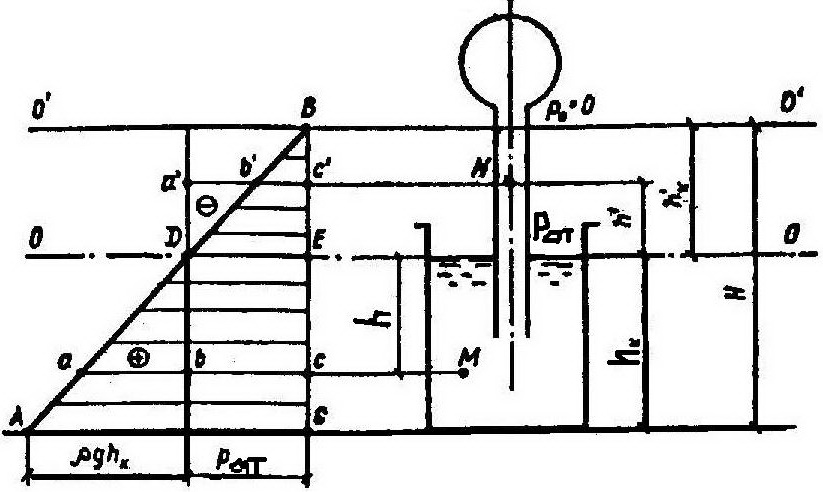 ассмотрим равновесие жидкости в открытом сосуде. Предположим, что вдоль поверхности уровня 0-0 внешнее давление равно атмосферному, вдоль О'-О' - нулю. Тогда изменение полного давления по вертикали графически будет изображаться треугольником АВС. В вершине В этого треугольника полное давление равно нулю, на глубине Н оно будет Р=ρgh или, учитывая, что вдоль линии 0-0 дав­ление атмосферное, Р = Р_атм+ ρgh_к (где h_к - полная глубина жидкости в сосуде). Проведем вертикаль через точку О до пересечения с линиями О'-0' и АС. Треугольник АВС делится на две части, одна из которых (трапеция АДЕС) определяет полное давление ниже линии 0-0, другая выше линии 0-0. Выберем внутри рассматриваемой жидкости две точки М и N так, чтобы одна из них (М) находилась ниже, а другая (N)выше поверхно­сти уровня 0-0. Определим давление в этих точках с помощью графика распределения давления. Полное давление в точке М определится отрезком ас, причем внешнему давлению будет соответствовать отрезок bс, избыточному - отрезок аb. Давление в точке N можно представить в виде разности отрезков а'с' и а'b'. В обоих случаях атмосферное давление соответствует отрезкам а'с' = bс или Р_атм= а'с' =bс. В результате имеем:

где h и h' - расстояния соответственно от точек М и N до поверхности уровня Р = Р_атм. Таким образом, в общем виде можно записать:

Из последних уравнений следует, что в графической интерпретации избыточное давление может быть как положительным, так и отрицательным, в то время как полное Р и внешнее Р_атм - величины сугубо положи­тельные. В общем случае полное давление может быть больше или меньше атмосферного. Если Р < Р_атм, разность между атмосферным и полным давлением называется вакуумом, или вакуумметрическим давлением. Если Р > Р, избыточное давление называется манометрическим. И тогда:

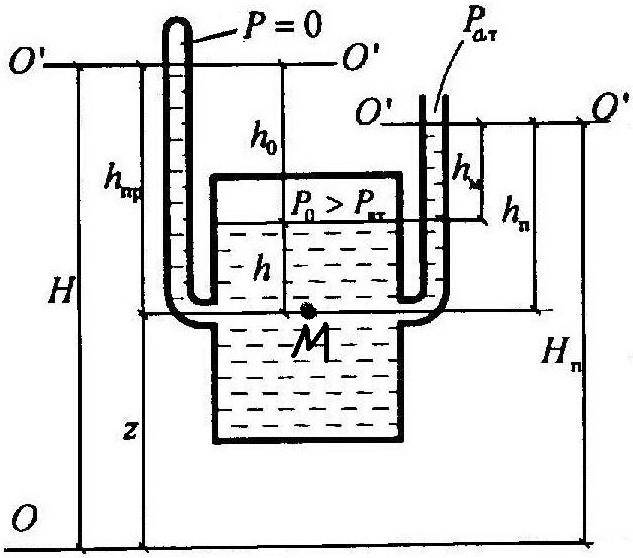
Слагаемые основного уравнения гидростатики имеют линейную размерность, поэтому его легко представить в виде суммы двух отрезков, равных z и Р/ρg. Величина z в технической механике жидкости называется высотой положения, она отсчитывается от произвольной плоскости сравнения 0-0, поэтому z - величина произвольная. Величина Р/ρg определяется давлением в рассматриваемой точке (М) и может быть

измерена высотой h_пр подъема жидкости в присоединенной к сосуду трубке, из которой полностью удален воздух. Если трубка откры­тым концом соединена с атмосферой (такая трубка называется пьезо­метром), то высота подъема жидкости будет определяться манометрическим или избыточным давлением. Высота h_п называется пъезометрической высотой.

В ысота h_пр называется приведенной высотой.

С умму высот Н называют гидростатическим напором.

Гидростатический напор для всех точек покоящейся жидкости есть величина постоянная.

Произведение h_пр·mg – есть потенциальная энергия, которая способна произвести работу по перемещению массы m из точки М в плоскость гидростатического напора. Таким образом из основного уравнения гидростатики следует, что сумма удельной потенциальной энергии положения z и удельной потенциальной энергии гидростатического давления Р/ρg есть величина постоянная для всех точек покоящейся жидкости.