Вопрос 20!

СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ

И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ

Теорема 1.Если функцияf(x)является бесконечно большой приx→a, то функция 1/f(x)является бесконечно малой приx→a.

Доказательство.Возьмем произвольное число ε>0и покажем, что при некоторомδ>0(зависящим от ε) при всехx, для которых|x – a|<δ, выполняется неравенство, а это и будет означать, что1/f(x) – бесконечно малая функция. Действительно, так какf(x)– бесконечно большая функция приx→a, то найдетсяδ>0такое, что как только|x – a|<δ, так |f(x)|>1/ε. Но тогда для тех жеx.

Примеры.

1. Ясно, что при x→+∞ функцияy=x²+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция– бесконечно малая приx→+∞, т.е..

2. .

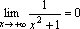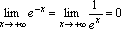Можно доказать и обратную теорему.

Теорема 2.Если функцияf(x)- бесконечно малая приx→a(илиx→∞)и не обращается в нуль, тоy=1/f(x)является бесконечно большой функцией.

Доказательство теоремы проведите самостоятельно.

Примеры.

1. .

2. .

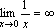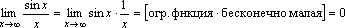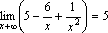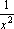3. , так как функциии- бесконечно малые приx→+∞, то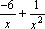, как сумма бесконечно малых функций есть функция бесконечно малая. Функция же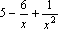является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство.

Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0

.

Вопрос 21!

Бесконечно малая функция.

Рассмотрим функцию, определенную в некоторой окрестноститочки,,  за исключением, быть может, самой точки. Функцияназываетсябесконечно малойпри, стремящемся к, если. Если— бесконечно малая в точке, то для любого положительного числа, как бы мало оно ни было, существует такое положительное число, что для всех, удовлетворяющих неравенству, справедливо неравенство. Неравенствадля всех, эквивалентные неравенствам,, означают, что для любогосуществует такое, что дляграфик функции расположен на плоскости в прямоугольнике. Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию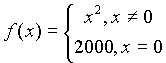.  Приx, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно,пределравен нулю и функция является бесконечно малой.

ПРИМЕР 1. Бесконечно малые функции

Сравнение бесконечно малых функций.

Пусть и— две функции, бесконечно малые в точке. Если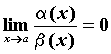, то говорят, чтоболее высокого порядка малости, чеми обозначают. Если же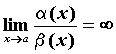, тоболее высокого порядка малости, чем; обозначают. Бесконечно малые функциииназываются бесконечно малыми одного порядка малости, если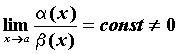, обозначают.  И, наконец, еслине существует, то бесконечно малые функцииинесравнимы.

ПРИМЕР 2.  Сравнение бесконечно малых функций

Эквивалентные бесконечно малые функции.

Если 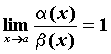, то бесконечно малые функциииназываютсяэквивалентными, обозначают~.

Вопрос 22      Определение. Функция     называется бесконечно малой функцией при, если.       Теорема. Функцияимеетпределв точкетогда и только тогда, когда в окрестности этой точки она может быть представлена в виде суммы числаи бесконечно малой функции. То есть

.

        Определение. Функция     называется бесконечно малой функцией более высокого порядка, чем бесконечно малая функция, если

.

        Определение. Функции     иназываются бесконечно малыми функциями одного порядка, если

.

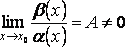        Определение. Функция     называется бесконечно малой функцией-го порядка относительно, если

.

        Определение. Бесконечно малые функции     иназываются эквивалентными бесконечно малыми функциями, если

.

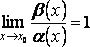Если функции     иявляются эквивалентными бесконечно малыми функциями, то записывают

.

При вычислении пределов бесконечно малые функции можно заменять на эквивалентные. Значение предела при этом не изменится. Основные эквивалентности при    

1.    

2.    

3.    

4.    

5.    

6.    

7.    

8.    

9.    

10.    

11.    

12.    

13.     .

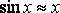
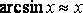
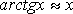
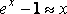
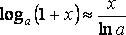
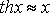
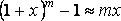        Из последней эквивалентности, следуют частные случаи.

1.    

2.    

3.    

4.    

5.    

6.     .

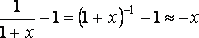
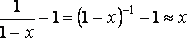
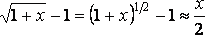
Вопрос 24

Первый замечательный предел

  Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере, при условии стремления этой дуги к нулю

.

  Непосредственное вычисление предела

приводит к неопределённости вида .    Изгеометрическихсоображений имеем S_OAС< S_OAC < S_OBC. Используя формулы площадей рассматриваемых фигур, получим

или

sin x<x< tgx

Разделив все части неравенства на sin x> 0, получим при условиих> 0

,

или

.

Так как функция у= cosxнепрерывна, то

.

Пользуясь теоремой о пределе промежуточной функции, получим окончательно

.

  Замечание. Если х< 0, то знаки неравенств изменяются на противоположные, выводы же остаются прежними.