2. Теорема Ролля.

Если функция f(x):

1. непрерывна на [a,b]

2. дифференцируема на (а,b)

3. принимает равные значения на концах отрезка: f(a)=f(b), то

найдется точка x₀ (a,b) такая что f `(x₀)=0.

По теореме Вейерштрасса что функция на [a,b] принимаем наибольшее M и наименьшее m значения.

1. если M=m, тогда это означает что функция не меняет своего значения на [a,b], а значит f `(x₀)=0;

2. если M<>m, тогда функция принимает минимум или максимум а значит по теореме Ферма в этих точках производная равна 0.

Мой способ.Если для любой точки х интервала (a,b) выполняется равенство f(х)=f(a)=f(b), то функция f является постоянной на этом интервале и поэтому для любой точки ξє (a,b) выполняется условие f’(ξ)=0.

Пусть существует точка х₀є (a,b), для которой f(х₀)≠ f(a), например, f(х₀)> f(a).Согласно теореме Вейерштрасса о достижимости непрерывной на отрезке функцией своих наибольшего и наименьшего значений, существует такая точка ξє[a,b], в которой f принимает наибольшее значение. Тогда f(ξ)≥ f(х₀)> f(a)=f(b).

Поэтому ξ≠a и ξ≠b,т.е. точка ξ принадлежит интервалу (a,b) и функция f принимает в ней наибольшее значение. Следовательно, согласно теореме Ферма выполняется равенство f’(ξ)=0.

Теорема лагранжа

Если функция f(x) непрерывна на [a,b], дифференцируема на (а,b), то найдется такая c(a,b), что:

Если g(x)=x, тогда f(x) и g(x) удовлетворяют условию т. Коши, а значи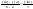т:

=>.Т

F(x)єС[a,b] существует F’(x) при хє(a,b)=>по Т Ролля

Существует с F’(c)=D

F’(c)=0=>f’(c)- =0=>f’(c)=

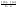
Геометрический смысл т. Лагранжа, что в точке c существует производная, график которой || хорде AB.

Если функция f непрерывна на отрезке [a,b] и в каждой точке интервала (a,b) имеет конечную или определенного знака бесконечную производную, то в этом интервале существует по крайней мере одна такая точка ξ, что f(b)- f(а)= f’(ξ)(b-a).

Доказательство. Рассмотрим вспомогательную функцию F(x)= f(x)-λх и определим число λ так, чтобы F(a)=F(b), т.е. чтобы f(а)-λа= f(b)-λb. Это равносильно тому, что .

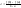Для функции F выполняются все условия теоремы Ролля. Действительно, функция f(x) непрерывна на отрезке [a,b], а функция λх, будучи линейной, непрерывна на всей числовой оси; поэтому и функция F(x)= f(x)- λх также непрерывна на отрезке [a,b]. Функция f имеет в каждой точке интервала (a,b) конечную или определенного знака бесконечную производную, а функция λх – конечную производную во всех точках числовой оси, поэтому их разность F(x) также имеет всюду в интервале (a,b) конечную или определенного знака бесконечную производную. Наконец, на концах отрезка [a,b], в силу выбора λ, функция F принимает одинаковые значения. Поэтому существует хотя бы одна такая точка ξ(a<ξ<b), что F’(ξ)=0. Из F(x)= f(x)-λх получаем F’(x)=f’’(x)-λ, поэтому f’’(ξ)-λ=0. Подставив сюда λ из , получимf’’(ξ).

. Доказать теорему Ферма.

Если функция дифференцируема в т. x₀ и т. x₀ является точкой локального экстремума, то f `(x₀)=0.

Предположим, что x₀ является локального точкой максимума в некоторой окрестности, тогда f(x)<f(x₀). По условию функция дифференцируема, следовательно .

1. ∆x > 0, тогда ≤0, предел справа не положителен

2. ∆x < 0, тогда ≥0, предел слева не отрицателен

А значит .

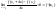Коши

Если функции g(x) и f(x) непрерывны на [a,b], дифференцируема на (а,b) и g`(x)≠0, то найдется такая

c(a,b), что:

Пусть g(b)≠g(a), т.к. если бы g(b)=g(a), то g(x) – удовлетворяла бы теореме Ролля, а значит g`(с)=0, что противоречит условию. Введем дополнительную функцию F(x)= f(x)-f(a)-λ (g(x)-g(a)), λ=(f(b) -f(a))/ (g(b) -g(a)). Данная функция удовлетворяет всем требованиям т. Ролля, т.к. F(a)=F(b). А значит существует точка c в которой F`(x)=0. А значит f `(c)-λ g`(c)=0 =>

. Доказать теорему Бернулли-Лапиталя для (0/0).

Если:

1. функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки a;

2. g`(x)<>0;

3. и ;

4. существует конечный или бесконечный предел:

Тогда справедливо:

.

Доопределим функции f(x) и g(x) в точке a: f(a) = g(a) = 0 и предположим, что x>a. Функции удовлетворят теореме Коши, а значит существует a<c<x:

При x→a, c→a, а значит из , т.е. существует конечный или бесконечный предел, а значит существует конечный или бесконечный предел

Аналогично доказывается и для x<a.