Вопрос 48! Дифференциалы высших порядков

      Будем рассматривать dxв выражении дляdyкак постоянный множитель.Тогда функцияdyпредставляет собой функцию только аргументаxи ее дифференциал в точкеxимеет вид (при рассмотрении дифференциала отdyбудем использовать новые обозначения для дифференциалов):

δ (d y) = δ [f' (x)d x] = [f' (x)d x] ' δ x=f'' (x)d(x) δx.

Дифференциал δ (d y) от дифференциалаdyв точкеx, взятый при δx = dx, называется дифференциалом второго порядка функцииf(x) в точкеxи обозначаетсяd²y, т.е.

d²y=f''(x)·(dx)².

В свою очередь, дифференциал δ(d²y)  от дифференциалаd²y, взятый при δx = dx, называется дифференциалом третьего порядка функцииf(x) и обозначаетсяd³yи т.д. Дифференциал δ(d^n-1y) от дифференциалаd^n-1f, взятый при δx=dx, называется дифференциаломn- го порядка (илиn- м дифференциалом) функцииf(x) и обозначаетсяdⁿy.    Докажем, что дляn- го дифференциала функции справедлива формула

dⁿy = y⁽ⁿ⁾·(dx)ⁿ,n= 1, 2, … (3.1)

   При доказательстве воспользуемся методом математической индукции. Для n= 1 иn= 2 формула (3.1) доказана. Пусть она верна для дифференциалов порядкаn- 1

dⁿ⁻¹y= y⁽ⁿ⁻¹⁾·(dx)ⁿ⁻¹,

и функция y^(n-1)(x) дифференцируема в некоторой точкеx. Тогда

Полагая δx = dx, получаем

что и требовалось доказать.    Для любого nсправедливо равенство

или

т.е. n- я производная функцииy =f(x ) в точкеxравна отношениюn- го дифференциала этой функции в точкеxкn- й степени дифференциала аргумента.

Вопрос 50! Формула Тейлора с остаточным членом в форме Лагранжа. Обобщенная теорема Ролля.

   Формула Тейлора.Пусть на интервале [a, b] функция f(x) дифференцируема n раз и выполняются следующие равенства:

f(a) = f(b) = f '(a) = f ''(a)= ... = f ^(n-1)(a)=0

Тогда внутри интервала [a, b] найдется хотя бы одно значение с, при котором

f ⁽ⁿ⁾(c) = 0

   Доказательство.Потеореме Ролляимеем

f '(x₀ ) = 0,

где a < x₀ < b. Тогдаf '(x)на интервале [a, x₀] удовлетворяет теореме Ролля, так как, по условию,f '(a) = 0иf '(x₀ ) = 0, а потому

f ''(x₁ ) = 0,

где a < x₁ < x₀.    Применяя теорему Ролля последовательно к функциямf ''(x), f '''(x), ..., f ^(n-1)(x), найдем наконец:

f ⁽ⁿ⁾(с) = 0,

где a < c < x_n-1 < b . Теорема доказана.    Выведем теперьформулу Тейлора с остаточным членом в форме Лагранжа.    Пусть функцияf (x)дифференцируемаnраз на интервале [a, b].    Рассмотрим вспомогательную функцию

(x) = f (x) - P (x),

где

   Продифференцируем nраз функцию(x). Тогда будем иметь

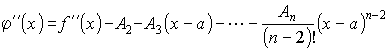. . . . . . . . . . . . . . . . . . . . . . . . . . . . ^(n-1)(x) = f^(n-1)(x) - A_n-1 - A_n(x - a), ⁽ⁿ⁾(x) = f⁽ⁿ⁾(x) - A_n

   Потребуем, чтобы функция (x)удовлетворяла условиям обобщенной теоремы Ролля. Тогда будем иметь

(1).

   Так как функция (x)удовлетворяет условиям обобщенной теоремы Ролля, то найдется такое значениес (a < c < b), что

⁽ⁿ⁾(с) = f⁽ⁿ⁾(с) - A_n = 0(2)

   Далее найдем из nпервых уравнений системы(1)коэффициентыA₀ , A₁ , ..., A_n-1:

A₀ = f(a), A₁ = f'(a), A₂ = f''(a), ..., A_n-1 = f^(n-1)(a),

а из уравнения (2) коэффициент A_n:A_n = f⁽ⁿ⁾(c)и подставим их значения в последнее уравнение системы(1):

,

где 0 <  < 1Заменяяbнаx, получим формулу Тейлора:

где 0 <  < 1Последнее слагаемое

называется остаточным членом в форме Лагранжа.    Приa = 0получается так называемаяформула Маклорена:

где 0 <  < 1, а остаточный член записывается в виде