Записка
.docxМетод конечных элементов (МКЭ) является эффективным численным методом решения задач механики сплошной среды, а также некоторых других типов задач, описываемых дифференциальными уравнениями в частных производных. Возникновение МКЭ (1950-е годы) было связано с решением задач строительной механики и теории упругости для космических исследований. Важным этапом явилось доказательство в 1963 г. связи МКЭ с методом Рэлея-Ритца, после чего МКЭ был распространен также на решение задач в других областях. В задачах строительной механики применение метода конечных элементов эквивалентно минимизации функционала полной потенциальной энергии системы на совокупности кусочно-заданных функций и позволяет свести задачу к системе линейных уравнений равновесия. В задачах динамики МКЭ позволяет: 1) моделировать движение системы прямым интегрированием определяющих уравнений динамического равновесия; 2) определять спектр собственных частот и форм колебаний модели. Подготовительным этапом в решении задачи при помощи МКЭ является создание сетки: разбиение объема исследуемого объекта (область определения задачи) на неперекрывающиеся подобласти – конечные элементы. Современные методы построения КЭ сеток позволяют создавать модели изделий с практически произвольной пространственной формой.
При выполнении расчетов на прочность методом конечных элементов (МКЭ) конструкций имеющих сложную структуру, большие размеры и требующих подробного разбиения, нередко расчетчик сталкивается с тем обстоятельством, что модель велика настолько, что не может быть решена на персональном компьютере по причине нехватки оперативной памяти. В этом случае рациональным является применение метода суперэлементов (подконструкций). В методе суперэлементов расчетная схема строится не сразу для всей конструкции, как в обычном МКЭ, а в несколько этапов - уровней, причем описание конечного элемента (КЭ) выполняется на самом нижнем уровне. Полная конструкция представляется в виде совокупности соподчиненных подконструкций различных уровней. Повторяющиеся части конструкции представляются типовым описанием и в процессе расчета могут использоваться неоднократно. Такая схема расчета является поэтапной и позволяет существенно сократить единовременные требования к оперативной памяти ЭВМ. Однако, в этом случае приходится выполнять ряд дополнительных вычислительных операций, не присущих МКЭ. Существует необходимость проанализировать структуру вычислительных затрат данного метода и разработать алгоритмы, позволяющие снизить время выполнения наиболее длительных стадий решения.
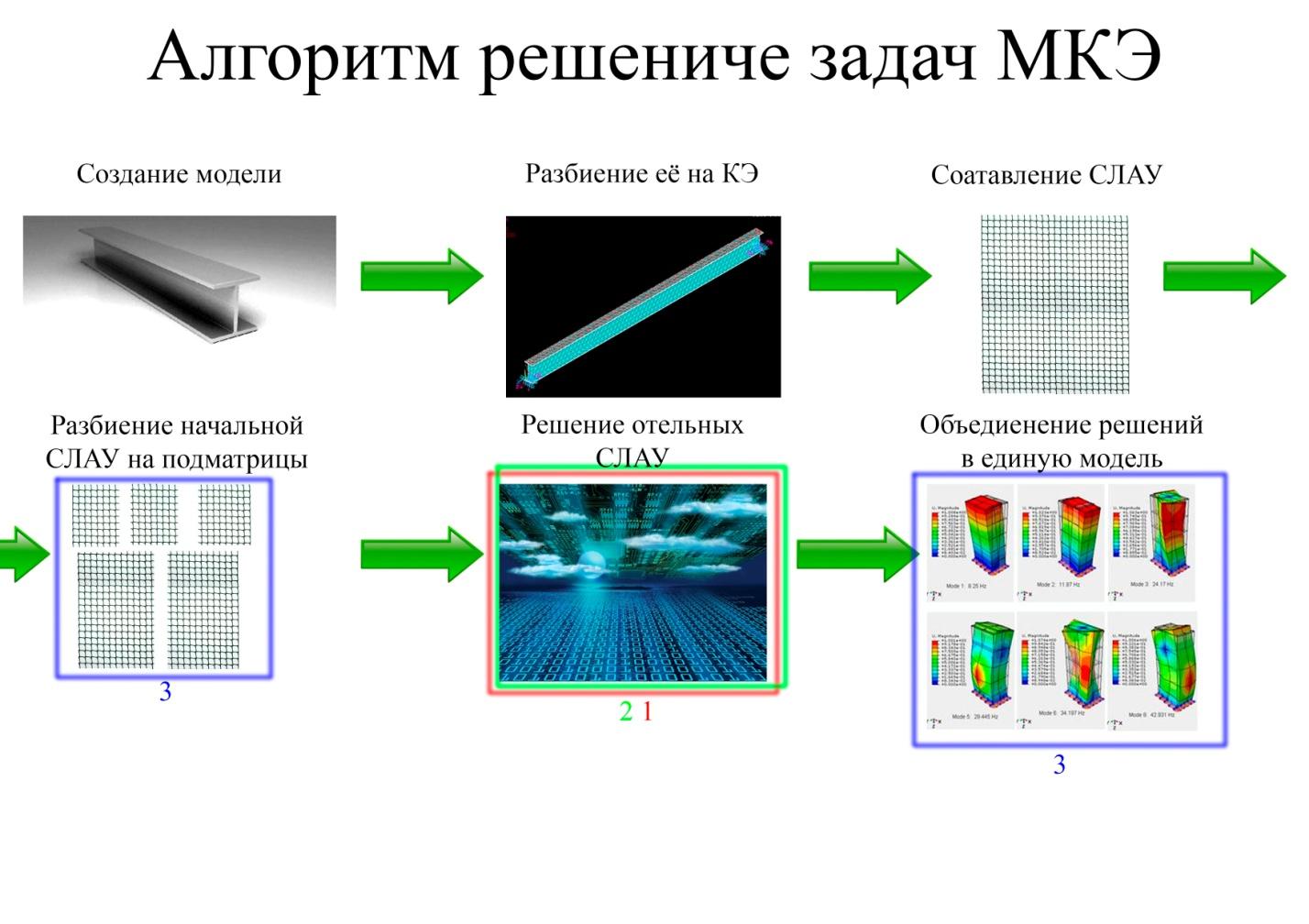
Решение задачи линейной упругой статики при помощи метода конечных элементов заключается в определении перемещений узлов сетки конечных элементов под действием внешних узловых сил. Линейность проявляется в том, что увеличение перемещений происходит прямо пропорционально увеличению нагрузки. Для определения искомых перемещений используют разрешающую СЛАУ МКЭ (0):
 (0)
(0)
где 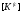 - матрица жесткости полной конечно-элементной
модели, составляется из матриц жесткости
отедльных конечных элементов;
- матрица жесткости полной конечно-элементной
модели, составляется из матриц жесткости
отедльных конечных элементов;
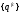 -
вектор узловых перемещений полной
конечно-элементной модели;
-
вектор узловых перемещений полной
конечно-элементной модели;
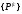 -
вектор узловых сил (нагрузок) полной
конечно-элементной модели;
-
вектор узловых сил (нагрузок) полной
конечно-элементной модели;
С
физической точки зрения уравнения
системы (0) представляют собой уравнения
равновесия узлов конечно-элементной
модели под действием внешниз нагрузок
и внутренних сил реакций со стороны
соседних узлов. Вектор узловых перемещений,
полученный в результате решения СЛАУ
(0), соответствует равновесному состоянию
(статическое равновесие) конечно-элементной
модели. Такое решение является единственным
и соответствует минимуму полной
потенциальной энергии системы.
Произведение
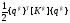 пердставляет собой потениальную энергию
упругих деформаций конечно-элементной
модели, следовательно матрица жесткости
является квадратичной формой и поэтому
обладает свойствами положительной
определенности, симметричности и
диагонального преобладания. В силу
топологии конечно-элементной сетки
матрица является существенно разреженной
(заполнение ненулевыми элементами менее
1 %). Исходя из перечисленных свойств
матрицы
пердставляет собой потениальную энергию
упругих деформаций конечно-элементной
модели, следовательно матрица жесткости
является квадратичной формой и поэтому
обладает свойствами положительной
определенности, симметричности и
диагонального преобладания. В силу
топологии конечно-элементной сетки
матрица является существенно разреженной
(заполнение ненулевыми элементами менее
1 %). Исходя из перечисленных свойств
матрицы
 выбирают методы решения СЛАУ (0). Как
упоминалось выше, существенные трудности
при решении СЛАУ (0) могут возникать при
увеличении размерности задачи –
количества уравнений системы. В этом
случае эффективным явлется применение
метода суперэлементов (МСЭ).
выбирают методы решения СЛАУ (0). Как
упоминалось выше, существенные трудности
при решении СЛАУ (0) могут возникать при
увеличении размерности задачи –
количества уравнений системы. В этом
случае эффективным явлется применение
метода суперэлементов (МСЭ).
Ключевым моментом МСЭ является возможность на каждом уровне декомпозиции рассматривать конструкцию, как состоящую из суперэлементов (объединений конечных элементов или суперэлементов более низкого уровня), взаимодействующих между собой только в граничных узлах. Это подразумевает необходимость описания поведения подструктуры через параметры только в граничных узлах.
Равновесие подструктуры (суперэлемента определенного уровня), как самостоятельной единицы, описывается через узловые параметры системой вида:
 (1)
(1)
где: - номер уровня поэтапного разбиения исходной конструкции;
- порядковый номер подструктуры (СЭ) для рассматриваемого уровня разбиения;
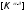 -
матрица жесткости подструктуры (СЭ);
-
матрица жесткости подструктуры (СЭ);
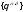 -
вектор узловых перемещений;
-
вектор узловых перемещений;
 -
вектор узловых усилий.
-
вектор узловых усилий.
Размерность системы (1) существенно меньше размерности полной системы (0) и зависит от количества суперэлементов (и уровней суперэлементов) на которые разделена исходная модель. Разделяя узловые параметры (узлы) суперэлемента на внутренние и внешние, запишем уравнение равновесия суперэлемента в блочном виде:
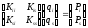 (2)
(2)
где:
 - индекс внутренних узловых параметров;
- индекс внутренних узловых параметров;

 -
индекс граничных узловых параметров;
-
индекс граничных узловых параметров;
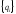 -
вектор перемещений внутренних узлов;
-
вектор перемещений внутренних узлов;
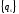 -
вектор перемещений граничных узлов;
-
вектор перемещений граничных узлов;
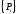 -
вектор нагрузок, приложенных к внутренним
узлам;
-
вектор нагрузок, приложенных к внутренним
узлам;
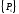 -
вектор нагрузок, приложенных к граничным
узлам;
-
вектор нагрузок, приложенных к граничным
узлам;
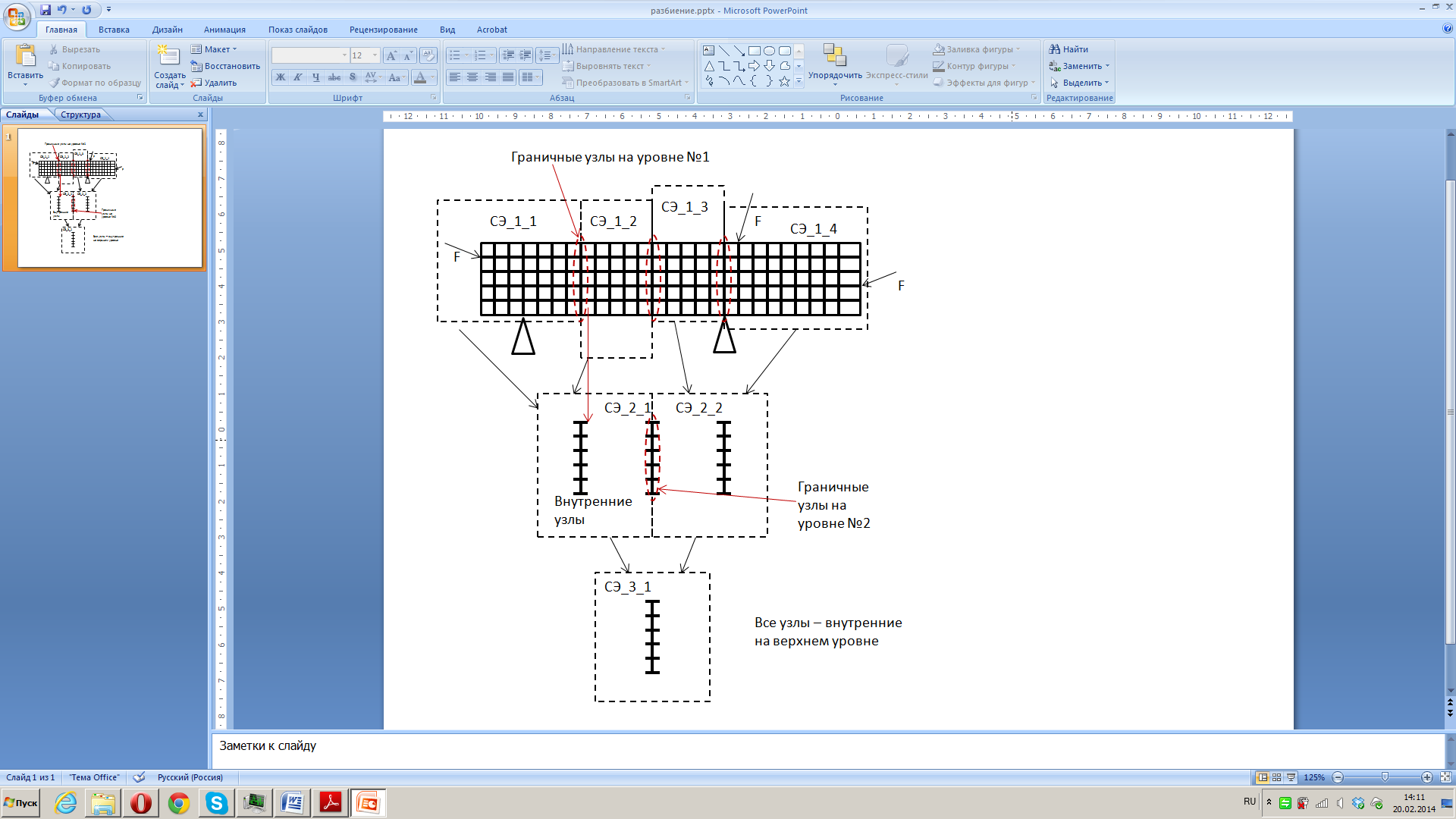
Матрица
жесткости суперэлемента
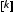 для работы с ним на более высоких уровнях
(описания взаимодействия суперэлементов
между собой) и вектор узловых усилий
для работы с ним на более высоких уровнях
(описания взаимодействия суперэлементов
между собой) и вектор узловых усилий
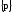 СЭ могут быть найдены по соотношениям
(3,4). После решения задачи на самом верхнем
уровне (фактически, после решения СЛАУ,
аналогичной (1), но без разделения на
блоки) требуется определить перемещения
внутренних узлов суперэлементов через
перемещения их граничных узлов, проходя
по структуре уровней сверху вниз и
используя соотношение (5)
СЭ могут быть найдены по соотношениям
(3,4). После решения задачи на самом верхнем
уровне (фактически, после решения СЛАУ,
аналогичной (1), но без разделения на
блоки) требуется определить перемещения
внутренних узлов суперэлементов через
перемещения их граничных узлов, проходя
по структуре уровней сверху вниз и
используя соотношение (5)
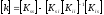 (3)
(3)
 (4)
(4)
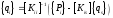 (5)
(5)
Таким образом, суперэлемент определяет поведение подструктуры через параметры в граничных узлах.
В соответствии с соотношением (3) для каждого суперэлемента в ходе суперэлементного алгоритма требуется находить следующее матричное произведение:
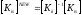 (6)
(6)
Важно
отметить, что
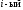 столбец матрицы
столбец матрицы
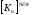 является
результатом решения системы линейных
алгебраических уравнений (СЛАУ) с
матрицей
является
результатом решения системы линейных
алгебраических уравнений (СЛАУ) с
матрицей
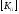 и правой частью в виде
и правой частью в виде
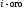 столбца матрицы
столбца матрицы
 .
Для отыскания подобных решений (т.е., в
конечном итоге матрицы
.
Для отыскания подобных решений (т.е., в
конечном итоге матрицы
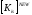 )
выгодно воспользоваться методом
Холецкого. При этом прямой ход, т.е.
нахождение такой верхней треугольной
матрицы
)
выгодно воспользоваться методом
Холецкого. При этом прямой ход, т.е.
нахождение такой верхней треугольной
матрицы
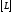 ,
что
,
что
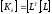 ,
выполняется однократно. Обратный ход
(подстановка правой части) выполняется
многократно, по количеству S
столбцов матрицы
,
выполняется однократно. Обратный ход
(подстановка правой части) выполняется
многократно, по количеству S
столбцов матрицы
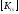 ,
т.е. столько раз, сколько степеней свободы
имеет суперэлемент в граничных узлах.
,
т.е. столько раз, сколько степеней свободы
имеет суперэлемент в граничных узлах.
Таким образом, можно выделить следующие основные вычислительные этапы метода суперэлементов:
1)
Составление
матриц жесткости суперэлементов
(соотношение 3).
Данный этап осуществляется однократно.
В дальнейшем полученные матрицы
суперэлементов могут использоваться
многократно в случае необходимости
решения задачи с различными векторами
нагрузки
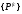 .
Основные вычислительные затраты на
данном этапе приходятся на следующие
операции:
.
Основные вычислительные затраты на
данном этапе приходятся на следующие
операции:
1.1)
разложение
матрицы
 к виду
к виду
 по алгоритму Холецкого
по алгоритму Холецкого
1.2)
Множественное решение СЛАУ с матрицей
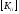 для определения матрицы
для определения матрицы
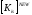 в соответствии с выражением (6)
в соответствии с выражением (6)
2)
Прямой
ход.
Вычисление векторов узловых сил для
граничных узлов суперэлементов по
соотношению (4). Выражение (4) сожержит в
своем составе решение СЛАУ с матрицей
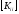 и правыми частями, содержащимися в
и правыми частями, содержащимися в
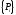 .На данном этапе необходимо пройти по
структуре уровней суперэлементов снизу
вверх. При этом для каждого суперэлемента
перед реализацией вычислений по выражению
(4) необходимо считать с жесткого диска
в оперативную память компьютера
разложение матрицы
.На данном этапе необходимо пройти по
структуре уровней суперэлементов снизу
вверх. При этом для каждого суперэлемента
перед реализацией вычислений по выражению
(4) необходимо считать с жесткого диска
в оперативную память компьютера
разложение матрицы
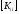 полученное на первом этапе (п. 1.1) и
имеющее существенный объем. Также
требуется считывать матрицу
полученное на первом этапе (п. 1.1) и
имеющее существенный объем. Также
требуется считывать матрицу
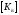 до преобразования (6), занимающую
существенно меньший объем памяти,
поскольку для нее хранятся только
ненулевые элементы.
до преобразования (6), занимающую
существенно меньший объем памяти,
поскольку для нее хранятся только
ненулевые элементы.
В результате выполнения прямого хода удается вычислить вектор узловых сил, действующий на верхнем уровне суперэлементов. При этом система уравнений равновесия для верхнего уровня (фактически на этом уровне формируется «последний и единственный» суперэлемент) аналогична (0), но имеет существенно меньшую размерность, удовлетворяющую имеющемуся объему оперативной памяти. На верхнем уровне решение полученной СЛАУ, аналогичной (0) производится с найденным в процессе прямого хода вектором узловых сил верхнего уровня. В результате определяются перемещения узлов модели, оставшихся на верхнем уровне. Эти узлы являются граничными для суперэлементов в предыдущем (более низком) уровне.
3)
Обратный
ход.
После определения перемещений на верхнем
уровне становятся известными перемещения
граничных узлов суперэлементов более
низкого уровня
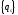 .Далее требуется воспользоваться
выражением (5) для определения перемещений
внутренних узлов суперэлементов данного
уровня. Внутренние узлы в данном случае
также являются внешними для суерэлементов
следующего более низкого уровня. Таким
образом обратный ход характеризуется
движением по структуре уровней
сверху-вниз. Так же как и в случае прямого
хода требуется считывать разложение
матрицы
.Далее требуется воспользоваться
выражением (5) для определения перемещений
внутренних узлов суперэлементов данного
уровня. Внутренние узлы в данном случае
также являются внешними для суерэлементов
следующего более низкого уровня. Таким
образом обратный ход характеризуется
движением по структуре уровней
сверху-вниз. Так же как и в случае прямого
хода требуется считывать разложение
матрицы
 и матрицу
и матрицу
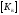 для каждого суперэлемента.
для каждого суперэлемента.
Первый этап МСЭ характеризуется большими вычислительными затратами, но проводится однократно. Второй и третий этапы характеризуются существенно меньшими вычислительными затратами, но требуют большого объема работы с дисковой памятью (медленная операция). Кроме того, второй и третий этапы часто требуется осуществлять многократно.
Решение задачи в случае наличия физической нелинейности (например, пластического деформирования отдельных зон конструкции) требует множества последовательных итераций, на каждой из которых осуществляется однократное упругое решение задачи со специальным образом модифицированным вектором узловых сил. Итерационное решение также требуется при решении контактных задач (геометрическая нелинейность), некоторых типов задач динамики (определение собственных частот и форм колебаний) и в ряде других случаев. При этом, матрицы подконструкций (см. выражение 3) составляются однократно, а определение сокращенных векторов сил (4) и перемещений (5) конструкции производится многократно.
Таким образом, с вычислительной точки зрения в процессе решения задачи требуется:
1) С одной стороны
требуется осуществлять решение СЛАУ с
матрицей
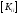 на этапе (6) составления матриц
подконструкций. В этом случае количество
правых частей весьма велико, обычно 100
– 5000, при количестве строк в матрице
на этапе (6) составления матриц
подконструкций. В этом случае количество
правых частей весьма велико, обычно 100
– 5000, при количестве строк в матрице
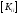 10000 – 150000. Матрица
10000 – 150000. Матрица
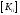 имеет разреженную структуру. В этом
случае считается целесообразным
использовать прямой метод решения СЛАУ
(например, методом Холецкого), несмотря
на большой объем вычислительных затрат
и оперативной памяти, поскольку
«подстановка» правой части (столбцы
матрицы
имеет разреженную структуру. В этом
случае считается целесообразным
использовать прямой метод решения СЛАУ
(например, методом Холецкого), несмотря
на большой объем вычислительных затрат
и оперативной памяти, поскольку
«подстановка» правой части (столбцы
матрицы
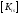 )
выполняется относительно быстро и не
требует итераций.
)
выполняется относительно быстро и не
требует итераций.
2) С другой стороны,
требуется определять вектор перемещения
узлов модели многократно (при действии
различных векторов узловых сил) с уже
составленными на первом этапе матрицами
подконструкций. Поэтому возникает
необходимость многократного
последовательного решения СЛАУ в
выражении (4) относительно векторов сил
суперэлементов
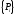 .
(аналогичная процедура затем применяется
и для определения перемещений внутренних
узлов подконструкций (5)). В случае решения
задачи о пластическом деформировании
в
.
(аналогичная процедура затем применяется
и для определения перемещений внутренних
узлов подконструкций (5)). В случае решения
задачи о пластическом деформировании
в
 содержится 1 столбец. Если осуществляется
итерационный поиск собственных частот
и форм колебаний, то в
содержится 1 столбец. Если осуществляется
итерационный поиск собственных частот
и форм колебаний, то в
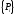 содержится от 10 до 50 столбцов. На данном
этапе для вычисления выражения (4,5)
требуется считать с диска сохраненное
на первом этапе разложение матрицы
содержится от 10 до 50 столбцов. На данном
этапе для вычисления выражения (4,5)
требуется считать с диска сохраненное
на первом этапе разложение матрицы
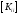 в случае использования прямого метода
(метода Холецкого). Матрица
в случае использования прямого метода
(метода Холецкого). Матрица
 после разложения претерпевает существенное
заполнение (количество ненулевых
элементов многократно увеличивается
в 10 и более раз), поэтому типовой объем
данных этой матрицы 0,5-10 Гб. Считывание
такого объема данных с жесткого диска
на каждой итерации для каждого
суперэлемента (в соответствие с
блок-схемой) занимает существенное
количество времени и лимитирует
производительность программы (процессор
в этом случае загружен слабо). Поэтому
на данном этапе предлагается применить
итерационный метод решения СЛАУ – метод
сопряженных градиентов с предобуславливанием.
Скорость сходимости данного метода
критическим образом зависит от числа
обусловленности матрицы, поэтому
применяют методы предобуславливания
[4], которые с одной стороны увеличивают
скорость сходимости метода сопряженных
градиентов и с другой стороны не приводят
к существенному заполнению исходной
матрицы (чтобы не увеличивать слишком
сильно объем оперативной и дисковой
памяти). Для предобуславливания используют
так называемое неполное разложение
Холецкого, суть которого заключается
в том, что при проведении процедуры
Холецкого сохраняют только те новые
ненулевые элементы матрицы, которые в
наибольшей степени повысят скорость
сходимости итерационного процесса. При
этом пользователь определяет допустимый
объем заполнения матрицы по сравнению
с исходным объемом.
после разложения претерпевает существенное
заполнение (количество ненулевых
элементов многократно увеличивается
в 10 и более раз), поэтому типовой объем
данных этой матрицы 0,5-10 Гб. Считывание
такого объема данных с жесткого диска
на каждой итерации для каждого
суперэлемента (в соответствие с
блок-схемой) занимает существенное
количество времени и лимитирует
производительность программы (процессор
в этом случае загружен слабо). Поэтому
на данном этапе предлагается применить
итерационный метод решения СЛАУ – метод
сопряженных градиентов с предобуславливанием.
Скорость сходимости данного метода
критическим образом зависит от числа
обусловленности матрицы, поэтому
применяют методы предобуславливания
[4], которые с одной стороны увеличивают
скорость сходимости метода сопряженных
градиентов и с другой стороны не приводят
к существенному заполнению исходной
матрицы (чтобы не увеличивать слишком
сильно объем оперативной и дисковой
памяти). Для предобуславливания используют
так называемое неполное разложение
Холецкого, суть которого заключается
в том, что при проведении процедуры
Холецкого сохраняют только те новые
ненулевые элементы матрицы, которые в
наибольшей степени повысят скорость
сходимости итерационного процесса. При
этом пользователь определяет допустимый
объем заполнения матрицы по сравнению
с исходным объемом.
В связи с описанной общей структурой решения предлагается опробовать новый подход к организации вычислений при реализации метода суперэлементов.
Предлагается этап
(1) оставить без изменений (составление
матриц), а на этапах 2 и 3 для расчета
предобуславливателя использовать уже
найденное на первом этапе разложение
Холецкого, по которому может быть
составлен качествнный предобуславливатель,
избегая таким образом с одной стороны
дополнительных вычислительных затрат,
с другой стороны существенно сокращая
объем дисковой памяти для сохранения
предобуславливателя
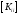 вместо полного разложения этой матрицы.
Далее на втором этапе решение СЛАУ с
правыми частями
вместо полного разложения этой матрицы.
Далее на втором этапе решение СЛАУ с
правыми частями
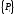 осуществляется при помощи итерационного
метода сопряженных градиентов. Таким
образом, существенно сокращается
требуемое количество оперативной памяти
и время, требуемое на считывание с диска
необходимых матриц.
осуществляется при помощи итерационного
метода сопряженных градиентов. Таким
образом, существенно сокращается
требуемое количество оперативной памяти
и время, требуемое на считывание с диска
необходимых матриц.
На основе выше изложенного предлагается сформулировать 3 взаимосвязанных блока задач на курсовой проект:
Задание №1 (3 человека)
- разработка
программы для решения системы (6) прямым
методом (метод Холецкого или LDLT
– разложение) [3, стр. 705]. Матрица
 хранится в профильной форме;
хранится в профильной форме;
- разработка
программы для решения системы (4,5) (для
векторов сил и перемещений) на основе
метода сопряженных градиентов; Матрица
 хранится в разреженной форме – только
ненулевые элементы. [3, стр. 749]
хранится в разреженной форме – только
ненулевые элементы. [3, стр. 749]
- разработка
программы для расчета предобусловливателя
[4] матрицы
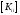 на основе метода Холецкого с использованием
ранее найденного полного разложения.
на основе метода Холецкого с использованием
ранее найденного полного разложения.
- проведение тестовых расчетов (матрицы предоставляет РК5 из собственных программ) для задач различной размерности. Требуется осуществить оценку времени решения и полученного выигрыша в производительности в зависимости от настроек алгоритма.
- анализ влияния объема предобуславливателя на время решения задачи в целом (сравнение производится по суммарному времени: считывание мтариц и решение СЛАУ). Сравнение различных стратегий предобуславливания.
Задание № 2 (3-4 человека)
Эффективность
решения СЛАУ (3,4,5,6) и степень ее заполнения
в процессе разложения Холецкого
существенно зависит от порядка нумерации
узлов (топологии сетки), как показано в
[1]. В зависимости от способа нумерации
объем памяти (и вычислений) для одной и
той же задачи может изменяться на 1
порядок для пространственных КЭ сеток.
Поэтому актуальной является задача
поиска оптимальной нумерации узлов с
целью минимизации ширины профиля (либо
минимизации заполнения) матрицы
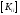 .
.
Методы решения данной задачи на основе теории графов представлены в [1]. Применяются различные способы в зависимости от способа хранения матрицы и метода последующего решения СЛАУ.
Предлагается:
- реализовать контейнер для хранения информации о графе СЛАУ и выполнения базовых операций над ним; [1, стр 21-54]
- реализовать обратный алгоритм Катхила-Макки для снижения ширины профиля матрицы в случае прямого решения СЛАУ. [1, стр 65]
- реализовать алгоритм минимальной степени для случая итерационного решения СЛАУ с учетом предобусловливания и разреженной схемы хранения; [1, стр 119]
- провести тестовые расчеты для КЭ сеток, предоставленных РК5. Оценить степень сокращения объема матриц в зависимости от настроек алгоритма.
полученные результаты могут применяться в качестве предварительного этапа для задания 1 с целью существенного ускорения решения.
Задание № 3 (3 человека)
Деление полной конечно-элементой сетки модели на суперэлементы (неперекрывающиеся односвязные совокупности конечных элементов полностью покрывающие исходную сетку) представляет собой сложную трудоемкую задачу в случае больших моделей, когда требуется обеспечить заданный характерный объем суперэлементов и одновременно снизить количество граничных узлов, от которых существенно зависит время решения задачи (количество столбцов в соотношении 6).
Предлагается реализовать деление КЭ сетки на суперэлементы при помощи теории графов с использованием метода многоуровневого деления графа из [2].
- реализовать алгоритм многоуровневого «огрубления» (сжатия) графа;
- реализовать алгоритм деления пополам графа, полученного на верхнем уровне сжатия, с условием минимального размера сечения графа;
- реализовать алгоритм распространения полученного деления графа на все уровни «огрубления» с постепенным выравниванием суперэлементов;
Осуществить анализ предлагаемых методов и обзор литературы по каждому блоку задачи.
- выполнить тестовые расчеты для КЭ сеток разной размерности, предоставленных РК5;
Полученные результаты в дальнейшем могут быть использованы совместно с результатами заданий № 1 и 2 для повышения эффективности задачи определения напряженно-деформированного состояния конструкций методом суперэлементов.
Литература:
1) А. Джордж, Дж. Лю, Численное решение больших разреженных систем уравнений, 1984, 333 с.
2) George Karypis, Vipin Kumar, Multilevel graph partitioning schemes + сайт лаборатории ParMETIS
3) Bathe K-J. Finite element procedures. New Jersey: Prentice Hall, 1996. 1037 p.
4) Benzi M. Preconditioning techniques for large linear systems: a survey, 2002, Journal of Computational Physic, N 182, pp. 418-477
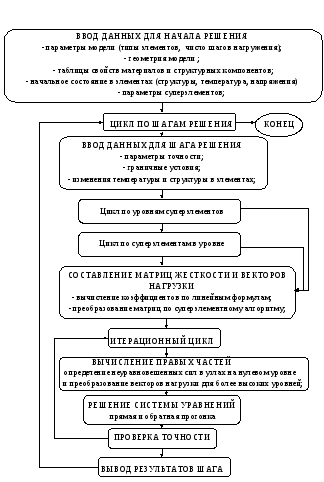
ПРИЛОЖЕНИЕ
Блок схема программы для расчета напряженно-деформированного состояния методом суперэлементов (с учетом физической нелинейности) представлена на рисунке :