
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
8.2 ] Спектральный метод решения задачи дифракции 571
суммы гармонических колебаний различных частот:
7 |
1 |
|
% D# |
|
(8.17) |
|
2 |
|
|||||
|
|
|
|
|||
Точно так же произвольное граничное поле 70 представ- |
||||||
ляется в виде интеграла |
|
|
|
|
|
|
70 |
1 |
|
%0 4 D7 |
, |
(8.18) |
|
|
|
|||||
2 |
||||||
|
|
|
|
|||
т. е. в виде непрерывной суммы плоских волн различных пространственных частот.
Ранее мы говорили о замечательном соотношении, связывающем длительность сигнала с шириной его спектра (соотношении неопределенностей (1.52)): 2$. Из математической тождественности выражений (8.17) и (8.18) следует, что аналогичное соотношение неопределенностей должно связывать протяженность граничного поля с шириной 4 его пространственного спектра:
4 2$ |
(8.19) |
Пространственная протяженность граничного поля, согласно граничным условиям Кирхгофа (8.2), определяется характерным размером препятствия, в нашем примере — размером отверстия в непрозрачном экране. Поэтому ширина спектра плоских волн (область значений пространственных частот 4, в которой пространственный спектр %0 4 заметно отличен от нуля) можно
оценить так:
4 2)
Разброс пространственных частот определяет разброс направлений слагаемых плоских волн за препятствием:
4 # ,
откуда # или, для малых углов,
# )
Это и есть дифракционная расходимость пучка света за отверстием размера .
Важно подчеркнуть, что речь идет о линейной задаче: распространение волны от плоскости 0 до плоскости наблюдения& 0 описывается линейным волновым уравнением (4.5) или, поскольку мы пользуемся комплексным представлением, линейным уравнением Гельмгольца (4.26). Основное свойство линейного уравнения: сумма решений является решением, или,

572 |
Дифракция |
[ Гл. 8 |
более подробно, если мы имеем два решения 71 , и 72 , , удовлетворяющих на границе 0 условиям
71 , 0 710 и 72 , 0 720
(710 и 720 — заданные функции координаты ), то линейная суперпозиция решений 71 , и 72 , :
7 , 171 , 272 ,
есть решение уравнения Гельмгольца, удовлетворяющее граничному условию:
70 1710 2720
Вспомним теперь, что плоская волна
7 , D 7 |
2 72 |
|
есть решение уравнения Гельмгольца, удовлетворяющее на плоскости 0 граничному условию
7 , 0 D7 ,
поэтому сумма плоских волн
7 , D 7 |
2 72 |
(8.20) |
|
есть решение, удовлетворяющее граничному условию (8.16). Это и есть решение дифракционной задачи. Мы нашли вол-
новое поле в любой плоскости наблюдения, отстоящей от препятствия (непрозрачного экрана с отверстием) на расстояние .
В более общем случае, если граничное поле 70 представляется непрерывной суперпозицией плоских волн (8.18), искомое решение имеет вид
7 , %0 4 D |
7 2 72 |
, |
(8.21) |
|
где %0 4 — преобразование Фурье граничного поля 70 (т. е.
спектр плоских волн граничного поля).
В выражениях (8.20) или (8.21) существенным является следующее обстоятельство: каждая слагаемая плоская волна при распространении до плоскости наблюдения & 0 приоб-
ретает свой фазовый набег 2 42 , зависящий от ее
пространственной частоты
4 . Поэтому фазовые соотношения между слагаемыми плоскими волнами на границе 0 и в плоскости наблюдения, отстоящей на расстоянии , различны. Изменение фазовых соотношений между слагаемыми плоскими волнами приводит к тому, что изменяется результат интерференции этих плоских волн. Поэтому результирующее поле 7 ,


574 |
Дифракция |
[ Гл. 8 |
В большинстве оптических дифракционных задач речь идет о препятствиях, размеры которых заметно превышают длину световой волны, поэтому пространственные частоты плоских волн, возникающих при дифракции на препятствиях размера , согласно (8.19), существенно меньше волнового числа 2$ :
2 |
2 |
|
|
|
|
|
|
) |
|
||
Используя условие 4 , получаем, разлагая радикал 2 42 в ряд по степеням малого параметра 4 2 и ограничиваясь двумя членами разложения,
|
|
|
|
|
2 |
|
2 42 |
4 |
(8.24) |
||||
|
2 |
|
||||
Тогда выражение для пространственной частотной характеристики свободного пространства G 4 принимает вид
G 4 D 2 42 ,
который используют обычно при решении дифракционных задач в оптике. В частности вместо формулы (8.21) получаем
7 , D %0 4 |
|
42 4 |
(8.25) |
|
2 |
|
|
Напомним еще раз, что функция 7 , описывает картину дифракции (комплексную амплитуду волны) в фиксированной плоскости наблюдения, находящейся на расстоянии за препятствием, а функция %0 4 — пространственный спектр (преобразование Фурье) светового поля 70 в плоскости, непосредственно примыкающей к препятствию (это поле находится с помощью граничных условий Кирхгофа (8.3)).
Все соотношения легко обобщаются на случай, когда световое поле во «входной плоскости» 0 является функцией двух переменных. Тогда вместо (8.16) имеем
70 , D 7 $ ,
где 4 , — пространственные частоты — проекции вектора !-й плоской волны на оси , : 4 , . В случае непрерывного спектра плоских волн вместо (8.18) получаем
70 , |
1 |
|
%0 4, D 7 $ |
, |
|
2 |
|||
4 |
|
|
|
|
где %0 4, — двумерное преобразование Фурье (пространственный спектр светового поля 70 , :
1
%0 4, 4 2 70 , D 7 $

8.2 ] Спектральный метод решения задачи дифракции 575
Решение дифракционной задачи (искомое световое поле в «выходной плоскости» & 0) принимает вид
7 , , D 7 $ |
2 72 $2 |
|
|
или, в случае непрерывного спектра, |
|
7 , , %0 4, D 7 $ 2 72 $2
Частотная характеристика свободного пространства является в общем случае также функцией двух переменных 4,
G 4, D 2 72 $2 ,
где 2 42 2 — -компонента вектора ! плоской волны с
пространственными частотами 4 , ( 2 2 2
2 2). Эта функция связывает между собой простран-
ственные спектры световых полей во «входной» и «выходной» плоскостях
% 4, , %0 4, D 2 72 $2
Проиллюстрируем спектральный метод, рассмотрев задачу дифракции плоской волны на амплитудной синусоидальной решетке. Итак, пусть плоская волна единичной амплитуды, бегущая вдоль оси , 7- 1 D падает на решетку с функцией пропускания (8.5) (решетка установлена в плоскости 0). Тогда на выходе из решетки в плоскости 0 , непосредственно примыкающей к ней, имеем, используя (8.3):
70 1
Представим это граничное поле в виде (8.16). В данном случае с помощью формулы Эйлера находим
70 1 2 D 2 D
Мы получили разложение (8.16): каждое слагаемое в граничном поле 70 «ответственно» за появление «своей» волны в области & 0. Первое слагаемое дает волну, бегущую вдоль оси : 71 , 1 D . (Действительно, 71 , есть решение уравнения Гельмгольца, удовлетворяющее граничному условию 71 , 0 1.) Аналогичным образом, два других слагаемых
ответственны за появление волн 72 , 2 D 2 2
и 73 , 2 D 2 2 , имеющих пространственные частоты и бегущих в направлениях # . Полагаем, что период решетки 2$ существенно больше длины

576 Дифракция [ Гл. 8
волны и, следовательно, пространственная частота много меньше .
Тогда, используя приближение (8.24), находим
7 , 1 D D D |
|
2 2 |
|
D D |
2 2 |
|
|
|
|
|
|||||
2 |
|
2 |
|
|
|
|
|
После простых преобразований окончательно получаем |
|
||||||
7 , D 1 C |
2 |
|
|||||
|
|
2 |
|
|
|
||
Последнюю формулу можно использовать для анализа картины дифракции, возникающей на различных расстояниях от ре-
шетки. |
|
2 2 |
|
На расстояниях , для |
которых |
2$ (т. е. |
|
4$ 2 2 2 ), |
имеем: |
D 2 2 |
1, поэто- |
му 7 , D 70 . Следовательно, с точностью до постоянного множителя D воспроизводится граничное световое поле. Воспроизводится, разумеется, наблюдаемая картина интенсивности: : , :0 . Найдем ее видность:
2 : : : : , полагая глубину модуляции малой и пренебрегая членами порядка 2. Тогда
: , 7 , 2 1 2 и 2 2
На расстояниях , для которых D 2 2 , т. е.2 2 $ 2 2$ , имеем
7 , 1
Картина интенсивности: : , 1 — с точностью до членов порядка 2 получаем равномерную (не зависящую от ) засветку плоскости наблюдения: 2 0. Таким образом, периодически по изменяется видность наблюдаемой дифракционной картины. Причина этих изменений, разумеется, в различии фазовых набегов трех плоских волн, бегущих в области & 0: осевой волны, бегущей вдоль оси , и двух боковых волн, бегущих
внаправлениях # .
8.3.Дифракция на периодических структурах
(эффект Талбота)
Рассмотрим теперь произвольную плоскую периодическую структуру. Такая структура может быть образована одинаковы-
ми объектами, расположенными на равных расстояниях друг от друга в плоскости 0, либо представлять собой экран с периодически расположенными отверстиями одинаковой формы. Пусть такая структура (будем называть ее решеткой) освещается слева

8.3 ] Дифракция на периодических структурах (эффект Талбота) 577
плоской нормально падающей волной. Тогда, согласно граничным условиям Кирхгофа (8.3), в плоскости 0 , примыкающей к структуре справа, возникает пространственно-периодическое с периодом световое поле 70 (рассматриваем для простоты функцию одной переменной), которое можно представить в виде ряда Фурье:
70 D |
2 |
(8.26) |
|
Каждое слагаемое ряда ответственно за появление плоской волны в области & 0, пространственная частота которой 4 2$ определяет направление волнового вектора ! (4 # ) этой волны, соответственно, # 4. Комплексная амплитуда волны в плоскости наблюдения, отстоящей на расстоянии от решетки, имеет вид (8.20).
Напомним, что величина 2 42 представляет собой набег фазы плоской волны, имеющей пространственную частоту 4 .
Будем полагать, что в сумме плоских волн (8.26), образующих периодическую структуру, существенно отличны от нуля лишь значения , для которых 4 2$ много меньше
! 2$ . В этом случае, используя приближение (8.24), получаем
|
|
42 |
(8.27) |
2 |
Или, поскольку 4 2$ , то 2 2$ 2 2. Конечно, существенную роль играет лишь разность фазовых набегов, поэтому будем сравнивать набег фазы -й плоской волны с набегом фазы 0 плоской волны, бегущей вдоль оси (перпендикулярной плоскости решетки): 0 . Мы получаем
|
|
2 2 |
2 2 |
(8.28) |
|||
0 |
|
|
|
|
|||
2 |
2 |
||||||
Рассмотрим плоскость наблюдения, отстоящую от решетки на |
|||||||
расстояние |
2 2 |
|
|
|
|
||
1 |
|
|
|
(8.29) |
|||
|
|
|
|||||
|
|
|
|
|
|
||
В этой плоскости имеем 2$ 2, т. е. относительный набег фазы всех плоских волн кратен величине 2$. Очевидно, что и разность фазовых набегов любых двух волн (с простран-
ственными частотами 1 2$ и 2 2$ ), равная 2$ 2 2 ,
1 2
также кратна 2$. Но изменение разности фаз колебаний на величину, кратную 2$, ничего не меняет в суммарном колебании. Мы пришли к замечательному результату: фазовые соотношения между слагаемыми плоскими волнами оказались одинаковыми как в плоскости, примыкающей к решетке (где сумма плоских
19 Основы физики. Т. I

578 |
Дифракция |
[ Гл. 8 |
волн (8.26) образовала граничное периодическое поле 70 ), так и в плоскости (8.29). Одинаковость (с точностью до величины, кратной 2$) фазовых соотношений слагаемых плоских волн приводит к тому, что одинаков и результат интерференции этих плоских волн, т. е. световое поле в плоскости 1 2 2 отличается от граничного поля 70 лишь постоянным фазовым множителем D :
7 , 1 D 1 70
Мы наблюдаем в плоскости 1 периодическую структуру, тождественно повторяющую граничное поле 70 . Очевидно также, что такое восстановление (воспроизведение) изображения периодической структуры повторяется на расстояниях, крат-
ных 1: |
|
|
2 2 |
1, 2, |
(8.30) |
Описанный эффект называют эффектом самовоспроизведе-
ния, или по имени первооткрывателя У. Талбота (1800–1877)
эффектом Талбота.
Заметим, что периодически по воспроизведение граничной периодической структуры происходит в области френелевской дифракции 82 2 2 . Реально любая структура имеет конечные размеры (содержит конечное число периодов ), что не учитывалось нами при изучении эффекта. Рано или поздно с ростом конечные размеры решетки начинают приводить к ухудшению эффекта самовоспроизведения.
8.4. Область геометрической оптики
Опыт показывает, что в некоторых случаях (когда плоскость наблюдения отстоит недалеко от препятствия или когда размеры препятствия достаточно велики) наблюдаемая картина оказыва-
ется подобной картине поля на границе — ситуация, показанная на рис. 8.1 а: наблюдаемая картина получается геометрическим проецированием отверстия на плоскость наблюдения. Итак, вы-
ясним условия, когда выводы, основанные на представлениях геометрической оптики, справедливы.
Пусть щель в непрозрачном экране ширины освещается плоской нормально падающей волной. Тогда граничное поле 70 имеет вид, показанный на рис. 8.9 а. Его пространственный спектр %0 4 (фурье-преобразование функции 70 ) показан на рис. 8.9 б; он имеет точно такой же вид, что и спектр прямоу-
гольного импульса, который мы изучали в гл. 1.4.
Функция %0 4 заметно отлична от нуля в пределах главного максимума, в области 4 ' 2$ . Поскольку мы полагаем, что

580 |
|
|
Дифракция |
|
|
|
|
[ Гл. 8 |
|
|
8.5. Дифракция Фраунгофера |
|
|
|
|
||||
Используем общее соотношение (8.21) для изучения ди- |
|||||||||
фракционной |
картины |
на |
большом |
удалении от препятствия, |
|||||
в области значений волнового параметра 8 1 (об- |
|||||||||
ласть дифракции Фраунгофера (по имени немецкого физика |
|||||||||
Й. Фраунгофера (1787–1826)). Для оценки интеграла (8.21) вос- |
|||||||||
пользуемся методом, называемым методом стационарной фа- |
|||||||||
зы. Показатель экспоненты в (8.21), имеющий вид |
|
|
|
|
|||||
|
4 2 42 4, |
|
|
(8.33) |
|||||
разложим в ряд Тейлора в окрестности некоторой точки 4 40: |
|||||||||
|
|
|
1 |
|
2 |
|
|
|
|
4 40 40 4 40 2 40 4 40 |
|
|
|
|
|||||
|
|
|
1 |
|
3 |
(8.34) |
|||
|
|
|
6 40 4 40 |
|
|
||||
Выберем точку 40 так, чтобы |
|
|
|
|
|
|
|||
|
|
|
40 0 |
|
|
|
|
|
|
Используя (8.33), находим 4 |
и, приравнивая |
||||||||
|
|
|
|
2 2 |
|
|
|
|
|
производную 4 нулю, получаем |
|
|
|
|
|
|
|||
|
4 40 |
, |
|
|
(8.35) |
||||
|
|
|
2 2 |
|
# |
|
|
|
|
где 2 2 — расстояние от начала координат граничной |
|||||||||
плоскости 0 до точки наблюдения , . Значение 40 явля- |
|||||||||
x |
x |
|
ется точкой |
экстремума |
функции |
||||
|
4 . Ее |
называют стационарной |
|||||||
|
x |
|
|||||||
|
|
точкой: в ее окрестности фаза 4 |
|||||||
k0 |
r |
|
|||||||
|
изменяется наиболее медленно. |
|
|||||||
|
|
|
|
||||||
O |
z |
z |
Из всего спектра плоских волн, |
||||||
|
|||||||||
|
|
бегущих |
от |
границы |
|
0 |
в |
||
|
|
|
|||||||
|
|
|
области & 0, стационарная точ- |
||||||
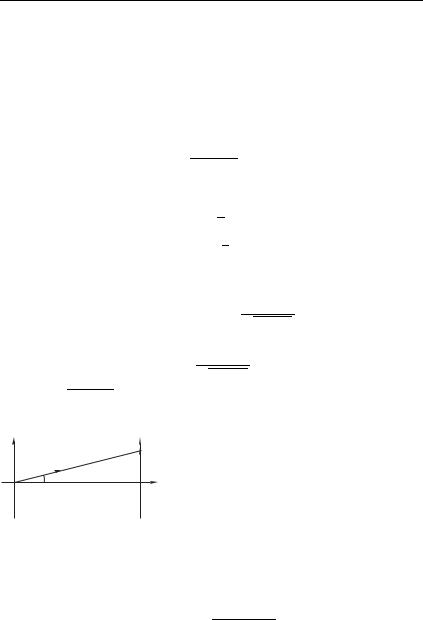
Рис. 8.10 |
|
ка 40 выделяет плоскую волну с |
|||||||
|
волновым |
вектором ! |
(рис. 8.10): |
||||||
|
|
|
|||||||
40 0 0 #, где # — направление на точку наблюдения |
|||||||||
( # ). |
|
|
|
|
|
|
|
|
|
Дважды дифференцируя функцию (8.33), найдем 4 : |
|
||||||||
4 2
2 2 3 2
Используя далее значение 40, имеем
40 , 40 |
# |
3 |
|
(8.36) |
|
|
|
|
|||
|
2 |
||||


 L
L  f
f