
3870
.pdf
Выпуск № 1 (45), 2017 |
ISSN 2541-7592 |
Для изучения воздействий от движения зрителей за рубежом проводились многочисленные экспериментальные и теоретические исследования [13, 14, 16—21], в ходе которых была получена аппроксимация динамической нагрузки на трибуны в виде последовательности полусинусоидальных импульсов:
|
|
|
t |
|
|
|
|
|
K |
p |
Gsin |
|
, |
0 t t |
p |
, |
|
|
|
|||||||
F t |
|
|
|
|
|
(1) |
||
|
tp |
|
|
|
||||
|
|
|
|
|
tp t Tp, |
|
||
0, |
|
|
|
|
|
|||
где Kp = Fmax / G — ударный фактор; Fmax — пиковое значение нагрузки; G — вес статической нагрузки на трибуны от зрителей; tp — продолжительность контакта; Tp — период импульсов. Отношение продолжительности контакта tp к периоду нагрузки Tp называется контактным отношением α = tp / Tp, частота импульсов равна fp =1 / Tp. Экспериментально установлено, что частота импульсов может принимать значения в пределах от1 до 4 Гц [13, 14, 21].
Аппроксимация (1) лежит в основе нормативных документов Великобритании, Канады, Германии и отражена в Еврокоде EN 1991-1-1 [12, 15, 4]. В нормах BS 6399-1:1996 приводится соответствие между различными видами контактных отношений и видами действий зрителей [5]: пешеходному движению и низкоритмичной аэробике соответствует значение
α= 2/3, ритмичным движениям и высокоритмичной аэробике — α = 1/2, обычным прыжкам —
α= 1/3, высоким прыжкам — α = 1/4.
Известно разложение функции F(t) в ряд Фурье [4]:
|
|
2 n |
|
2 n |
|
|
|
2 n |
|
|
|||||
F t G 1 an cos |
|
|
t bn sin |
|
|
t |
G 1 rn |
sin |
|
|
t n , |
(2) |
|||
T |
|
T |
|
|
|
||||||||||
|
n 1 |
p |
n 1 |
p |
|
|
n 1 |
T |
p |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где an , bn — коэффициенты Фурье, при 2n 1, an 0, bn 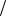 2, в остальных случаях
2, в остальных случаях
an |
cos 2n 1 1 |
cos 2n 1 1 |
, |
||||||
0,5 |
|
|
|
|
|
|
|
||
|
2n 1 |
|
2n 1 |
|
|||||
|
|
|
|
|
|
|
|||
bn |
sin 2n 1 |
1 |
sin 2n 1 1 |
, |
|||||
0,5 |
|
|
|
|
|
||||
2n 1 |
|
2n 1 |
|||||||
|
|
|
|
|
|
||||
rn 
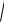 an2 bn2 , n arctg an
an2 bn2 , n arctg an 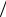 bn .
bn .
Анализ ряда (2) показывает, что импульсная нагрузка (1) удовлетворительно моделируется первыми шестью гармониками. На рис. 1 приведены графики функции F, кН/м2, от времени, c, полученные суммированием первых шести гармоник в (2) для α = 2/3 (пешеходное движение) и α = 1/4 (высокие прыжки) с частотой 2 Гц, статическая нагрузка от зрителей равна максимальному фактическому весу2,80 кН/м2.
Задача определения динамической реакции сооружения на воздействие (1) может быть решена несколькими способами. В качестве основного примем квазистатический метод, как наиболее удобный и хорошо знакомый инженерам-проектировщикам по задачам сейсмостойкости. Удобство квазистатического метода состоит в том, что внешние импульсные силы прикладываются к конструкции в виде статических нагрузок, внутренние усилия не зависят от времени, что упрощает конструктивные расчеты. Учет динамических эффектов в квазистатическом методе проводится с помощью коэффициентов динамичности. Квазистатический метод может рассматриваться с позиций детерминированного или вероятностного нагружения [19—21, 12]. В первом случае все параметры расчетной модели и нагрузки считаются строго определенными, а коэффициенты динамичности определяются методами теории
101

Научный журнал строительства и архитектуры
колебаний. Во втором случае нагрузка считается одной из реализаций случайного процесса, а коэффициенты динамичности зависят от его спектральной плотности. Проверочным расчетом будем считать прямое интегрирование уравнений движения во временной области с результатом в виде зависимостей параметров напряженно-деформированного состояния от времени. Ниже будут изложены три подхода к решению динамической задачи (квазистатический детерминированный, квазистатический вероятностный и проверочный во временной области) и проведен их сравнительный анализ. Помимо определения динамической реакции, оценивается комфортность пребывания зрителей на трибунах. По частотам и амплитудам виброперемещений и виброускорений устанавливается 6 градаций восприятия зрителями вибраций — от «вибрации не заметны» до «вибрации неприятны при кратковременном воздействии».
а) |
б) |
Рис. 1
1. Уравнения движения в главных координатах. Уравнение движения диссипатив-
ной системы с N степенями свободы имеет вид
Mq+Bq+Cq=P |
(3) |
где q — N-мерный вектор обобщенных перемещений; M, B, C — матрицы инерции, демпфирования и жесткости размерности N×N; P — N-мерный вектор обобщенных внешних импульсных сил. Вектор P состоит из периодических сил Pi, которые могут быть разложены в ряд Фурье по формуле (2):
G |
NF |
2 n |
|
|
||||
Pi t Pi |
1 rn |
sin |
|
|
n n , |
(4) |
||
|
|
|||||||
|
|
n 1 |
T |
p |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||
где PiG — статическая нагрузка от веса зрителей по i-й обобщенной координате; NF — ко-
личество удерживаемых членов ряда Фурье. В векторном виде
|
G |
G |
NF |
2 n |
|
|
|
P P |
P |
|
r sin |
|
n |
. |
|
|
|
||||||
|
|
|
n |
|
Tp |
|
n |
|
|
|
n 1 |
|
|
|
|
Обозначим: V — матрица |
собственных |
векторов |
системы (3) размерности N×N; |
||||
Ω2 diag 2k — диагональная матрица квадратов собственных частот; 2k — квадрат k-й
собственной частоты; Mmod — диагональная модальная матрица масс:
102

Выпуск № 1 (45), 2017 |
ISSN 2541-7592 |
Mmod VTMV diag Mmod,k ;
Mmod,k — модальная масса по k-й собственной форме; 2ε Mmod1 VTBV — модальная матрица демпфирования. Демпфирование предполагается малым, так что матрица демпфирования может считаться диагональной ε diag k , k — модальный коэффициент демпфирования по k-й собственной форме. При помощи преобразования q Vu получим систему независимых уравнений движения в пространстве главных координат:
u 2εu 2u Q, |
(5) |
где u — вектор главных координат; Q — вектор внешних импульсных сил, приведенный к главным координатам:
Q Mmod1 VTP.
В покомпонентном виде уравнение (5) имеет вид
u |
2 u |
2u |
Q |
, |
(6) |
|||
k |
k |
k |
k |
k |
k |
|
|
|
где |
Q |
|
1 |
|
vT P; |
|
|
|
Mmod,k |
|
|
||||||
|
k |
k |
|
|
|
|||
vTk — вектор k-й собственной формы. Решение в исходном базисе для j-й обобщенной коор-
динаты равно
qj vTju.
2. Квазистатическое детерминированное решение. Решение уравнения (5) в устано-
вившемся режиме вынужденных колебаний можно получить методом суперпозиции, учитывая разложение (4) и суммируя динамический отклик по каждой гармонической составляющей нагрузки (подробный вывод приведен в [5]):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T G |
|
|
|
|
rn sin n t n |
|
|
|
|
|||||
|
|
|
NF |
|
|
|
|
|
|||||||||
uk |
|
|
vk P |
1 |
|
|
|
|
|
|
|
|
|
|
, |
(7) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
n2 2 2 |
|
|
2 kn 2 |
||||||||||||
|
kMmod,k |
|
|
n 1 |
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
где n — фаза отклика на n-ю гармоническую составляющую нагрузки:
|
2 n |
|
n2 2 |
||
n |
n arctg |
k |
1 |
|
; |
2 |
2 |
||||
|
|
k |
|
k |
|
— угловая частота импульсной нагрузки:
2
2 fp .
Tp
Независящее от времени слагаемое в (7) соответствует статическому перемещению ust. Максимальное динамическое перемещение по k-й обобщенной координате umax,k найдем, положив синусы в (7) равными единице. Тогда модальный коэффициент динамичности, соответствующий k-й форме колебаний, равен
103

Научный журнал строительства и архитектуры
|
umax,k |
NF |
|
|
|
|
r |
|
|
|
|
||
|
1 |
|
|
|
|
|
|
. |
|||||
k |
|
|
|
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
st |
|
|
2 |
|
2 |
2 |
|
|
2 |
|
||
|
|
n 1 |
n |
|
|
2 n |
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
2 |
|
2 |
|||||
|
|
|
|
|
|
k |
|
|
|
k |
|
||
Эту формулу можно записать через модальный коэффициент затухания k ( k k k )
и частоты, выраженные в Гц ( fp 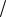 2 , fk k
2 , fk k 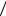 2 ):
2 ):
NF |
|
|
|
|
rn |
|
|
|
|
|
||
fk 1 |
|
|
|
|
|
|
|
|
. |
(8) |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
||||||
n 1 |
2 |
2 |
2 knfp |
2 |
|
|||||||
|
|
1 |
n |
|
fp |
|
|
|
|
|||
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
fk |
|
|
||||
|
|
|
fk |
|
|
|
|
|||||
На рис. 2 показаны графики коэффициентов динамичности в осях собственных частот β(fk) при частоте импульсов fp=2 Гц: а) для пешеходного движения α = 2/3 и б) для высоких прыжков α = 1/4; оба графика построены для случаев 5 % демпфирования (серая линия) и 2,5 % демпфирования (черная линия).
а) |
б) |
Рис. 2
3. Квазистатическое вероятностное решение. Случайный процесс, соответствующий импульсной нагрузке, узкополосный, то есть определен при дискретном наборе частот nθ в формуле (2). Спектральная плотность импульсной нагрузки представляет собой функции, близкие к δ-функции при координатах, соответствующих частотам воздействия nθ, n=1, …, NF. На рис. 3 представлены графики спектральных плотностей S, (кН/м2)2/Гц, соответствующие импульсным нагрузкам на рис. 1 при частоте импульсов fp = 2 Гц: а) для пешеходного движения α = 2/3, б) для высоких прыжков α = 1/4.
На временном интервале активного нагружения одним видом деятельности случайный процесс воздействия зрителей на трибуну можно считать стационарным, то есть среднее значение и стандарт процесса не зависят от времени. Среднее значение случайного процесса с учетом соотношений
Kp 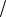 2 , tp
2 , tp 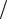 Tp
Tp
равно
|
1 |
Tp |
F t dt |
KpG |
Tp |
|
t |
|
|
mF |
|
|
sin |
dt |
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
|
Tp 0 |
|
Tp 0 |
tp |
|
||||
KpG |
2 |
tp |
G . |
(9) |
Tp |
|
|||
|
|
|
||
104
Выпуск № 1 (45), 2017 |
ISSN 2541-7592 |
Таким образом, нагрузку от согласованных действий зрителей можно рассматривать как стационарный случайный процесс со средним значением, равным величине статической нагрузки G.
а) |
б) |
Рис. 3
Движение системы (6) представим в виде |
|
|
u 2 u 2u |
Q, |
(10) |
где Q(t) — стационарный процесс на входе, соответствует внешнему воздействию на систему; u(t) — стационарный процесс на выходе, соответствует реакции (перемещению) системы.
Если известна спектральная плотность входного стационарного процесса SQ(θ), то спектральная плотность выходного процесса Su(θ) для линейной стационарной системы (10) определяется по формуле [1, 2]
SQ |
|
|
Su 2 2 2 |
4 2 2 . |
(11) |
Понятие коэффициента динамичности вводится по аналогии с детерминированными установившимися вынужденными колебаниями при гармоническом нагружении. Этот коэффициент показывает, во сколько раз надо увеличить статическую нагрузку, чтобы учесть динамические эффекты при квазистатическом подходе.
Выделим в правой части уравнения (10) постоянный множитель G — среднее значение случайной нагрузки Q, тогда обобщенная случайная сила равна
Q t GQ t .
Из линейности системы (10) следует
u t Gu t ,
где случайный процесс u есть перемещение от силы Q . Тогда вследствие стационарности входного и выходного процессов средний квадрат u2 (или дисперсия Du ) равен
2 |
D |
G2D |
|
. |
(12) |
u |
u |
u |
|
||
Коэффициент динамичности β при случайных нагрузках определяют как отношение стандарта динамического перемещения u к статическому перемещению uG (то есть к перемещению от статической нагрузки G):
105

Научный журнал строительства и архитектуры
|
|
|
|
|
|
|
|
|
|
u |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
uG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Квадрат стандарта 2 равен дисперсии выходного процесса |
D |
|
и связан со спектраль- |
|||||||||||||||||||||
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
ными плотностями Su |
и SQ . С учетом (12): |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
SQ |
|
|
|
|
|
|
||||||
2 |
|
2 |
|
|
|
2 |
S |
|
d G |
2 |
|
|
|
|
|
|
d . |
(14) |
||||||
u Du |
G |
|
D |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
u |
|
u |
|
|
2 |
|
2 |
|
2 |
2 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
4 |
|
|
|
|||||
Статическое перемещение uG не зависит от времени и определяется по уравнению (10) при Q = G:
u G 2 . |
(15) |
G |
|
Окончательный вид формулы для коэффициента динамичности системы с одной степенью свободы получается по определению (13) с учетом (14) и (15):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
SQ |
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
2 |
|
2 |
2 |
|
2 |
d |
. |
||||||
|
|
0 |
|
|
|
|
4 |
|
|
|
|||||||
Для многомерных систем, когда коэффициент динамичности свой для колебаний по каждой k-й собственной частоте, его принимают как функцию собственных частот Ωk:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|||||
k |
|
|
|
k SQ |
|
|
|
|
||||||
|
2 |
|
2 |
|
2 |
2 |
|
2 |
d |
. |
||||
|
|
0 |
k |
|
|
4 k |
|
|
|
|||||
Эту формулу можно записать через модальный коэффициент затухания k ( k k k )
и частоты, выраженные в Гц (SQ SQ f  2 , 2 f , k 2 fk ):
2 , 2 f , k 2 fk ):
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
SQ |
f |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
fk |
|
|
|
|
|
|
|
df . |
(16) |
|||
|
f |
2 |
|
2 |
f |
2 |
||||||
0 |
p |
4 2 |
p |
|
|
|||||||
|
|
1 |
|
|
|
|
|
|||||
|
f |
|
f |
2 |
|
|||||||
|
|
2 |
k |
|
||||||||
|
|
|
|
k |
|
|
|
k |
|
|
||
На рис. 4 показаны графики коэффициентов динамичности β(fk), построенные по формуле (16) при частоте импульсов fp = 2 Гц: а) для пешеходного движения α = 2/3 и б) для высоких прыжков α = 1/4. Черная линия соответствует 2,5 % демпфированию, серая линия — 5 % демпфированию.
4. Проверочный расчет во временной области и анализ результатов. На примере системы с одной степенью свободы рассмотрим, как квазистатические решения, изложенные в п. 3 и 4, соотносятся с проверочным расчетом во временной области. Формула (7) для установившихся перемещений одномассовой системы (10) имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
rn sin n t n |
|
|
|
|
|
||||||||||
|
|
NF |
|
|
|
|
|
|
|||||||||||||
u t |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(17) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n 1 |
|
2 |
|
2 |
|
2 |
2 n |
2 |
|
|||||||||
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
106

Выпуск № 1 (45), 2017 |
ISSN 2541-7592 |
Проверочный расчет выполняется для резонансного режима, когда частота импульсной нагрузки совпадает с собственной частотой системы: θ = Ω = 12,5664 рад/с (2 Гц). На рис. 5 показаны перемещения, м, в виде функции от времени, с, при пешеходном движении (а) и высоких прыжках (б) на интервале 10 с. Нагрузка G принята единичной. Определим по этим графикам вероятностный и детерминированный коэффициенты динамичности и сравним с коэффициентами, полученными в п. 2 (см. рис. 2) и в п. 3 (рис. 4).
а) |
б) |
Рис. 4
а) |
б) |
Рис. 5 |
|
|
Для пешеходного движения: амплитуда колебаний |
ua = 0,1624, среднее |
значение |
um = ust = 0,0063, стандарт σu = 0,1152; для частоты 2 Гц |
детерминированный |
КД равен |
βdet = ua /um = 25,78, вероятностный — βstoch = σu /um = 18,29. Соответствующие значения на |
||
диаграммах (см. рис. 2а, 4а): βdet = 26,79 (погрешность составляет 3,8 %), βstoch = 18,24 (погрешность — 0,3 %).
Для высоких прыжков: амплитуда |
колебаний |
ua = 0,2432, среднее |
значение |
um = ust = 0,0064, стандарт σu = 0,1689; для |
частоты 2 Гц |
детерминированный |
КД равен |
βdet = ua /um = 38,00, вероятностный — βstoch = σu /um = 26,39. Соответствующие значения на
107

Научный журнал строительства и архитектуры
диаграммах (см. рис. 2б, 4б): βdet = 39,44 (погрешность составляет 3,7 %), βstoch = 26,69 (погрешность — 1,1 %). Результаты проверки свидетельствуют о правильности двух изложенных подходов.
Следует отметить, что, как показано в [5], при импульсной спектральной плотности
stoch 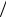 det 1
det 1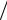

 2 0,707. Это связано с тем, что βstoch представляет собой стандарт случайного коэффициента динамичности. Отношение βstoch/βdet будет уменьшаться при учете случайного характера нагрузки.
2 0,707. Это связано с тем, что βstoch представляет собой стандарт случайного коэффициента динамичности. Отношение βstoch/βdet будет уменьшаться при учете случайного характера нагрузки.
5. Оценка восприятия вибраций зрителями. Тело человека представляет собой вяз-
коупругую систему, обладающую собственными частотами. Известны резонансные частоты отдельных органов тела человека [3]: глаза — 12—27 Гц, горло — 6—27 Гц, грудная клетка — 2—12 Гц, ноги и руки — 2—8 Гц, голова — 8—27 Гц, лицо и челюсти — 4—27 Гц, поясничная часть позвоночника — 4—14 Гц, живот — 4—12 Гц. При частотах колебаний, близких к резонансным, вибрации могут вызывать ряд негативных эффектов — от неприятных ощущений до серьезных функциональных и физиологических нарушений. Качественная оценка субъективных ощущений, вызванных действием вибраций, показана на рис. 6 [3] в виде областей равного восприятия: а) в зависимости от виброперемещения и частоты, б) в зависимости от виброускорения и частоты. Каждой области равного восприятия соответствуют различные уровни неприятных ощущений человека, перечисленные в табл.
а) |
б) |
Рис. 6
|
|
|
Таблица [3] |
|
|
|
|
|
|
Область |
Вибрация |
Область |
Вибрация |
|
1 |
Неощутимая |
4 |
Сильно ощутимая |
|
2 |
Слабо ощутимая |
5 |
Неприятная при длительном воздействии |
|
3 |
Хорошо ощутимая |
6 |
Неприятная при кратковременном воздействии |
|
При значительных уровнях вибрации в диапазоне 4—10 Гц человек может испытывать дискомфорт и болевые ощущения вследствие резонансных явлений системы «грудь — живот». Наиболее комфортное состояние при вибрациях с частотами от 1 до 4 Гц (вибрации не ощущаются) обеспечивается при значениях виброускорений до 1 см/с2, виброперемещений — до 1 мм. Эти данные совпадают с допустимыми виброускорениями, отраженными в санитарных нормах [11]. Таким образом, для оценки ощущений зрителей по рис. 6 и табл. необходимы амплитуды перемещений и ускорений. Амплитуды перемещений можно рассчитать по
108

Выпуск № 1 (45), 2017 ISSN 2541-7592
формуле (7). Дважды дифференцируя перемещения (7) по времени и полагая синусы равными единице, получим максимальное значение модального ускорения:
|
|
|
|
1 |
|
NF |
|
|
|
|
2 |
|
2 |
rn |
|
|
|
|
|
||
maxuk |
|
|
|
|
vTk PG |
|
|
|
|
n |
|
|
|
|
. |
(18) |
|||||
|
2 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
2 |
|
2 |
|
|
|
|
2 |
||||||||||
|
|
k |
mod,k |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
n 1 |
n |
|
|
|
|
2 n |
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
k |
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
k |
|
|
||||
Введем модальный коэффициент приведения статических перемещений к ускорениям Cacc (коэффициент, на который следует умножить статическое перемещение, чтобы получить максимальное ускорение):
NF |
|
|
|
n |
2 |
rn |
|
|
|
|
|
|
Cacc 2 |
|
|
|
|
|
|
|
|
. |
(19) |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
n2 2 2 |
|
|
|
|||||||
n 1 |
|
|
2 n 2 |
|
||||||||
|
|
|
1 |
|
|
|
|
k |
|
|
||
|
|
2 |
|
2 |
|
|||||||
|
|
|
|
k |
|
|
|
k |
|
|
||
Коэффициенты Cacc определяются для каждой собственной частоты (рис. 6) и поэтому так же, как коэффициенты динамичности, являются модальными. Пример диаграммы Cacc на рис. 6 приведен для частоты импульсов fp =2 Гц: а) для пешеходного движения α = 2/3 и б) для высоких прыжков α = 1/4. Черная линия соответствует 2,5 % демпфированию, серая — 5 % демпфированию. По значениям динамических перемещений и ускорений при известной частоте воздействия по табл. и рис. 6 определяется уровень восприятия вибраций зрителями.
а)
б)
Рис. 7
109

Научный журнал строительства и архитектуры
Выводы. В ходе исследования выяснились некоторые особенности нагрузки от согласованных действий зрителей:
1.Импульсное воздействие (1) обладает таким свойством, что при одной частоте импульсов возбуждаются сразу несколько форм колебаний конструкции. Так, если зрители синхронно совершают высокие прыжки с частотой 2 Гц, резонансы будут наблюдаться не только при собственных частотах конструкции 2 Гц, но и на 4, и на 6, и на 8 Гц, если такие имеются (рис. 2, 4). Наиболее опасная ситуация соответствует случаю, когда спектр собственных частот накладывается на диапазон возможных частот вынужденных колебаний 1— 4 Гц. При этом коэффициенты динамичности достигают максимальных значений. Как отмечается в [5], в этом случае динамический расчет нецелесообразен, необходимо заранее принимать меры по отстройке от резонанса. Динамическая реакция возрастает, если велики статические перемещения (особенно для консольных конструкций);
2.Нагружение узкополосное, то есть вся энергия импульсов сосредоточена на четко определенных частотах nf, а спектральная плотность воздействия представляет собой последовательность импульсных функций на этих частотах, n = 1, 2, …, NF. По этой причине ко-
эффициенты динамичности получились необычно высокими: до 14 при 5 % и до 26 при 2,5 % демпфировании в резонансном режиме при пешеходном движении, до 20 при 5 % и до 39 при 2,5 % демпфировании в резонансном режиме при высоких прыжках. Следует отметить, что такие значения коэффициентов динамичности соответствуют абсолютно синхронным движениям людей с одной и той же фазой, частотой и амплитудой, что, очевидно, маловероятно. Обоснованно снизить коэффициенты динамичности можно, учитывая рассогласованность движений людей. В зарубежных методиках предлагается умножать параметры динамической реакции на коэффициент несинхронности, равный 0,67 [12]. Однако этот вопрос можно решить точнее, вводя случайные параметры динамической нагрузки, такие как амплитуда, фаза движений, а также пространственное распределение. При этом спектральная плотность примет более сглаженный вид, ординаты пиков снизятся, а коэффициенты динамичности уменьшатся;
3.Для снижения амплитуд колебаний имеет смысл применять технологии, повышающие демпфирующие свойства конструкции;
4.Поскольку уровень вибраций может быть велик и неприятен для зрителей, необходимо дополнять расчет оценкой уровня ощущаемых вибраций. Отметим, что если следовать санитарным нормам [11], то конструкция трибун должна обеспечивать уровень «вибрации не ощущаются», что для спортивных сооружений часто является слишком жестким условием.
Библиографический список
1. Болотин, В. В. Методы теории вероятностей и теории надежности в расчетах сооружений / В. В. Болотин. — Изд. 2-е, перераб. и доп. — М.: Стройиздат, 1982. — 352 с.
2.Болотин, В. В. Статистические методы в строительной механике / В. В. Болотин. — М.: Стройиздат, 1961. — 160 с.
3.Вибрации в технике: справочник: в 6 т. Т. 6. Защита от вибрации и ударов. — М.: Машиностроение, 1981. — 456 c.
4.Гульванесян, Х. Руководство для проектировщиков к Еврокоду 1. Воздействия на сооружения. Разделы EN 1991-1-1 и с 1991-1-3 по 1991-1-7 / Х. Гульванесян, П. Формичи, Ж. А. Калгаро. — М.: МГСУ, 2011. — 264 c.
5.Назаров, Ю. П. Динамика спортивных сооружений / Ю. П. Назаров. — М.: Наука, 2014. — 222 c.
6.Назаров, Ю. П. Расчетные модели сейсмических воздействий / Ю. П. Назаров. — М.: Наука, 2012. —
414 c.
7.Назаров, Ю. П. Экспертная оценка конструктивных решений Центрального стадиона и Большой ледовой арены для хоккея с шайбой в г. Сочи / Ю. П. Назаров, Ю. Н. Жук, В. Н. Симбиркин, А. В. Ананьев, В. В. Курнавин // Актуальные проблемы исследований по теории сооружений: сб. науч. ст.: в 2 ч. Ч. 2 / ЦНИИСК им. В. А. Кучеренко. — М.: ЦПП, 2009. — С. 8—16.
8.Назаров, Ю. П. Определение коэффициента динамичности в расчетах на сейсмостойкость [Электронный ресурс] / Ю. П. Назаров, Е. В. Позняк // Строительство: наука и образование. — 2015. — № 1 // Строи-
110
