3127
.pdf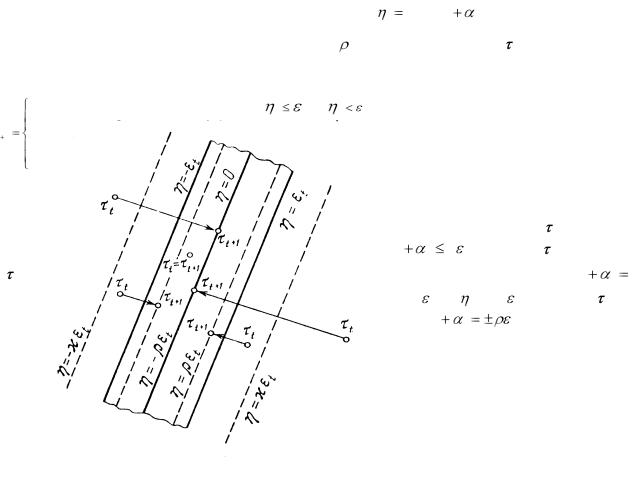
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t (at , τt ) |
t . |
|
|
|
(3.22) |
||||
Пусть κ — произвольное число, κ > min (1, 2 |
). Для произвольного |
0 следующий |
КСА |
||||||||||||||||||||||
решает условные неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(3.14) |
(по теореме 2.1.1 /33/) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
τt , |
если |
|
t |
|
|
t ( |
|
t |
|
t ), |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
τt 1 |
τt |
|
|
|
|
|
|
|
|
|
|
|
|
|
23) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
τt |
|
|
|
|
|
|
|
|
|
|
|
|
случаю, когда |
в (3.19) |
знак «мень- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ше». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 3.1). Если точка |
t |
находится в |
|||||||
полосе (3 |
|
|
|
|
|
|
|
|
|
|
t |
|
κ |
t , то точка |
t +1 получается |
||||||||||
|
|
|
|
|
|
|
|
|
|
) |
|
||||||||||||||
из t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19), т.е. на плоскость (at , τ ) |
t |
0 . |
|||||||
Если же |
|
|
|
|
|
|
|
|
|
|
если |
t |
<| |
t| < κ |
t ), то точка |
t+1 по- |
|||||||||
лучается |
|
|
|
|
|
|
|
|
|
|
(at , τ ) |
|
t |
t . |
|
|
|
|
|||||||
Вектор t +1 всегда лежит в полосе (3.19). Таким образом, алгоритм (3.23) можно применять для решения безусловных рекуррентных неравенств, если только неравенство (3.19) относится к моменту времени t+1.
В частном случае можно взять κ = , тогда второй случай в (3.23) будет всегда отсутствовать и алгоритм (3.23) примет вид:
τt 1 |
τt |
|
|
|
|
|
если |
τt |
( t |
tsign t )at |
|
at |
|
2 , если |
|
|
|
t 
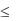t
t 
t
( |
|
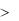t |
|
t ), |
||
|
|
|||||
( |
|
|
t |
|
|
t ). (3.24) |
|
|
|
|
|||
Алгоритм предполагает знание числа , определяющего «запас» выполнения неравенств для некоторого = *.
Если < 1/2, то можно взять κ < 1; в этом случае алгоритм (3.23) приобретает особенно простой вид
τt 1 |
τt |
, |
|
|
|
|
если |
τt |
t at |
|
at |
|
2 , |
если |
|
|
|
||||||
|
|
|
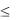t 
t
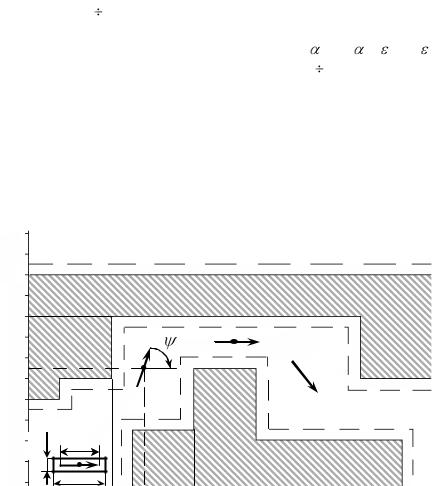
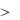t 
t
( |
|
|
t |
|
t |
), |
(3.25) |
|
|
|
|||||
( |
|
t |
|
|
t ). |
||
|
|
|
|
||||
Геометрическая интерпретация алгоритма (3.25) состоит в следующем: значение t + 1 сов-
падает с t , |
если выполнено неравенство (3.19), и получается из t проектированием на плос- |
|
кость (at , τ ) |
t |
0 в противном случае. |
Алгоритм, |
доставляющий значения at , t , t , может быть и таким, что эти значения зави- |
|
сят лишь от t, в этом случае неравенства (3.19) по существу заданы заранее; каждый из алго-
82
ритмов (3.23) (3.25) доставит через конечное число шагов решение всех этих неравенств. В особенно простом случае неравенства (3.19) получаются циклическим повторением заданной конечной системы неравенств (т.е. at + T =at , t + T = t , t + T = t для некоторого натурального Т). Таким образом, каждый из алгоритмов (3.23) (3.25) может быть использован для решения конечной заданной системы неравенств (3.19).
Алгоритм «Полоска - 1» позволяет рассчитывать программные задания на движение мобильного робота в зоне, свободной от препятствий, за короткий интервал времени.
3.5. Построение программных движений самоходной тележки
Рассмотрим задачу построения ПД тележки, передвигающейся по цеху с препятствиями
(см. рис. 3.2).
Y,
м
10 di
8
y
6
ci 
b a - b
2
а |
3.1.1.2 Рис. 3.2. Тележка на участке с препятствиями
Положение тележки на плоскости 0XY определяется вектор-функцией
z(t) (x(t), y(t)),Ψ (t)), |
(3.26) |
где x, у — координаты центра масс тележки;
— курсовой угол тележки.
Программным движением zp(t) (t [t0, tT]) транспортной тележки будем называть такое ее допустимое движение, которое обеспечивает переход робота из произвольного начального состояния z(t0), z (t0) в желаемое конечное состояние z(tT), z (tT), при котором выполняется целевое условие.
Препятствия аппроксимируем на плоскости 0XY с помощью прямоугольников. Прямоугольные зоны, свободные от препятствий, характеризуются параметрами аi, bi, сi, di. Для обеспечения движения центра масс тележки без столкновения с препятствиями должны быть
84
выполнены условия:
если аi< x<bi, то ci<y<di при всех i. |
(3.27) |
Окружим препятствия такой - окрестностью, чтобы достаточно было следить не за движением всей тележки, проекция которой на плоскость ОХY имеет форму прямоугольника, а только за имитирующим ее вектором длины (с модулем l=|а-b|), проходящим через центр масс тележки с тем же курсовым углом. Величину можно взять равной 1/2min(а, b), где а и b — длины сторон проекции тележки.
Функцию изменения курсового угла ПД тележки будем искать в виде полинома
N |
|
|
ψP(t) ψP(t0 ) |
bj(t t0 ) j , |
(3.28) |
j |
1 |
|
где р(t0) — начальное значение курсового угла; bj — искомые параметры движения.
При равномерном движении тележки вдоль оси 0X координата xp(t) центра масс определяется из выражения
xP (t) xP (t0 ) T 1[xP (tT ) xP (t0 )](t t0 ), t [t0, tT], (3.29)
где xр(t0) и xр (tT) — начальное и конечное значения координаты x центра масс тележки; Т — период времени движения.
Программное движение центра масс тележки вдоль оси 0Y определяется интегральной за-
85
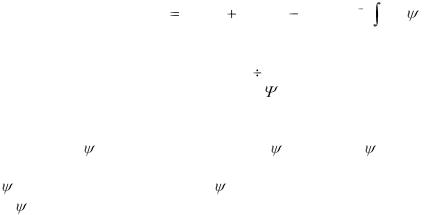
висимостью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
y |
P |
(t) |
y |
P |
(t |
0 |
) |
(x |
P |
(t ) |
x |
P |
(t |
0 |
))T 1 |
tg( р(t))dt, |
(3.30) |
|
|
|
|
|
|
T |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
где yр(t0) — начальное значение координаты y центра масс тележки. |
|
|
|
|
|||||||||||||
ПД тележки, выбранное в классе функций (3.28) |
|
(3.30), обеспечивает перемещение те- |
|||||||||||||||
лежки в направлении, соответствующем курсовому углу |
р(t). Параметры bj ( j = 1, ... N ) поли- |
||||||||||||||||
нома вида (3.28) необходимо выбрать так, чтобы удовлетворить условиям (3.27) обхода препятствий.
Текущим значениям t и (t) соответствуют xр (t, (t)) и yр (t , (t )), вычисляемые из (3.29), (3.30). При этом для i-ой свободной от препятствий прямоугольной зоны, определяемой из условия аi <xр (t, (t))<bi для координаты yр (t, (t)) согласно (3.27) должно выполняться неравенство ci <yр (t, (t))<di . Для определения параметров bj, обеспечивающих выполнение этих неравенств, используется конечно-сходящийся алгоритм «Полоска - 1» /33/, описанный в предыдущем пункте.
3.6. Построение программных движений манипулятора
Для проведения погрузочно-разгрузочных работ в цехе мобильному роботу достаточно иметь трехкоординатный манипулятор с цилиндрической системой координат.
Положение манипулятора мобильного робота в момент времени t однозначно определяется вектором обобщенных ко-
86
ординат q(t)=|qj(t)| nj 1 или вектором декартовых координат рабочего |
органа s(t)=|si(t)| ip |
1 . |
Движение манипулятора одно- |
|
|
значно определяется функциями q(t), q (t). |
|
|
Программным движением манипулятора мобильного робота qр(t), t |
[t0, tT] будем называть |
|
такое его допустимое движение, которое обеспечивает переход схвата из произвольного начального состояния q(t0), q (t0) в желаемое конечное состояние q(tT), q (tT), при котором выпол-
няется целевое условие.
С точки зрения построения траекторий, обеспечивающих огибание препятствий (станков),
наиболее интересны вертикальное и горизонтальное движения |
манипулятора. |
|
На |
установленный на |
тележке, препятствие и система |
y,
м
1
0 |
1 |
2 |
x, м |
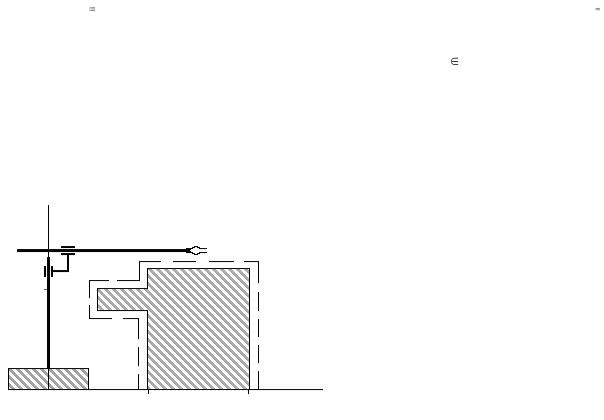
3.1.1.3 Рис. 3.3. Манипулятор мобильно-
Положение схвата манипулятора определяется в момент времени t формулами
xP (t) |
r0 |
q1 (t), |
(3.31) |
yP (t) |
l0 |
q2 (t), |
(3.32) |
где xp (t ), уp (t ) — координаты схвата манипулятора; r0, l0 — конструктивные параметры манипулятора.
При движении манипулятора, представленного на рис. 3.3, отсутствие касания схвата о препятствие означает, что и все другие точки манипулятора не будут сталкиваться с препятствием.
Препятствие аппроксимируем прямоугольниками, стороны которых параллельны координатным осям, и окружим -областью. Величина выбирается в зависимости от размеров кассеты с деталями, которую должен переместить манипулятор. Параметры препятствий заносятся в
массив чисел {аi , bi , сi ,di } iN1 таких, что выполнены условия
если ci <y<di , то аi <x<bi при всех i. |
(3.33) |
В данном случае неравенства (3.33) должны быть выполнены для точки в центре схвата с
88
координатами xP (t), yP (t) при каждом t [t0, tT].
Примем для упрощения решения задачи движение yр(t) вдоль оси 0у равномерным:
y |
P |
(t) |
y |
P |
(t ) |
( y |
P |
(t ) |
y(t ))(t |
t )T 1, |
(3.34) |
|
|
|
||
|
|
|
0 |
|
T |
0 |
0 |
|
|
|
|
|
|
|||
где yр(t0) и yр(tТ) — начальное и конечное состояния по координате 0у, |
|
|
||||||||||||||
Т — время выхода в заданное положение по оси 0у. |
|
|
|
|
|
|||||||||||
Движение хр(t) вдоль оси 0х будем искать в виде полинома |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
P |
(t) |
b t i |
, |
(3.35) |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
0 |
|
|
где bi — искомые параметры ПД. |
|
|
ci < yр(к) < di. Тогда для |
|
||||||||||||
Пусть параметры препятствий такие, что |
координаты 0х |
|||||||||||||||
должны выполняться |
неравенства |
аi <xр(к) <bi при всех i, которые линейны относительно не- |
||||||||||||||
известных коэффициентов полинома (3.35).
Система полученных линейных неравенств, порожденных препятствиями, разрешима, если только целевое условие вообще выполнимо в рассматриваемом классе движений (3.35). Применяя для решения полученной системы неравенств конечно - сходящийся алгоритм «Полоска - 1» (явные формулы которого приведены в п. 3.4.), получим после конечного числа коррекций искомые значения параметров bi ПД вида (3.35). Полученное программное движение, определяемое неравенствами (3.34), (3.35), достаточно плавное и удовлетворяет условиям
(3.33).
89
Выполнение целевого условия манипулятором осуществляется в общем случае не единственным способом. Разные варианты траекторий возникают при изменении начальных параметров bi.
3.7.Сплайн-интерполяция задающих сигналов
Врезультате решения обратной задачи кинематики формируется массив значений обобщенных координат в ряде опорных точек на траектории движения манипулятора. Интерполяция траектории между опорными точками при планировании движений осуществляется с помощью сплайн-функций /23, 25/.
Рассмотрим задачу о приближении функции qj (t ) на отрезке времени [0, T ]. Отрезок разбит на части
[t0, t1], [t1, t2], ... , [ts-1, ts], … , [tm-1, tm], |
(3.36) |
причем t0=0, tm=T.
Сплайном S (qj ,t) порядка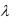 
называется функция, являющаяся многочленом степени 
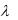на каждом из временных интервалов [ts-1, ts]:
S (qj, t) = Pj,s (t)=aj,s0+, ... ,+ a j,s t , ts-1<t<ts, (3.37)
удовлетворяющая условиям непрерывности самой функции и непрерывности ее производных до порядка -1 в точках t1, t2, ... , t m -1 :
90