2706

P

Рис.2.12. Схема определения напряженности электрического поля внутри равномерно заряженной сферы

Построим два концентрических конуса, направленных в противоположные стороны с общей вершиной в точке P . Эти конусы вырезают площадки на противоположных сторонах сферы. Поскольку заряд распределен по поверхности сферы равномерно, сила, действующая на пробный заряд от каждого из вырезанных сегментов шара, пропорциональна площади сегмента. Обе силы направлены противоположно друг другу. Но сегмент с большей площадью отстоит от точки P дальше, чем сегмент с меньшей площадью. Увеличение силы, действующей на пробный заряд, с ростом площади сегмента (пропорционально r2 ) компенсируется уменьшением её из-за большей удаленности сегмента (пропорционально 1r2 ). В результате обе силы оказываются равными так, что результирующая сила равна нулю. Эту аргументацию можно распространить и на остальную поверхность сферы. В результате оказывается, что на пробный заряд не будет действовать сила. Точно такой же вывод получается и для всех прочих точек внутри шара. Следовательно, электрическое поле внутри сферической оболочки отсутствует. Применяя более сложный математиче-

81

ский метод, можно получить такой же результат не только для сферы, но и для любой другой замкнутой поверхности.

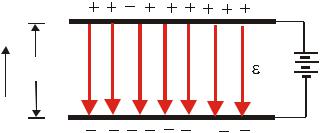
2. Электрическое поле между двумя равномерно заряженными параллельными пластинами одинаковой площади однородно (рис.2.11,е). Рассмотрим случай, когда обе пластины имеют бесконечную протяженность, причем одна из них равномерно заряжена положительным, а другая - равным по величине отрицательным зарядом. Вследствие того, что пластины заряжены равномерно, любой участок между пластинами ничем не отличается от других участков. Следовательно, силовые линии должны быть распределены равномерно и параллельно друг другу.

В реальном случае, когда пластины имеют конечный размеры, силовые линии на краях пластины искривляются. Однако если расстояние между пластинами мало по сравнению с размерами самих пластин, то этот краевой эффект оказывается несущественным. Разность потенциалов между двумя точками называется напряжением между этими точками:эл V . Допустим, у нас имеется пара параллельных пла-

стин на расстоянии d друг от друга (рис.2.13). Если пластины присоединить к батарее, то пластина с положительным зарядом примет потенциал элA , а пластина с отрицательным заря-

дом – потенциал Bэл так, что

где V - напряжение батареи.

Электрическое поле между пластинами определяется электрической силой, действующей на пробный заряд в этом поле:

82

Рис.2.13. Схема электрического поля между двумя параллельными разноименно заряженными пластинами

При перемещении пробного заряда из B в A надо совершить работу против действующей на q электрической силы. Эта работа равна

Работа на единицу заряда WA B q есть просто напряже-

ние V , так что в однородном поле

2.5. Поле ядерных сил

Гравитационное поле шарообразного тела или электрическое поле сферического заряда имеют чрезвычайно простой характер. Напряженности таких полей убывают с расстоянием по тому же геометрическому закону, что и интенсивность, например, света, излучаемого источником равномерно по всем направлениям в пространстве. Этот закон пропорциональности

83

напряженности поля по величине 1r2 говорит о том, что на каком бы конечном расстоянии от источника поля ни находилось пробное тело, оно везде будет испытывать действие силы. Эта сила обращается в нуль только на определенном расстоянии r .

Ядерные силы имеют совершенно иной характер. Действие этих сил не простирается до бесконечности; напротив, оно ограничено чрезвычайно малой областью, окружающей источник. Какова природа ядерного поля? И вообще пригодно ли понятие поля для описания ядерных сил?

Представление о поле применимо к большим по величине ядерным силам, но характер проблемы в этом случае требует совершенно иных рассуждений. Основная идея природы ядерных сил была высказана в 1935 году японским физиком Хидеки Юкава (1907 г.). Он предположил, что два нуклона испытывают притяжение на малых расстояниях благодаря взаимному обмену гипотетической в то время элементарной частицей, названной мезоном. Эта частица имеет массу, промежуточную между массами электрона и протона. Поэтому она и была названа мезоном: «мезос» по-гречески значит средний. В настоящее время известно несколько разновидностей мезонов. Те мезоны, которые ответственны за ядерные силы, имеют массу, примерно в 273 раза превышающую массу электрона, т.е. составляют около 15% массы протона. Они называются - мезонами или пионами. Пионы – основные частицы, ответственные за ядерные силы, но теперь известны и другие более массивные мезоны, которые вносят свою долю в сильное ядерное взаимодействие.

Детальное исследование пионных обменных сил требует привлечения сложного математического аппарата, поэтому ограничимся качественным описанием этого типа обменных сил. Предположим двух игроков, перебрасывающих друг другу мяч. Мяч постоянно перебрасывается, не задерживаясь у какого-либо игрока. Оба игрока оказываются как бы привязан-

84

ными друг к другу в результате такого постоянного обмена мячом. Можно сказать, что в этом случае действует «обменная баскетбольная сила».

А теперь представим, что сталкиваются два нуклона - протон и нейтрон. Процесс столкновения управляется ядерной силой (пионной обменной силой), действующей между обеими частицами. Где находится пион, который является посредником в этом взаимодействии? Он всегда «где-то здесь». Очень удобно представлять протон, как бы состоящим из нейтрона и положительно заряженного пиона:

Иными словами, протон как бы состоит из нейтронного остова, окутанного мезонным облаком. Или, на языке поля, можно говорить, что вокруг нейтрона существует пионное облако и в целом такое образование является протоном. При столкновении протона и нейтрона происходит обмен - мезоном между двумя нейтронами, и этот мезон осуществляет ядерное взаимодействие между частицами. Процесс обмена пионом является чрезвычайно быстрым; он происходит за время порядка 10-23 с.

Но протон и нейтрон различаются по массе лишь на 0,1%. Можно ли в этом случае считать, что протон состоит из нейтрона и пиона, если масса пиона достигает 15% массы протона? Для ответа на этот вопрос необходимо обратиться к принципу неопределенности квантовой механики.

Этот принцип утверждает, что процесс p n , в котором масса не сохраняется, возможен, если в течении короткого промежутка времени происходит и обратный процесс n p, в результате чего все возвращается в исходное состояние. Обмен пионом между сталкивающимися нейроном

и протоном разрешен, поскольку процесс обмена завершается за время порядка 10-23с.

85

Представление о том, что в основе ядерных сил лежит пионное поле, позволило достигнуть больших успехов, хотя многое еще не ясно. Более скромными являются наши знания в области слабых ядерных взаимодействий. Скорее всего, существует элементарная частица, которая переносит взаимодействие между электронами и нейтрино, но о природе этой частицы еще нет четкого представления.

2.6. Энергия поля

Если тело поднято на высоту hнад поверхностью Земли, то говорят, что тело обладает гравитационной потенциальной энергией mgh. Но обладает ли тело на самом деле этой потенциальной энергией? Может быть, ему приходится разделять эту потенциальную энергию с Землей? В соответствии с описанием гравитационного взаимодействия на основе понятия поля мы не должны приписывать изменения потенциальной энергии какому бы то ни было телу. Для изменения относительного положения двух тел следует совершить работу mgh над полем, и эта работа перейдет в энергию гравитационного поля. Энергию поля можно извлекать, создавая условия, при которых поле приводит тела в движение. Аналогичные соображения применимы к электрическому полю и полю ядерных сил. Но, помня, что поле обладает потенциальной энергией, все же будем следовать обыкновению и говорить о потенциальной энергии тела или системы тел. Но может быть это заблуждение, говорить, что поле обладает энергией? Как может пустота, в которой нет никаких материальных частиц, обладать столь реальной физической характеристикой, как энергия?

Рассмотрим следующую ситуацию. Космический корабль после прилунения передает на Землю информацию с помощью радиоволн, которые представляют собой распространяющиеся в пространстве возмущения электромагнитного

86

поля. Передатчик посылает сигнал, который содержит некоторое количество энергии. Этот сигнал распространяется со скоростью света и спустя 1,3 с достигает приемника. Где находилась энергия в течении 1,3 с , прошедших с момента её посыла до момента её приема? Согласно закону сохранения энергии, она должна была где-то быть. В действительности она могла содержаться только в электромагнитном поле.

Собрав все известные нам виды энергии и переименовав «потенциальную энергию» в «энергию поля», получим такой перечень:

1.кинетическая энергия,

2.энергия поля,

3.собственная энергия.

До сих пор теоретический подход к физическим явлениям на основе представления о поле оказывается столь успешным и плодотворным, что можно ожидать дальнейшего его развития, которое позволит объединить все известные виды энергии в единую концепцию энергии поля. В этом случае появилась бы возможность рассматривать все виды энергии на единой основе, вне зависимости от источника энергии.

2.7. Дифференциальные операции в скалярных

ивекторных полях

2.7.1.Скалярное поле

Пусть V - область в трехмерном пространстве (или на плоскости). Говорят, что в области V задано скалярное поле, если каждой точке M V поставлено в соответствие некоторое число U(M).

Поверхность (линия), на которой функция U(M) принимает постоянное значение, называется поверхностью (линией) уровня скалярного поля (например, поверхность или линия постоянной температуры). Придавая U(M) различные посто-

янные значения:U(M) C , получим семейство поверхностей (линий) уровня данного скалярного поля.

Физические скалярные поля не зависят от выбора системы координат: величина U является функцией лишь точки M и, быть может, времени (нестационарные поля).

Если в пространстве введена прямоугольная система координатOxyz, то скалярное поле описывается функцией трех переменных: U U(x,y,z); (x,y,z) V .

2.7.2. Векторное поле

Говорят, что в области V задано векторное поле, если

коллинеарности вектора поля aи касательного вектора r(t)в произвольной точке этой линии имеет вид

где - некоторое число. Условие (2.26) можно также записать в виде равенства нулю следующего векторного произведения:

Каждое из приведенных уравнений является дифференциальным уравнением векторных линий в векторной форме и определяет множество векторных линий.

Конкретная векторная линия, проходящая через заданную точкуM0 , определяется дополнительным условием

где r - радиус-вектор точкиM .

Физические векторные поля не зависят от выбора системы координат: в каждой точке M вектор a(M)полностью

определяется своим модулем a(M) и направлением. Если в

пространстве введена прямоугольная система координат, то векторное поле a(M)описывается вектор-функцией трех переменных или тремя скалярными функциями - ее координатами:

a(x,y,z) P(x,y,z),Q(x, y,z),R(x, y,z) ;(x, y,z) V .

В прямоугольных координатах dr dx,dy,dz , поэтому векторное уравнение (2.27) для векторных линий эквивалентно системе дифференциальных уравнений

где x0, y0,z0 - координаты точкиM0 .

2.7.3. Производная по направлению

Скалярное и векторное поля U(M) U(x,y,z) и a(M) P(x, y,z),Q(x, y,z),R(x, y,z) называются дифференцируемыми n раз, если функции U(x, y,z), Q(x,y,z),R(x,y,z) дифференцируемы n раз.

В дальнейшем, не оговаривая это особо, будем считать, что рассматриваемые поля дифференцируемы нужное нам число раз.

Пусть U(M) - скалярное поле, заданное в области V , а e - единичный фиксируемый вектор; M - фиксированная точка, M - любая точка из V, отличная от M ,и такая, что вектор MM коллинеарен вектору e .

Знак « + » в знаменателе последней дроби берем в том случае, если векторы MM и e сонаправлены и «-» в противном случае.

U

Производная по направлению e является скоростью

изменения функции U(M) по направлению e в точкеM . Если e cos ,cos ,cos в прямоугольной системе координат Oxyz ,

Точно так же определяется производная векторного поля e(M) в направлении вектора e .

ли 0, т.е. в том случае, если направление вектора e совпадает с направлением вектораc .

Вектор c , определяющий направление наибольшего роста поляU , называется градиентом скалярного поля и обозна-

U U U

чается gradU , , .

x y z

Тогда формула (2.31) может быть записана следующим образом

91

стемы координат, а его модуль и направление в каждой точке определяются самой функцией U(M) .

Иногда потенциалом векторного поля aназывают такую функциюU , чтоa gradU . Поверхности уровня потенциала

U(M)называют эквипотенциальными.

92

2.7.6. Дивергенция

Дивергенцией векторного поля

Дивергенция означает «расходимость». Дивергенция характеризует плотность источников данного векторного поля в рассматриваемой точке.

Векторное поле называется соленоидальным в областиV , если в этой области diva 0.

Так как diva характеризует плотность источников поля a, то в той области, где поле aсоленоидально, нет источников этого поля.

Векторные линии соленоидального поля не могут начинаться или заканчиваться внутри области соленоидальности; они либо начинаются и заканчиваются на границе области, либо являются замкнутыми кривыми.

2.7.7. Ротор

PQ R

Вчастности, для плоского поля

93

Ротор характеризует завихренность поля в данной точке. Рассмотрим твердое тело, вращающееся вокруг оси Oz с постоянной угловой скоростью . Векторное поле скоростей

v(M) точек этого тела можно представить в виде

Найдем ротор поля скоростей v(M) :

Таким образом, rotv является постоянным вектором, направленным вдоль оси вращения Oz, а его модуль равен

94

z

k

y

x

Рис. 2.14

Вычислим ротор поля r . Вообще ротор любого потенциального поля равен нулю, поэтому говорят, что потенциальное поле является безвихревым.

Если векторное поле a(M) можно представить как ро-

тор некоторого векторного поля b(M), т.е.a rotb , то век-

тор-функция b(M) называется векторным потенциалом поля a(M).

2.7.8. Примеры решения задач

Задача 1. Найти и нарисовать линии уровня скалярного поляU xy . Вычислить и изобразить на чертеже градиент этой функции в точках (1; 1) и (1;-1).

Решение. Линии уровня функции U xy задаются уравнением xy C , где C - произвольная постоянная. Графически это уравнение представляется семейством гиперболы

В точке (1; 1) функция быстрее всего возрастает в направлении от начала координат по биссектрисе I квадранта, и скорость ее возрастания в этом направлении равна

В точке (1;1) функция быстрее всего возрастает в направлении от начала координат по биссектрисе IV квадранта и скорость ее возрастания в этом направлении также рав-

на2 .

Задача 2. Найти производную функции

U x2 y2 z2 a2 b2 c2

в данной точке P0(x0, y0,z0) в направлении радиуса-

вектора r0 этой точки. В каком случае эта производная будет равна величине градиента?

Решение.

96

Пусть a b c, тогда

т.е. производная в направлении радиус-вектора для функции

U x0 y0 z0 a2 b2 c2

совпадает с величиной градиента этой функции при условии a b c.

Задача 3. Найти векторные линии векторного поля

a(M) gradu, где u xyz .

Решение.

a(M) grad(xyz) yzi xzj xyk .

Уравнение векторных линий находим, пользуясь (1.29)

Эти уравнения определяют два семейства гиперболических цилиндров с образующими параллельными, соответствующим осям Oz иOx, а при условии c1 c2 0 - две пары плоскостей x y; y z.

Любая векторная линия поля a(M) является линией пересечения двух поверхностей из полученных двух семейств при некоторых фиксированных значениях c1 и c2 . Например,

при c1 c2 0 линия пересечения плоскостей x y и y z представляет собой прямую, проходящую через начало координат. Ее уравнение имеет вид: x y z. В точках этой прямой вектор поля a(M) x2,y2,z2

Задача 4. Найти дивергенцию векторного поля

интегрируя, а затем потенцируя, получаем

c

ln f (r) 3lnr lnc; f (r) - это кулоновское поле. r3

Задача 6. Дано векторное поле a yzi zxj xyk. Найти rota в точке M(1,0,3).

Решение. Согласно определению ротора, имеем

Во всех точках заданного поляrota(M) 0, т.е. поле является безвихревым или потенциальным.

Задача 7. Найти ротор сферического векторного поля

Итак, ротор любого сферического векторного поля равен нулю, т.е. сферическое векторное поле является безвихревым.

99

2.8. Интегральные характеристики векторных полей 2.8.1. Поток векторного поля

Рассмотрим векторное полеa(M), определенное в пространственной области G , и некоторую кусочно-гладкую ориентированную поверхность G . Пусть n(M) - поле единичных нормалей на выбранной стороне поверхности . По определению

называется потоком векторного поля a(M) через поверхность в сторону, определяемую вектором n (говорят также: «поток через выбранную сторону поверхности »).

Если взять другую сторону поверхности (изменить ориентацию), то вектор n изменит направление на противоположное, поэтому скалярное произведение a n , а значит и поток (поверхностныйинтеграл (2.44)) изменит знак.

Если a v - скорость движущейся жидкости, то

v ndS представляет собой количество (объем) жидкости,

протекающей через поверхность в заданную сторону в единицувремени. Эта величина называется в физике (гидродинамике) потоком жидкости через поверхность . Поэтомуи в случае произвольного векторного поля a(M) интеграл (2.44) называется потоком векторного поля через поверхность .

Рассмотрим электрическое поле E точечного заряда e,

помещенного в точку N . Найдём поток векторного поля E через внешнюю сторону сферы радиуса r с центром в точ-

ке N . Пусть r NM (M - точка на сфере ); тогда

100