
Силовой расчет и динамика манипуляционных механизмов. Рябцев В.А., Трубецкой В.А
.pdf
В. А. Рябцев В. А. Трубецкой
СИЛОВОЙ РАСЧЕТ И ДИНАМИКА МАНИПУЛЯЦИОННЫХ МЕХАНИЗМОВ
Учебное пособие
Воронеж 2004
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
В.А. Рябцев В.А. Трубецкой
СИЛОВОЙ РАСЧЕТ И ДИНАМИКА МАНИПУЛЯЦИОННЫХ МЕХАНИЗМОВ
Утверждено Редакционно – издательским советом университета в качестве учебного пособия
ВОРОНЕЖ 2004

УДК 539.3/6
Рябцев В.А., Трубецкой В.А. Силовой расчет и динамика манипуляционных механизмов: Учеб. пособие / Воронеж: Воронеж. гос. техн. ун – т, 2004. 94с.
Учебное пособие включает материал силовому расчету, приведенным характеристикам, динамике и схватам манипуляционных механизмов. Издание соответствует рабочей программе дисциплины «Проектирование роботов и РТС» и предназначено для студентов специальности 210300 «Роботы и робототехнические системы» дневной и вечерней форм обучения.
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD 97 и содержится в каталоге
«PosobMM2».
Ил. 17. Библиогр.: 7 назв.
Научный редактор д- р техн. наук, проф. А.И. Шиянов
Рецензенты: кафедра теоретической механики Воронежской технологической академии (заведующий кафедрой
д-р техн. наук, проф. В. Н. Колодежнов); канд. техн. наук, доц. Ю.С. Слепокуров
Рябцев В. А., Трубецкой В.А., 2004
Оформление. Воронежский государственный технический университет, 2004
ВВЕДЕНИЕ
Предлагаемое учебное пособие включает материал по статике и динамике манипуляционных механизмов, относящийся к разделу «Манипуляционные механизмы» курса «Проектирование роботов и РТС». Основная часть этого материала основана на идеях и подходах, принятых в [5], где они изложены в кратком справочном виде, практически не доступном для студентов. Другие подходы к построению основных соотношений, приводят к трудно алгоритмизируемым соотношениям, использование которых при решении практических задач приводит к ошибкам либо на стадии аналитического решения задачи, либо при программировании вычислений на ЭВМ.
При работе над пособием студент обязан сначала хорошо освоить аппарат теории матриц и символику обозначений, принятую при изложении материала, а также материал учебного пособия [7].
В пособии рисунки нумеруются так, что первая цифра номера рисунка совпадает с номером раздела, к которому относится рисунок. Например, рис. 3.5 указывает на пятый рисунок из третьего раздела.
Формулы нумеруются так, что первая цифра номера рисунка совпадает с номером подраздела, к которому относится формула. Ссылки на эту формулу могут выглядеть различно в зависимости от места, из которого производится ссылка. Например, формула 5 указывает на пятую формулу из текущего подраздела, формула (2.5) указывает на пятую формулу из второго подраздела, формула (3.2.5) указывает на пятую формулу из второго подраздела третьего раздела.
3
1. СИЛОВОЙ АНАЛИЗ МАНИПУЛЯЦИОННЫХ МЕХАНИЗМОВ
1.1. Задачи силового анализа ММ
На звенья ММ и их элементы действуют силы и моменты различной природы, обусловленные полем сил тяжести, трением, движением звеньев и сопротивлением ему окружающей среды, выполняемыми производственными операциями, приводными устройствами и другими причинами. Далее силы и моменты, действующие на звенья и приводные устройства манипулятора, называются нагрузками.
Обобщенные кинематические характеристики ММ включают в себя обобщенные координаты [7]
qˆ ={q0 , q1 , …qn}T,
обобщенные скорости
qˆ ={ q0 , q1 , … qn }T
и обобщенные ускорения его звеньев
qˆ ={ q0 , q1 , … qn }.
Всиловом анализе ММ решаются следующие задачи:
1.Определение нагрузок на звенья, если они не заданы;
2.Определение реакций в кинематических парах и нагрузок на приводные устройства, при которых звенья ММ совершают заданные движения.
При решении задач силового анализа кинематические характеристики, а также обобщенные характеристики ММ, считаются известными и используется принцип Даламбера: произвольно движущееся звено механизма можно считать находящимся в равновесии и описывать это равновесие уравнениями статики, если к действующим на звено нагрузкам добавить инерционные нагрузки.
74
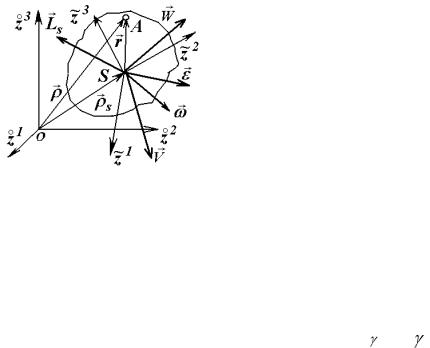
Уравнения равновесия звена, записанные с учетом инерционных нагрузок, называются уравнениями кинетостатики.
Силовой анализ ММ имеет очень важное значение, т.к. дает информацию для расчетов прочности звеньев и их элементов, долговечности подвижных соединений, расчетов затрат энергии на функционирование механизма, деформаций звеньев и точности позиционирования схвата.
1.2. Силы инерции и их моменты
Манипуляторы являются достаточно динамичными механизмами и поэтому инерционные нагрузки на их звенья в общем случае оказываются
|
весьма значительными, срав- |
|
нимыми с прочими нагрузками |
|
на звенья ММ. Во многих слу- |
Рис. 1.1. |
чаях они превышают другие |
|
|
|
нагрузки, действующие на ме- |
ханизм.
Пусть с звеном, совершающим сложное пространственное
~
движение, связана центральная система координат Z , а систе-
ма координат |
o |
является инерциальной системой |
отсчета |
Z |
|||
(рис.5.1). Частицу звена с объемом dV и массой dm = |
dV ( - |
||
плотность материала звена в точке А) можно считать материальной точкой. Ускорение точки А
|
e |
r |
k |
e |
, |
W |
'=W |
+W |
+W |
=W |
|
|
|
75 |
|
|
|
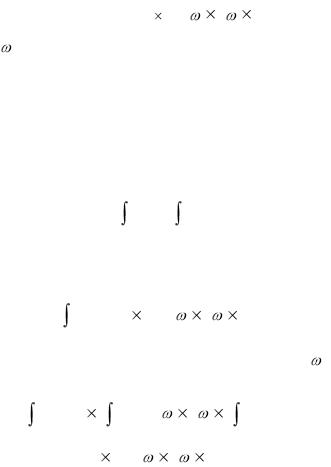
поскольку относительного движения у точки А нет. Если W - ускорение полюса, то
|
|
|
|
|
|
( |
r ), |
||
|
W |
'=W e |
=W |
+ ε |
r + |
||||
- абсолютные угловые ускорение и скорость звена. |
|||||||||
где ε и |
|||||||||
Согласно принципу Даламбера материальная точка А будет находиться в равновесии, если к действующим на нее внешним силам добавить силу инерции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dF = - dmW |
' . |
|
|
|
||
Действующая на все звено суммарная сила инерции |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
= dF = - |
γ W 'dV |
|
|
|
||
|
|
|
|
v |
v |
|
|
|
|
|
называется главным вектором сил инерции звена. |
|
|||||||||
По определению |
|
|
|
|
|
|
|
|||
|
|
|
|
r +( |
|
( |
r ))]dV. |
|
||
|
|
F =- |
γ [W |
+ ε |
|
|||||
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одина- |
||
Поскольку для всех точек звена векторы W , |
ε и |
|||||||||
ковы, |
|
|
|
|
|
|
|
|
|
|
|
|
|
γ r dV- |
|
( |
γ r dV)=- |
|
|||
F |
= -W |
γ dV- ε |
|
W m – |
||||||
|
|
v |
|
v |
|
|
v |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
- ε |
S s - |
S s ). |
|
|
|
||
Если полюс совпадает с центром масс S, то S s =0 и
|
|
|
F |
= - mW , |
(2.1) |
то есть главный вектор сил инерции, действующих на звено,
равен произведению массы m звена на ускорение W центра
76

масс звена, направлен противоположно этому ускорению и приложен в центре масс звена.
Для звена с номером i
Fi = -mi Wi ,
где Wi - ускорение центра масс звена i.
Согласно (4.5.9) [7],
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
|
|
|
|
|
Wi |
= |
j 1 |
ij q j + |
|
i +W0 . |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
aij = - mi |
ij , |
a0 j |
= - mi |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
(2.2) |
|
|
|
|
|
Fi = |
|
aij q j + a0i - mi W0 . |
||||||||||
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
В некоторой системе координат Zi , связанной с звеном i, |
|||||||||||||||
(2) принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ˆ |
|
ˆ |
|
|
|
|
|
|
|
(2.3) |
|
|
|
|
|
|
Fi = -mi Wi , |
|
|
|
|
|
|
||||
где |
ˆ |
k |
}, |
ˆ |
|
k |
} |
(k = 1,2,3) – матрицы-столбцы, оп- |
||||||||
Fi ={ Fi |
|
Wi ={Wi |
||||||||||||||
ределенные проекциями векторов |
|
и |
|
|
на оси системы ко- |
|||||||||||
Fi |
Wi |
|||||||||||||||
ординат Zi, связанной с звеном i . |
|
|
|
|
|
|
|
|||||||||
|
В той же системе координат Zi (2) приобретает вид |
|
||||||||||||||
|
|
|
|
ˆ |
|
i |
|
|
+ aˆ |
|
|
|
ˆ |
|
, |
(2.4) |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|||||
|
|
|
|
F = |
|
|
oi |
-m W |
||||||||
|
|
|
|
|
i |
|
aij q j |
|
|
i |
|
oi |
|
|
||
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
77
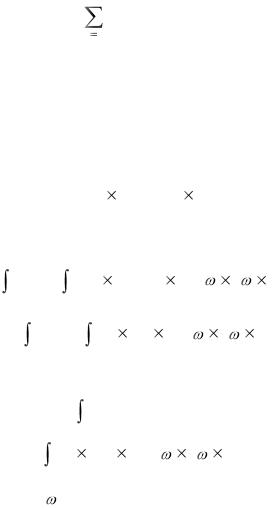
где |
aˆ ij , aˆoi , |
ˆ |
|
|
|
|
|
|
|
|
|
|||
Woi - трехмерные матрицы, определенные в сис- |
||||||||||||||
теме координат Zi. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
В неподвижной системе отсчета Z |
|
|
|||||||||||
|
|
|
|
|
|
o |
|
|
i |
o |
|
o |
o |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ˆ |
|
|
|
ˆ |
|
ˆ |
ˆ |
|
|
|
|
|
|
|
F i = |
|
|
a |
-mi Wo , |
(2.5) |
|||
|
|
|
|
|
|
j |
|
1 |
ij q j + aoi |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
o |
|
o |
|
|
o |
|
|
|
|
|
|
|
|
где |
ˆ |
, |
|
, |
ˆ |
|
- |
трехмерные матрицы, определенные в |
||||||
ˆ |
|
W |
||||||||||||
|
a ij |
|
aoi |
|
|
o |
|
|
|
|
|
|
|
|
o
системе Z .
Элементарная сила инерции dF создает относительно точки S элементарный момент
|
|
|
|
dM = r |
dF = -( r |
W |
')dV. |
Главный вектор – момент сил инерции относительно цен-
тра масс звена S определяется выражением
|
|
|
{ r |
|
|
r + |
( |
|
r )]}dV= |
M = dM = - γ |
[W + |
ε |
|
||||||
v |
|
v |
|
|
|
|
|
|
|
|
γ r dV- |
γ r |
|
r + |
( |
r )]dV. |
|||
=W |
[ ε |
||||||||
|
v |
|
v |
|
|
|
|
|
|
Поскольку начало отсчета системы координат Z находится |
|||||||||
|
|
|
|
|
|
|
|
|
|
в центре масс звена, |
γ r dV= Ss =0 и |
|
|
|
|||||
|
|
v |
|
|
|
|
|
|
|
|
|
γ r |
[( ε |
r )+ |
( |
r )]dV, |
|
||
M = - |
(2.6) |
||||||||
|
|
v |
|
|
|
|
|
|
|
|
и |
r удобно определять в связанной с зве- |
|||||||
Векторы |
ε , |
||||||||
|
~ |
|
|
|
|
|
|
|
|
ном системе Z матрицами |
|
|
|
|
|
||||
|
|
|
|
78 |
|
|
|
|
|

~ |
={ |
~k |
~ |
~k |
}, |
~ |
~ k |
} (k=1,2,3) |
εˆ |
|
}, ˆ ={ |
|
rˆ |
={ r |
Согласно Приложению [7], векторному выражению (6) соответствует выражение
|
~ |
~ |
~ |
|
~ |
~ |
|
~ |
~ |
~ |
|
|
ˆ |
|
|
||||||||
|
M =( |
γ D( rˆ )D( rˆ )dV) |
εˆ +D( ˆ |
)( |
γ D( rˆ )D( rˆ |
)dV) ˆ . |
|||||
|
|
v |
|
|
|
|
|
|
v |
|
|
|
|
~ |
|
|
~ |
~ |
|
|
матрица |
инерционных |
|
|
Поскольку J =- |
γ D( rˆ |
)D( rˆ )dV- |
||||||||
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
характеристик звена в системе координат Z , |
|
|
|||||||||
|
|
~ |
|
~ |
~ |
~ |
~ |
~ |
|
|
|
|
|
ˆ |
|
|
|
(2.7) |
|||||
|
|
M |
= - J |
εˆ -D( ˆ ) J |
ˆ . |
|
|||||
|
В главной, связанной со звеном, системе Z |
|
|
||||||||
|
|
ˆ |
= -J εˆ -D( ˆ )J ˆ |
|
|
|
(2.8) |
||||
|
|
M |
|
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
М1= -J11 |
1 +(J22–J33) |
2 |
3, |
|
|
||||
|
|
М2= -J22 |
2 +(J33–J11) |
3 |
1, |
|
(2.9) |
||||
|
|
М3= -J33 |
3 +(J11–J22) |
1 |
2. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
o |
|
Проекции вектора |
M на оси неподвижной системы Z |
|||||||||
определяется матрицей |
|
|
|
|
|
|
|
||||
|
|
|
|
|
o |
o |
ˆ |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
M = K |
M , |
|
|
|
||
|
o |
|
|
|
|
|
|
|
o |
|
|
где |
K - матрица преобразования Z |
|
Z . |
|
|
||||||
|
С учетом (8) |
|
|
|
|
|
|
|
|
|
|
|
|
o |
o |
ˆ |
|
o |
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
M = K |
M = - K (J εˆ +D( ˆ )J ˆ ). |
|
|
||||||
|
|
|
|
|
|
79 |
|
|
|
|
|
