
2485
.pdf
1.7. Применение статистики Бозе-Эйнштейна к фононам. Теплоемкость кристаллической решетки
Фононы, имеющие целочисленный спин, подчиняются статистике Бозе-Эйнштейна.
Фононы могут испускаться и поглощаться, при этом число их не сохраняется, а меняется от температуры кристалла. В зависимости от степени возбуждения нормальных колебаний испускается то или иное число одинаковых фононов. Следовательно, химический потенциал фононного газа равен нулю (µ=0).
С учетом этого, функция распределения Бозе-Эйнштейна для фононов примет вид
|
|
|
1 |
|
|
|
|||
f (E) e |
1 . |
|
||
kT |
(1.29) |
|||
|
|
|
|
|
|
|
|
|
|
При Т=0 кристалл находится в основном состоянии, характеризующимся полным отсутствием фононов. При достаточно низкой температуре, когда kT<<ћω, вероятность возбуждения фонона с частотой ω мала. При kT≈ћω среднее число фононов с частотой ω становится примерно равным единице. Это означает, что при данной температуре в кристалле возбуждаются все фононы с частотами меньшими и равными ω, а фононы с энергией ћω>kT практически не возбуждаются. По достижению характеристической температуры Дебая (ћωD≈kΘ) возбуждаются все высокочастотные фононы вплоть до максимальной частоты ωD.
Согласно определению, функция распределения выражает среднее число фононов, обладающих энергией ћω. Поэтому, умножая (1.29) на ћω, получим среднюю энергию Енк возбужденного нормального колебания, имеющего частоту ω:
Eнк e
|
|
1 |
|
kT |
1 |
. |
(1.30) |
|
|
|
|
|
|
|
|
20

Внутренняя энергия кристалла U складывается из энергии всех нормальных колебаний решетки, т.е. может рассматриваться
как энергия фононного газа и определяется выражением |
|
|||
|
D |
|
|
|
U |
|
E |
нк g( )d . |
(1.31) |
|
0 |
|
|
|
Теплоемкость кристаллической решетки при постоянном объеме выражает количество энергии, поглощаемой решеткой
при нагревании на 1К и находится дифференцированием |
|
||
C |
dU |
, |
(1.32) |
|
|||
V |
dT |
|
|
|
|
|
|
где внутренняя энергия U определяется выражением (1.31).
Не прибегая к строгим расчетам, проанализируем качественно зависимость теплоемкости кристаллической решетки от температуры.
В области низких температур (Τ<<Θ) энергия кристалла с повышением температуры увеличивается вследствие действия двух механизмов:
1)роста средней энергии каждого нормального колебания из-за повышения степени его возбуждения, т.е. роста числа тождественных фононов;
2)роста числа новых возбужденных нормальных колебаний решетки, т.е. увеличения числа более высокочастотных фононов.
Вцелом, с повышением температуры энергия решетки
растет пропорционально Т4, а теплоёмкость – пропорционально
Τ3, т.е.
CV ~ T3. |
(1.33) |
Соотношение (1.33) выражает закон Дебая, хорошо выполняющийся в области низких температур.
В области высоких температур (Τ>Θ) возбуждаются все нормальные колебания кристаллической решетки (весь спектр фононов) и дальнейшее повышение температуры не может
21

привести к увеличению их числа. Поэтому в данной области температур второй механизм роста энергии с повышением температуры выключается полностью. Изменение энергии твердого тела может происходить только за счет повышения степени возбуждения нормальных колебаний, приводящего к увеличению их средней энергии. При этих температурах преимущественно возбуждаются фононы максимальной частоты. Так как Eнк ~T, а число нормальных колебаний Z=const,
то изменение энергии тела с ростом температуры должно происходить пропорционально температуре (U~T), a теплоемкость тела не должна зависеть от Т
C |
dU |
const . |
(1.34) |
V dT
Соотношение (1.34) согласуется с законом Дюлонга и Пти, ранее установленным экспериментально: удельная теплоемкость всех твердых тел при достаточно высоких температурах есть величина постоянная, не зависящая от температуры, и составляет около 25Дж·моль-1.К-1:
CV=3R
где R=8,314 Дж·моль-1.К-1 – универсальная газовая постоянная.
25
20
15
10
5
|
|
|
|
|
|
|
|
|
|
|
T / |
0 |
|
0,2 |
|
0,4 |
|
0,6 |
|
0,8 |
|
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.5
22

Между областями низких и высоких температур лежит достаточно широкая область так называемых средних температур, в которой происходит постепенный переход от закона Дебая к закону Дюлонга и Пти. Расчетная кривая зависимости теплоемкости твердых тел от относительной температуры T / представлена на рис.1.5. Данная кривая хорошо согласуется с экспериментальными результатами для целого ряда веществ.
Зная температурную зависимость энергии решетки, можно качественно установить зависимость концентрации фононного газа от температуры.
В области низких температур U~T4, а энергия фононаkT ~ T , поэтому
|
|
nф ~ Т3 . |
|
|
|
(1.35) |
|||
В области высоких температур U~T, а энергия фонона |
|||||||||
достигает |
предельного |
значения |
D k , |
не зависящего |
от |
||||
температуры, поэтому |
|
|
|
|
|
|
|
||
|
|
nФ~Т. |
|
|
|
(1.36) |
|||
1.8. Применение статистики Ферми-Дирака к электронному |
|||||||||
|
|
газу в металлах |
|
|
|
|
|||
Электрические, тепловые, оптические и некоторые другие |
|||||||||
свойства металлов определяются состоянием свободных |
|||||||||
электронов в них. Поэтому основной задачей квантовой теории |
|||||||||
металлов является выяснение закономерностей в распределении |
|||||||||
0 |
0 |
свободных электронов по энергиям. |
|
||||||
Согласно |
модели |
свободных |
|||||||
|
|
||||||||
N / 2 |
Eф |
электронов |
валентные |
электроны |
|||||
|
могут почти |
свободно перемещаться |
|||||||
|
|
||||||||
|
Eф |
по всему объему, подобно молекулам |
|||||||
3 |
идеального газа. |
Электронный газ |
в |
||||||
|
|||||||||
2 |
|
металле |
является |
вырожденным |
и |
||||
1 |
|
||||||||
Рис. 1.6 |
подчиняется |
статистике |
Ферми- |
||||||
|
|
|
|
|
|
|
|||
|
|
23 |
|
|
|
|
|
|
|

|
f (E) |
|
dN |
|
|
|
|
dE |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
Eф |
E |
0 |
Eф |
E |
|
Рис. 1.7 |
|
|
Рис. 1.8 |
|
Дирака. Рассмотрим, прежде всего, его поведение при Т=0 К. Электрон в металле находится в потенциальной яме,
образованной его поверхностью, выход из которой требует совершения работы по преодолению сил связи электронов с ионами кристаллической решетки (рис. 1.6). Спектр разрешенных отрицательных значений энергии электронов в потенциальном поле решетки, связанный с их волновым характером движений, дискретен. Горизонтальными линиями на представленной схеме показаны энергетические уровни, которые могут занимать электроны. В соответствии с принципом Паули, на каждом таком уровне размещаются по два электрона с противоположными спинами. Если число электронов Ν, то последним занятым уровнем при Т=0К окажется уровень Ν/2. Этот уровень называется уровнем Ферми. Он соответствует максимальной кинетической энергии Еф, которой может обладать электрон в металле при абсолютном нуле. Ее называют энергией Ферми.
Учитывая, что в этих условиях химический потенциал электронного газа, отсчитанный от дна потенциальной ямы, равен энергии Ферми μ = Еф, функцию распределение ФермиДирака можно записать в виде
fф (E) e
E Eф |
1 |
|
|
|
|
|
|
kT |
|
||
1 . |
(1.37) |
||
|
|||
|
|
|
|
|
|
|
24

Данная функция, определяющая вероятность заполнения электроном энергетического уровня с энергией Ε, при Т=0К принимает следующие значения:
fф (E) 1 для E<Eф и fф (E) 0 для E>Eф . (1.38)
Ее график, имеющий вид ступеньки, представлен на рис.1.7. Из графика видно, что при Т=0К все состояния с энергией Е<Еф заняты электронами, а состояния с энергией
Е>Еф свободны.
Распределение электронов по энергиям описываются функцией (1.9), которая с учетом (1.8) и (1.38) приобретает вид:
dN |
|
4 V |
(2m)3 / 2 |
|
|
(1.39) |
|
EdE |
|||||
|
|
|||||
|
|
h3 |
|
|
|
|
График этой функции приведен на рис. 1.8, в котором |
||||||
область занятых состояний заштрихована. |
|
|||||
Получив, путем |
интегрирования выражения |
(1.39) в |
||||
пределах от 0 до Еф, полное число свободных электронов в металле
N |
8V |
E3 / 2 (2m)3 / 2 , |
(1.40) |
|||||
3h3 |
||||||||
|
|
ф |
|
|
|
|||
легко определить энергию Ферми |
|
|
|
|
|
|||
|
|
h2 |
|
3n 2 / 3 |
|
|||
Eф |
|
|
|
|
|
(1.41) |
||
|
|
|
||||||
|
|
2m |
8 |
|
||||
где n=N/V – концентрация электронного газа.
В соответствии с полученным выражением энергия Ферми зависит от концентрации валентных электронов. Приняв в качестве характерной величины n=5∙1028м-3, получим числовую оценку для энергии Ферми в металлах: Еф≈ 5эВ.
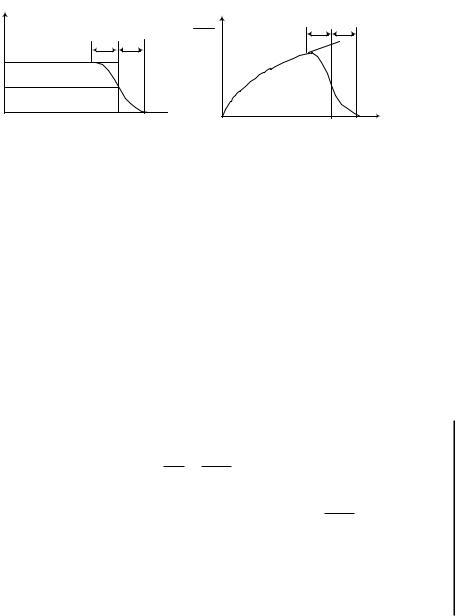
С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни. Этот процесс вызывает размытие функции распределения f(Ε) на глубину kТ, соответствующую энергии теплового движения (рис.1.9).
25
fф (E) |
|
|
dN |
kT kT |
|
|
|
|
|
||
|
kT kT |
|
dE |
|
|
1 |
|
|
|
|
|
1/ 2 |
|
|
|
|
|
0 |
Еф |
Е |
0 |
Еф |
Е |
|
|||||
|
Рис. 1.9 |
|
|
Рис. 1.10 |
|
Чем выше температура, тем более существенному изменению подвергается функция распределения. Одновременно с этим искажается и кривая распределения электронов по энергиям (рис. 1.10). В соответствии с (1.30) при Е=Еф функция f(Ε)=1/2 при любой температуре T>0. Поэтому со статистической точки зрения уровень Ферми представляет собой энергетический уровень, вероятность заполнения которого равна 1/2.
Произведем приближенную оценку числа электронов, переходящих на уровни, расположенные выше Еф. Расстояния между соседними энергетическими уровнями
|
Eф |
|
2Eф |
. |
|
|
|||
|
N / 2 |
|
N |
|
Число уровней, находящихся в полосе термического возбуждения, определяется выражением
kT kTN ,
2Eф
а возможное число электронов в два раза больше, т.е. kTN .
Eф
Полагая, что за уровень Ферми переходит не более
половины этих электронов, получаем |
|
||
N ~ |
kTN |
. |
(1.42) |
|
|||
|
2Eф |
|
|
26

При комнатной температуре kТ~0,025эВ, Еф~5эВ, поэтому Ν/Ν<1%; при Т=1000К ∆N/N~1%. Таким образом, во всем диапазоне температур электронный газ в металле является вырожденным, а его распределение мало отличается от распределения при абсолютном нуле и химический потенциал μ совпадает с Eф.
Температура Ферми, определяемая выражением |
|
||
T |
Eф |
, |
(1.43) |
|
|||
ф |
k |
|
|
|
|
||
показывает, при какой температуре электронный газ в металле переходит в невырожденное состояние. Для металлов Тф~105К, т.е. столь высока, что ни один металл при таких температурах не может существовать в конденсированном состоянии.
Рассмотрим основные свойства вырожденного электронного газа.
Средняя энергия одного электрона при абсолютном нуле, рассчитанная по формуле (1.17) с учетом (1.8) и (1.38), определяется выражением
|
|
|
3 |
E . |
(1.44) |
0 |
|
||||
|
|
5 |
ф |
|
|
|
|
|
|
|
|
Поскольку энергия Ферми |
практически |
не зависит от |
|||
температуры, то и среднюю энергию электрона можно считать также независимой от температуры ( 0 ).
Максимальная и средняя квадратичная скорость электронов вычисляется по формулам
|
|
|
2Eф |
, |
|
|
|
2 |
. |
|
max |
m |
кв |
m |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Расчет по этим формулам дает значение ~106 м/с.
Таким образом, вырожденный электронный газ существенно отличается по своим свойствам от идеального невырожденного газа. В то время как для идеального газа средняя энергия частиц и их квадратичная скорость являются функцией температуры и при абсолютном нуле обращаются в
27

нуль, |
для |
вырожденного |
|
|
|
|
|
|
|||
электронного |
газа |
|
и |
кв |
|
E |
|
|
|
||
уже |
при |
Т=0 |
|
имеют |
|
|
|
|
Вырожденные |
Невырожденные |
|
|
|
|
|
|
состояния |
состояния |
|||||
|
|
|
|
|
|
|
|
|
|
||
большую |
величину |
и |
|
|
|
|
|
|
|||
практически |
не зависят от |
|
|
|
|
|
|
||||
температуры (рис.1.11). |
Это |
|
|
0 |
Tф |
T |
|||||
указывает на то, что энергия |
|
|
|||||||||
|
|
|
|
|
|
||||||
электронного газа в металле |
|
|
|
|
Рис. 1.11 |
|
|||||
имеет в подавляющей своей |
|
|
|
|
|
|
|||||
части нетермическую природу. |
|
|
|
|
|
|
|||||
|
Электронный газ не вносит заметного вклада в |
||||||||||
теплоемкость металлов. Этот факт объяснил в 1928 г. немецкий |
|||||||||||
физик Зоммерфельд. Согласно его теории металлов, физическая |
|||||||||||
малость теплоемкости вырожденного электронного газа |
|||||||||||
объясняется тем, что в теплоемкости участвуют не все |
|||||||||||
электроны, а лишь незначительная их доля, располагающаяся |
|||||||||||
непосредственно у уровня Ферми. Ранее проведенная оценка |
|||||||||||
показывает, что число таких электронов <1 %. Остальные |
|||||||||||
электроны, находящиеся в глубинных ячейках, теплоту не |
|||||||||||
поглощают, так как не могут перейти на более высокие уровни – |
|||||||||||
все состояния заняты. |
|
|
|
|
|
|
|
|
|||
|
Каждый электрон, подвергающийся термическому |
||||||||||
возбуждению, поглощает энергию порядка kT. Энергия, |
|||||||||||
поглощаемая всем электронным газом, заключенным в одном |
|||||||||||
моле металла, равна произведению kT на число электронов ∆N, |
|||||||||||
испытывающих термическое возбуждение: |
|
||||||||||
|
|
|
E ~ kT N ~ N |
A |
kT kT . |
(1.45) |
|||||
|
|
|
|
e |
|
|
|
|
Eф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, молярная теплоемкость электронного газа равна |
|||||||||||
|
|
|
|
C |
dEe |
~ N |
|
k kT |
(1.46) |
||
|
|
|
|
V |
dT |
|
A |
|
|
Eф |
|
|
Если бы электронный газ был обычным классическим, то |
||||||||||
его молярная теплоемкость была бы равна |
|
||||||||||
|
|
|
|
|
|
28 |
|
|
|
|
|

Cкл |
3 |
N |
|
k |
3 |
R |
(1.47) |
||||
|
|
A |
|
||||||||
V |
2 |
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
||||
Сравнивая (1.46) и (1.47), найдем |
|
||||||||||
|
CV |
|
~ |
kT |
~ 0,01 |
(1.48) |
|||||
|
C кл |
|
E |
ф |
|||||||
|
|
|
|
|
|
|
|
||||
|
V |
|
|
|
|
|
|
|
|
|
|
Таким образом, теплоемкость электронного газа незначительна по сравнению с теплоемкостью решетки и теплоемкость металла практически равна теплоемкости его решетки.
На рис. 1.12 показаны |
|
Дж |
||
графики |
температурной |
СV , |
||
|
||||
моль К |
||||
зависимости |
теплоемкости |
1,6 |
|
|
|
|
|
||
решетки (сплошной линией) |
|
|
||
иэлектронного газа 1,2
(пунктирная |
линия). |
Как |
0,8 |
|
|
Сэл ~ T |
|
|
|
|
||||||
видно из |
рисунка, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
только вблизи |
абсолютного |
0,4 |
|
|
|
|
|
|
|
|
Среш |
~ T |
3 |
|
||
нуля |
теплоемкость |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
электронного |
газа |
может |
|
0 |
|
|
10 |
20 |
30 |
40 T,K |
||||||
приобрести |
основное |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Рис. 1.12 |
|
|
|
||||||
значение благодаря тому, что |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
с понижением температуры теплоемкость решетки падает ~Т3 (см. 1.33), а теплоемкость электронного газа согласно (1.46) падает медленнее (~Т).
1.9. Электропроводность металлов
В классической электронной теории (теория ДрудеЛоренца) электроны проводимости рассматриваются как идеальный газ. В отсутствие электрического поля они хаотически движутся и сталкиваются с ионами металлов, которые в свою очередь, совершают тепловые колебания около положения равновесия. При приложении электрического поля электроны проводимости приобретают некоторую скорость
29
