Высшая математика. Функции нескольких переменных: практикум. Пантелеев И.Н

1

9

. Наименьшее

значение

функции

равно

zmax 2;

=

4

2

zmin = −

1 .

Наименьшее значение функция принимает в двух

4

точках

1

;0

и

1

,1 .

2

2

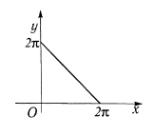
б) Заданная область представляет треугольник (рис. 1.1).

Найдем стационарные точки: z'

= 2x +1 , z'

= 6 y −1 , x

= − 1 ,

x

y

0

2

на отрезке 0 ≤ y ≤1.

Находим zy = 6 y −1 ,

y =

1 ,

z''yy = 6 > 0 . Точка

y = 1 -

6

6

точка минимума;

1

23

.

На границе

отрезка

zmin 1;

=

6

12

z(1, 0) = 2,

z(1,1) = 4 .

При

y =1 имеем z = x2 + x + 2 .

Исследуем эту функцию

на отрезке 0 ≤ x ≤1.

отрезка: z(0,1) = 2

и z(1,1) = 4 .

При

x + y =1

имеем

z = 4y2 −4y +2 .

Исследуем

эту

функцию

на отрезке

0 ≤ y ≤1.

Находим

z'y =8y −4 ,

y =

1 ,

1

1

1

2

''

. Точка

y =

-

точка минимума

.

В

zyy = 8 > 0

2

zmin

;

=1

2

2

граничных точках функция равна z(0,1) = 2 , z(1, 0) = 2 .

Сравнивая

значения

функции на

границе

заданной

области,

находим

наименьшее

значение

1

1

и

zmin

;

=1

2

2

dz

= cos x −cos(x + y) = 0 ,

dz

= cos y −cos(x + y) = 0 .

dx

dy

Из

решения

системы

имеем:

cos x −cos y = 0 ,

sin

x + y

sin

x − y

= 0 ,

y = ±x + 2kπ . Поскольку x изменяется в

2

2

промежутке 0 < x < 2π , то

достаточно рассмотреть случай

y = x . Функция при

y = x

примет вид

z = 2sin x −sin 2x .

Откуда zx'

= 2 cos x −2 cos 2x ,

cos x −cos 2x = 0 ,

2x = ±x +2kπ .

Значение x = 2kπ

не

лежит внутри

области

и его не

следует рассматривать.

2 kπ и при k =1

Следовательно, y = x =

это будет точка

2π

2π

3

x

=

,

y

=

. Так

как точка

(x , y )

- единственная

0

0

3

3

0

0

стационарная точка в области и функция в ней равна z =

3 3

,

2

то на границе, т. е. при

x = 0, y = 0, x + y = 2π

функция равна

нулю z = 0 .

В точке (x0 , y0 )

функция принимает наибольшее

значение, а на границе наименьшее.

10.2. На плоскости

Oxy найти точку

M (x, y) , сумма

квадратов

расстояний

которой

от

трех

прямых:

x = 0, y = 0, x − y +1 = 0 была бы наименьшей.

расстояний до прямых x = 0, y = 0 соответственно равны x2

и

y2 , а квадрат расстояния от точки до прямой

x − y +1 = 0

по

формуле d =

Ax + By +C

равен

x − y +1

2 , то сумма

A2 + B2

2

квадратов расстояний будет u = x2 + y2 +

1 (x − y +1)2 .

2

du

= 3x − y +1 = 0 ,

du

= −x +3y −1 = 0 . Отсюда единственная

dx

dy

стационарная точка M (x, y)

имеет координаты x = −

1

,

y =

1 .

4

4

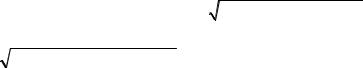
Так как

A =

d 2u

= 3

,

B =

d 2u

= −1,

C =

d 2u

= 3

и

dx

2

dxdy

dy2

D = AC − B

2

= 8

> 0

при

A > 0 (C > 0) , то в точке

M

−

1

,

1

4

4

функция u суммы квадратов расстояний минимальна.

10.3.

Из

всех

треугольников

данного

периметра

2 p

тогда по

формуле

Герона S = p( p − x)( p − y)( p − z)

или,

учитывая,

что

x + y + z = 2 p ,

будем

иметь

Чтобы найти наибольшее значение площади, достаточно

найти

наибольшее

значение

подкоренной

функции

u = ( p − x)( p − y)(x + y − p) .

Вычисляем производные и приравниваем их нулю

du

= −( p − y)(x + y − p) +( p − y)( p − x) = 0 ,

dx

du

= −( p − x)(x + y − p) + ( p − x)( p − y) = 0 .

dy

Из решения системы уравнений находим единственную

стационарную

точку

x = y = z =

2 p

.

Находим

вторые

3

производные

в

этой

точке:

A =

d 2u

= −

2 p

,

B

=

d 2u

=

p

,

dx2

3

dxdy

3

C =

d 2u

= −

2 p

.

dy2

3

Поскольку

D = AC − B2

=

p2

> 0 и

A < 0

(C < 0) ,

то

3

xyzt = a . Представляя

t в

виде t =

a

и подставляя

это

xyz

выражение в сумму,

будем

иметь

S = x + y + z +

a

, т.

е.

xyz

при условии, что переменные

x, y в окрестности этой точки

удовлетворяют

уравнению

связи ϕ(x, y) = 0 ,

т. е.

f (M0 ) > f (M )

или f (M0 ) < f (M ) при ϕ(x, y) = 0 и M ≠ M0 .

Для отыскания условного экстремума составляют

функцию Лагранжа

u(x, y, λ) = f (x, y) +λϕ(x, y) ,

(1)

du

= df

+λ dϕ

= 0;

du

= df

+ λ dϕ

= 0

(2)

dx

dx

dx

dy

dy

dy

0

ϕx' (M0 )

ϕy' (M0 )

(3)

D = −

ϕ'

(M

0

)

u''

(M

0

, λ )

u''

(M

0

, λ )

x

xx

0

xy

0

ϕ'

(M

0

) u''

(M

0

, λ ) u''

(M

0

, λ )

y

xy

0

yy

0

Если D < 0 , то

функция

z = f (x, y)

имеет в

точке

M0 (x0 , y0 )

условный

максимум,

а если

D > 0

-

условный

минимум.

20.

Функция нескольких

независимых

переменных

z = z(x )

(i =1, 2,..., n)

в точке

M

0

(xo )

имеет

условный

i

i

экстремум, если в некоторой окрестности точки

M0 для всех

ее точек

xi , удовлетворяющих уравнениям связи

ϕk (xi ) = 0 ,

(k =1, 2,..., m; m < n) ,

выполняется

неравенство

f (M0 ) > f (M ) f (M0 ) < f (M ); (M0 ≠ M ) .

Функция Лагранжа имеет вид

m

u(xi , λk ) = z(xi ) + ∑λkϕk (xi ) ,

(4)

k =1

где λk (k =1, 2,..., m)

- множители Лагранжа, причем их число

du

= 0

(i =1, 2,...n);

dxi

(M ) = 0

(k =1, 2,...m)

ϕk

Решая эту систему относительно неизвестных, находим

λ0

и координаты точки x0 , в которой возможен условный

k

i

экстремум.

Достаточные условия условного экстремума:

1)

если второй дифференциал

d 2u(x0

, λ0

, dx ) < 0 ,

i

k

i

при условии, что dxi удовлетворяет уравнениям

n

dϕ

k

(x0 )

∑

i

dx = 0 (k =1, 2,..., m)

(5)

dxi

i=1

n

При ∑dxi2

≠ 0 ,

то функция z = z(xi )

в точке

M0 (xio )

а) z = x +3y

при

x2 + y2 =10; б) u = x − 2 y + 2z при

x2 + y2 + z2 = 9; в)

u = xyz

при x + y + z = 5, xy + yz + xz = 8 .

Составим

функцию

Лагранжа

u(x, y, z) = x +3y +λ(x2 + y2 −10)

и

найдем

частные

производные: du

1+ 2λx;

du

= 3 + 2λy . Необходимые условия

dx

dy

Поскольку

d 2u

= 2λ ,

d 2u

= 0 ,

d 2u

= 2λ ,

то

dx2

dxdy

dy2

d 2u = 2λ(dx2 +dy2 ) .

При λ = −

1 ,

d 2u < 0 ,

следовательно,

2

функция имеет в точке M1(1,3)

условный максимум zmax =10 .

При λ = 1 , d 2u > 0 ,

следовательно,

функция имеет в точке

2

в

точке

M1 :

ϕ(x, y) = x2 + y2 −10 ,

ϕx' (M1 ) = 2 , ϕy' (M1 ) = 6 ,

u''

(M

, λ ) = −1

, u''

(M

, λ ) = 0

, u''

(M

, λ ) = −1

xx

1

1

xy

1

1

yy

1

1

D = −

0

2

6

= −40 < 0 ,

2

−1 0

6

0

−1

D = −

0

−2

−6

= 40 > 0 ,

−2 1 0

−6

0

1

т. е. функция в точке M2

имеет условный минимум.

б) Функция трех независимых переменных. Составим

функцию Лагранжа

w = x −2y +2z +λ(x2 + y2 + z2 −9)

и найдем частные производные

dw

=1+ 2λx ,

dw

= −2 + 2λx ,

dw

= 2 + 2λz .

dx

dy

dz

Запишем

необходимые

условия

существования

условного экстремума

1+2λx = 0, 1−2λy = 0,

1+2λz = 0, x2

+ y2 + z2 −9 = 0.

Из решения этой системы имеем

λ = 1

, x = −1,

y = 2

,

z = −2 ,

1

2

1

1

1

1 , x =1

λ = −

,

y = −2

,

z

2

= 2 .

2

2

2

2

Вычислим вторые производные

d 2 w

=

2λ ,

d 2 w

= 2λ ,

d 2 w

= 2λ ,

dx2

dy2

dz2

d

2w

=

d 2w

=

d 2w

= 0

dxdy

dxdz

dydz

и найдем второй дифференциал в первой критической

точке

2

1

=1 > 0 .

Поскольку

знак второго

d

w −1, 2, −2,

2

точке

2

1

отрицательный, следовательно,

d

w 1,

−2, 2, −

= −1 < 0

2

dw

= xy +λ +λ y +λ x = 0 ,

dz

1

2

2

x + y + z = 5 , xy + yz + xz = 8 .

Из

решения

этой

системы

уравнений

находим

критические

точки:

M1(2, 2,1) ,

4

4

4

,

M3 (2,1, 2) ,

M 2

,

,

3

3

4

7

4

7

4

4

3

M 4

,

,

,

M5 (1, 2, 2) , M6

,

,

.

3

3

3

3

3

3

Вычисляем вторые частные производные

d 2 w

=

d 2 w

=

d 2w

= 0 ,

dx2

dy2

dz2

d 2w

= z +λ ,

d

2 w

= x +λ ,

d 2 w

= y + λ

dxdy

dydz

dxdz

2

2

2

точках. В точке

M

1

d 2 w(2, 2,1, λ

= −1) = 4 > 0 функция имеет

2

условный

минимум

umin = 4 .

В

точке

M2

d 2 w( 4

, 4

, 7

, λ = − 7) = −4 < 0

функция

имеет условный

3

3

3

2

3

максимум

umax = 4

4

.

Аналогично

вычисляется

знак

второго

27