
Алгебра: курс лекций часть 3. Майорова С.П., Завгородний М.Г
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
С.П. Майорова М.Г. Завгородний
АЛГЕБРА: КУРС ЛЕКЦИЙ Часть 3
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2011
3
УДК 512.8
Майорова С.П. Алгебра: курс лекций: учеб. пособие / С.П. Майорова, М.Г. Завгородний. Воронеж: ФГБОУ ВПО «Воронежский государственный технический университет», 2011. Ч. 3. 144 с.
В учебном пособии содержится изложение теоретического материала по разделам: основы теории групп, конечные абелевы группы, кольца и поля курсов «Алгебра» и «Алгебра и геометрия». Приведены контрольные вопросы по всем темам и задания к типовым расчетам. Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлению подготовки (специальности) 090301 «Компьютерная безопасность» и 090303 «Информационная безопасность автоматизированных систем», дисциплинам «Алгебра» и «Алгебра и геометрия».
Пособие предназначено для студентов второго курса радиотехнического факультета очной формы обучения.
Учебное пособие подготовлено в электронном виде в текстовом редакторе MS Word и содержится в файле Алгебра-3.pdf.
Библиогр.: 7 назв.
Рецензенты: кафедра программного обеспечения и администрирования информационных систем Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф.
М.А. Артемов); д-р физ.-мат. наук, проф. М.И. Каменский
©Майорова С.П., Завгородний М.Г., 2011
©Оформление. ФГБОУ ВПО «Воронежский государственный технический университет», 2011
ВВЕДЕНИЕ
Развитие компьютерных и информационных технологий требует все большего внимания к вопросам информационной безопасности. Активно развиваются криптографические методы защиты информации, которые, в свою очередь, опираются на ряд алгебраических структур. Широко используются все разделы алгебры при изучении общетехнических
испециальных дисциплин, определяемых Федеральным государственным образовательным стандартом высшего профессионального образования по направлению подготовки (специальности) 090301 «Компьютерная безопасность» и 090303 «Информационная безопасность автоматизированных систем». Поэтому алгебра является одной из базовых дисциплин для указанных специальностей.
Данное пособие является составной частью комплекса учебных пособий по курсу «Алгебра» для студентов специальностей 090301 и 090303 радиотехнического факультета Воронежского государственного технического университета. В основу пособия положен теоретический материал по нескольким разделам курса: основы теории групп, конечные абелевы группы, кольца и поля, который излагается на лекциях, а также предлагается студентам для самостоятельного изучения. Большинство рассматриваемых в пособии понятий
ирезультатов иллюстрируется примерами. По всем темам приведены контрольные вопросы и задания на закрепление изложенного материала. В приложении приведены задания к типовым расчетам.
Данное пособие соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлению подготовки (специальности) 090301 «Компьютерная безопасность» и 090303 «Информационная безопасность автоматизированных систем» и предназначено для студентов второго курса.
3
§ 1. ОСНОВЫ ТЕОРИИ ГРУПП
Понятие группы является одним из основных понятий современной математики, широко используемым в различных областях науки и техники. В данном параграфе будут изложены основы общей теории групп.
1.1. Понятие группы. Конечные группы
Понятие группы ранее уже рассматривалось (см. часть 2 настоящего пособия). Напомним основные определения.
Определение. Множество G с заданной на нем бинарной операцией называется группой, если выполняются три условия:
1)операция ассоциативна, т.е. (a b) c =a (b c) для любых элементов a,b,c G;
2)существует нейтральный элемент e G такой, что
a e = e a = a для любого a G ;
3) для каждого элемента a G существует обратный
элемент a−1 G такой, что a a−1 = a−1 a = e . Определение. Если a b = b a для любых элементов
a,b G , то группа называется абелевой (или коммутатив-
ной).
Если групповая операция - это сложение, то группу называют аддитивной; если - это операция умножения, то группу называют мультипликативной. В дальнейшем в общих рассуждениях мы будем пользоваться, в основном, мульти-пликативной формой записи.
Введём новое понятие - понятие конечной группы. Определение. Группа G называется конечной, если
она состоит из конечного числа элементов. Число элементов группы называется ее порядком и обозначается | G |.
Так, если группа G состоит из n элементов, говорят, что порядок группы равен n и пишут | G |= n .
Определение. Группа, множество элементов которой бесконечно, называется бесконечной (или группой бесконеч-
ного порядка).
Отметим, что группа первого порядка содержит только один элемент, который обязательно должен быть её нейтральным элементом e . Поэтому группу первого порядка обычно называют единичной группой.
Приведем примеры групп.
Пример 1. Множество всех целых чисел с операцией сложения, т.е. ( , +) , является группой, её называют ад-
дитивной группой целых чисел. Эта группа абелева, ее ней-
тральным элементом является число 0; |
для каждого a |
|
определен противоположный элемент |
−a |
так, что |
a +(−a) = 0 . |
|
|
Отметим, что множество целых чисел с операцией умножения группой не является, так как относительно этой операции лишь два элемента (это 1 и -1) имеют обратные,
для всех остальных целых чисел элемент a−1 уже не является целым числом.
Пример 2. Рассмотрим кольцо K . Напомним определение кольца: множество K с двумя бинарными операциями "+" и " " называется кольцом, если:
1)(K, +) является абелевой группой;
2)(K, ) является полугруппой;
3)операции "+" и " " связаны законами дистрибутив-
ности.
Как видно из определения, (K, +) является группой, её
называют аддитивной группой кольца. Нейтральный элемент этой группы e = 0 является нулём кольца.
Полугруппа (K, ) называется мультипликативной полугруппой кольца. Отметим, что (K, ) в общем случае не яв-
4 |
5 |
ляется группой, так как в определении кольца не требуется, чтобы для любого элемента a K существовал обратный элемент a−1 K .
Пример 3. Рассмотрим поле P (напомним, что поле – это коммутативное кольцо с 1 ≠ 0 , в котором каждый нену-
левой элемент обратим). Через P* обозначим множество всех обратимых элементов поля P , т.е. P* = P \{0}. Тогда из
определения поля вытекает, что (P*, ) является группой; её называют мультипликативной группой поля.
Пример 4. Рассмотрим множество Ωn всех комплексных корней n -й степени из единицы относительно операции
умножения, |
|
т.е. |
|
Ωn ={ε0 ,ε1,...,εn−1} , |
где |
||||
εk = cos |
2πk |
+i sin |
2πk |
, |
k = |
|
|
яв- |
|
0, n −1 . Покажем, что (Ωn , ) |
|||||||||
n |
|
||||||||
|
|
n |
|
|
|
|
|||
ляется абелевой группой. |
|
||||||||
1) Умножение является бинарной операцией в Ωn . |
|||||||||
Действительно, пусть εk ,εp Ωn , т.е. εk n =1 и εpn =1. То- |
|||||||||
гда (εkεp )n =εknεpn =1. Это означает, что произведение εkεp
является корнем n-й степени из единицы, |
т.е. εkεp Ωn . |
Ассоциативность операции умножения в Ωn |
следует из ее |
ассоциативности в . |
|
2) В Ωn существует нейтральный элемент e =ε0 =1. |
|
3) Для любого числа εk Ωn обратное к нему число |
|
εk −1 также принадлежит Ωn . Действительно, пусть εk Ωn ,
т.е. εk n =1, тогда (εk −1)n = (1 εk )n =1
εk )n =1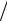 εk n =1. Поэтому εk −1 также является корнем n-й степени из единицы, т.е.
εk n =1. Поэтому εk −1 также является корнем n-й степени из единицы, т.е.
εk −1 Ωn .
Из свойств 1) - 3) вытекает, что (Ωn , ) является груп-
пой. Эта группа – абелева, так как умножение комплексных чисел коммутативно. Отметим, что (Ωn , ) является конеч-
ной группой и её порядок равен n .
Пример 5. Рассмотрим множество GLn (P) всех невырожденных квадратных матриц порядка n с элементами из
поля P , |
т.е. GLn (P) ={A Mn (P) : |
| A |≠ 0} . Покажем, что |
|
(GLn (P), ) является группой. Действительно: |
|||
1) |
Для любых |
матриц |
A, B GLn (P) имеем |
| AB |=| A | | B |≠ 0 , так как | A |≠ 0 и | B |≠ 0 . Следовательно, |
|||
матрица |
AB - невырождена. Причем, так как матрицы A и |
||
B имеют размер n ×n , |
то матрица |
AB также имеет размер |
|
n ×n , а значит AB GLn (P) , т.е. умножение является бинар-
ной операцией. Отметим, что эта операция ассоциативна, т.к. равенство ( AB)C = A(BC) верно для всех матриц.
2) Нейтральным элементом в GLn (P) является единич-
|
1 |
0 |
… |
0 |
|
|
|
|
ная матрица |
|
1 |
… |
0 |
|
, где 1 |
- единица поля P . |
|
E = 0 |
|
|||||||
|
… … |
|
… |
|
|
|||
|
|
0 |
… |
1 |
|
|
|
|
|
0 |
n×n |
|
|
||||
3) Для любой матрицы |
A GLn (P) существует обрат- |
|||||||
ный элемент |
A−1 (так как всякая невырожденная матрица |
|||||||
имеет обратную), причем A−1 |
также имеет размер n ×n и ее |
|||||||
определитель | A−1 |= |
1 |
≠ |
0 . Следовательно, A−1 GL (P) . |
|||||
|
|
|||||||
|
|
|
| A | |
|
|
|
|
n |
|
|
|
|
|
|
|
(GLn (P), ) является |
|
Из свойств 1) |
- 3) |
вытекает, что |
||||||
группой. Отметим, что эта группа не является абелевой, так как AB ≠ BA для любых матриц A, B GLn (P) . Рассмотрен-
6 |
7 |
ную группу (GLn (P), ) называют группой обратимых мат-
риц.
Важным примером конечной группы является группа подстановок. Ниже рассмотрим эту группу более подробно.
Контрольные вопросы и задания к п. 1.1
1.Сформулируйте определение группы.
2.Какая группа называется абелевой?
3.Какая группа называется конечной? Приведите пример конечной группы. Что называют порядком конечной группы?
4.Докажите, что если a2 = e для любого элемента a группы, то группа абелева.
5.Докажите, что множество ненулевых действительных чисел с операцией , заданной равенством a b = 5ab , явля-
ется группой. Найдите элемент, обратный к элементу
a= 3.
6.Выясните, образует ли группу множество положительных действительных чисел относительно операции , задан-
ной равенством: а) a b = ab , б) a b = a2b2 .
1.2.Группа подстановок (симметрическая группа n -й степени)
Подстановкой степени n называется взаимно однозначное отображение множества M ={1, 2,..., n} на себя. Под-
становку степени n удобно записывать в виде таблицы
1 |
2 |
... |
n |
, |
|||
a = |
α |
α |
2 |
... |
α |
|
|
|
1 |
|
|
|
n |
|
|
где под каждым элементом записан его образ и нижняя строка (α1,α2 , ... ,αn ) является некоторой перестановкой чисел
1, 2, ... , n .
Заметим, что указанное табличное изображение подстановки не однозначно, так как расположение столбцов в таблице не играет роли. Так, например,
1 |
2 |
3 |
4 2 |
1 |
3 |
4 3 |
2 |
1 |
4 |
||||
|
2 |
4 |
3 |
|
= |
4 |
2 |
3 |
|
= |
4 |
2 |
. |
|
1 |
|
1 |
3 |
1 |
||||||||
Определим на множестве подстановок степени n операцию умножения.
Определение. Произведением двух подстановок назы-
вается результат их последовательного применения, причем сначала выполняется левая подстановка, а затем - правая:
1 |
2 ... |
n α |
α ... |
α |
|
1 |
|
2 ... |
n |
||
|
α2 ... |
|
1 |
2 |
|
n |
= |
|
β2 ... |
. |
|
α1 |
αn |
β1 |
β2 ... |
βn |
β1 |
|
βn |
||||
Пример 6. Найдем произведение подстановок |
|||||||||||
|
|
1 2 3 4 |
|
|
|
1 2 3 4 |
|
||||
|
a = |
|
|
, |
|
b = |
|
|
. |
|
|
|
|
2 3 4 1 |
|
|
|
4 3 2 1 |
|
||||
В силу определения имеем: |
|
1 |
2 |
3 |
4 |
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
1 2 3 4 1 2 3 4 |
= |
↓ ↓ ↓ ↓ |
1 2 3 4 |
||||||||
ab = |
|
|
|
|
2 3 4 1 |
= |
. |
||||
2 3 4 1 4 3 2 1 |
|
↓ |
↓ |
↓ |
↓ |
3 2 1 4 |
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
3 |
2 |
1 |
4 |
|
|
Перемножим теперь подстановки a и b в обратном порядке:
8 |
9 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
1 |
2 |
3 |
4 1 |
2 |
3 |
4 |
= |
↓ ↓ ↓ ↓ |
1 |
2 |
3 |
4 |
|||||
ba = |
|
|
|
|
|
|
|
|
4 |
3 |
2 |
1 |
= |
|
|
. |
|
|
4 |
3 |
2 |
1 |
2 |
3 |
4 |
1 |
|
↓ ↓ ↓ ↓ |
1 |
4 |
3 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
1 |
4 |
3 |
2 |
|
|
|
|
Замечаем, что ab ≠ ba . Следовательно, операция умножения подстановок некоммутативна.
Опишем свойства операции умножения.
1) Операция умножения подстановок ассоциативна.
Доказательство. Пусть
1 |
2 |
... |
n |
, |
||
a = |
|
α2 |
... |
|
|
|
α1 |
αn |
|
||||
α1 α2 |
... |
αn |
|
|
||
b = β |
β |
... |
β |
|
, |
|
|
1 |
2 |
|
n |
|
|
β |
β |
... |
β |
|
||
c = |
γ1 |
γ2 |
... |
γn |
|
|
|
1 |
2 |
|
n |
||
-три произвольные подстановки степени n . Вычислим (ab)c :
ab = |
1 |
2 |
... |
n α |
α |
... |
α |
|
1 |
2 |
... |
n |
, |
||||
|
|
α2 |
... |
|
1 |
2 |
... |
n |
= |
β2 |
... |
|
|
||||
|
α1 |
αn β1 |
β2 |
βn |
|
β1 |
βn |
|
|||||||||
|
1 |
2 |
... |
n β |
β |
... |
β |
|
1 |
2 |
... |
n |
|
||||
(ab)c = |
β |
β |
... |
β |
γ1 |
γ2 |
... |
γn |
= γ |
γ |
2 |
... |
γ |
. |
|||
|
|
1 |
2 |
|
n |
1 |
2 |
|
n |
1 |
|
|
|
n |
|
||
Теперь вычислим a(bc) :
bc = |
α1 |
α2 |
... |
αn |
β1 |
β2 |
... |
βn |
|
α1 |
α2 |
... |
αn |
|
|||||||
|
β |
β |
... |
β |
γ |
γ |
2 |
... |
γ |
n |
= |
γ |
γ |
2 |
... |
γ |
|
, |
|||
|
|
1 |
2 |
|
n |
|
1 |
|
|
|
|
1 |
|
|
|
n |
|
||||
|
1 |
2 |
... |
n α |
α |
... |
α |
|
1 |
|
2 |
... |
n |
|
|||||||
a(bc) = |
α2 |
... |
|
1 |
|
2 |
... |
|
n |
= |
γ2 |
... |
|
. |
|||||||
|
α1 |
αn |
γ1 |
γ2 |
γn |
γ1 |
γn |
|
|||||||||||||
Таким образом, (ab)c = a(bc) , т.е. умножение подстановок
ассоциативно.
2) Существование нейтрального элемента.
Подстановка
1 |
2 ... |
n |
, |
e = |
2 ... |
|
|
1 |
n |
|
переводящая каждое число в себя, называется тождественной (или единичной) подстановкой и выполняет роль единицы при умножении подстановок. Действительно, для любой подстановки a имеем ae = ea = a (проверьте!).
3) Существование обратной подстановки.
Для каждой подстановки
1 |
2 |
... |
n |
|||
a = |
α |
α |
2 |
... |
α |
|
|
1 |
|
|
|
n |
|
существует обратная подстановка
a−1 |
|
α |
α |
2 |
... |
α |
n |
|
, |
= |
1 |
|
... |
|
|
||||
|
|
1 |
2 |
n |
|
|
|||
которая получается из a переменой мест верхней и нижней строк. Действительно, легко проверить, что aa−1 = a−1a = e .
4) Операция умножения подстановок некоммутатив-
на, т.е. в общем случае ab ≠ ba . Этот факт уже отмечался в примере 6.
10 |
11 |

Вывод. Из свойств 1) - 3) следует, что множество подстановок с операцией умножения является группой. Она называется симметрической группой подстановок степени n и обозначается Sn .
Отметим, что Sn - это конечная группа, её порядок | Sn |= n!, так как число различных подстановок из n элемен-
тов равно n!.
Свойство 4 означает, что группа Sn не является абелевой при n > 2 . При n = 2 группа S2 состоит из двух элемен-
1 |
2 |
и a |
|
1 |
2 |
|
, причем |
ae = ea = a |
(проверь- |
тов e = |
|
= |
2 |
1 |
|
||||
1 |
2 |
|
|
|
|
|
|
||
те!). Следовательно, |
S2 |
- абелева. При n =1 получаем груп- |
|||||||
1
пу S1 , состоящую из одного нейтрального элемента e = .
1
Пример 7. Рассмотрим симметрическую группу третьей степени S3 . Эта группа состоит из 3!=6 различных под-
становок. Обозначим их следующим образом:
a1 |
1 2 |
3 |
|
, |
a2 |
1 |
2 |
3 |
|
a3 |
1 |
2 |
3 |
||||
= |
|
3 |
|
= |
3 |
|
, |
|
= |
1 |
, |
||||||
|
1 2 |
|
|
|
1 |
2 |
|
|
2 |
3 |
|||||||
a4 |
1 |
2 |
3 |
, |
a5 |
1 |
2 |
3 |
, |
a6 |
1 |
2 |
3 |
||||
= |
3 |
1 |
|
= |
|
1 |
|
|
= |
|
2 |
. |
|||||
|
2 |
|
|
|
3 |
|
2 |
|
|
3 |
1 |
||||||
Составим таблицу умножения (таблицу Кэли) для группы S3 (проверьте!):
|
|
i |
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
|
|
a6 |
|
|
|
|
a1 |
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
|
|
a6 |
|
|
|
|
a2 |
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
a3 |
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
a4 |
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
a5 |
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
a6 |
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
a1 |
|
|
Как уже отмечалось, группа S3 некоммутативна, поэтому
полученная таблица Кэли несимметрична относительно главной диагонали.
Подстановки бывают двух видов: четные и нечетные. Напомним, что подстановка называется четной, если ее
верхняя и нижняя строки имеют одинаковую четность, и нечетной в противном случае.
Теорема 1. Произведение двух подстановок одинаковой четности является четной подстановкой, а произведение двух подстановок разной четности - нечетной подстановкой.
Доказательство. Рассмотрим произведение двух под-
|
|
α1 |
α2 ... |
αn |
|
|
β1 |
|
β2 ... |
|
βn |
|
|
||||||||||
становок a = |
β |
β ... |
β |
|
и b = |
γ |
1 |
|
γ |
2 |
|
... |
|
γ |
. Имеем: |
||||||||
|
|
|
1 |
|
2 |
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
||||
α1 |
α2 |
... |
αn |
β1 |
β2 ... |
βn |
|
α1 |
α2 |
... |
αn |
||||||||||||
ab = |
β |
β |
|
... |
β |
γ |
1 |
γ |
2 |
... |
γ |
|
|
= |
γ |
1 |
γ |
2 |
... |
γ |
. |
||
|
1 |
2 |
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
n |
||||||
Возможны следующие случаи.
1 случай. Пусть подстановки a и b имеют одинаковую четность, т.е. либо они обе четны, либо обе нечетны. Покажем, что их произведение ab является четной подстановкой.
а) Пусть a и b - четные подстановки. Тогда переста-
новки (α1,α2, ... ,αn) и (β1,β2, ... ,βn) , а также (β1,β2, ... ,βn) и (γ1,γ2, ... ,γn) имеют одинаковую четность. Следовательно,
12 |
13 |
(α1,α2, ... ,αn) и (γ1,γ2, ... ,γn) тоже будут одинаковой четно-
сти; а значит произведение ab - четная подстановка.
б) Пусть a и b - нечетные подстановки. Тогда переста-
новки (α1,α2, ... ,αn) и (β1,β2, ... ,βn) , а также (β1,β2, ... ,βn) и (γ1,γ2, ... ,γn) разной четности. Следовательно, (α1,α2, ... ,αn)
и (γ1,γ2, ... ,γn) будут одинаковой четности; а значит произ-
ведение ab - четная подстановка.
2 случай. Пусть подстановки a и b имеют разную четность, т.е. либо a - нечетная, b - четная; либо наоборот: a - четная, b - нечетная. Покажем, что их произведение ab - нечетная подстановка.
а) Пусть a - нечетная подстановка, b - четная. Тогда перестановки (α1,α2, ... ,αn) и (β1,β2, ... ,βn) - разной четно-
сти, а перестановки (β1,β2, ... ,βn) и (γ1,γ2, ... ,γn) - одинаковой четности. Следовательно, перестановки (α1,α2, ... ,αn) и (γ1,γ2, ... ,γn) имеют разную четность.
Такой же результат получаем и в случае б): если a - четная, b - нечетная (докажите самостоятельно). Следовательно, если подстановки a и b имеют разную четность, то их произведение ab - нечетная подстановка. ■
Следствие. Множество всех четных подстановок степени n образует группу.
Доказательство. Проверим три аксиомы группы.
1) В силу теоремы 1 произведение двух четных подстановок является четной подстановкой, значит умножение является бинарной операцией. Причем эта операция ассоциативна.
2) Существует нейтральный элемент e = 1 |
2 ... |
n |
|
- |
1 |
2 ... |
n |
|
|
четная подстановка.
3) Для любой четной подстановки |
|
α1 α2 |
... |
αn |
||||||||||||
a = |
β |
β |
|
... |
β |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
n |
существует обратная |
a |
−1 |
β1 |
β2 |
... |
βn |
. Причем |
a |
−1 |
так- |
||||||
|
= α |
α |
|
... |
α |
|
|
|||||||||
|
|
|
1 |
|
2 |
|
|
n |
|
|
|
|
|
|
|
|
же является четной подстановкой, так как четность её нижней и верхней строк одинаковая (такая же, как и в подстановке a ). ■
Группа четных подстановок обозначается An и называется знакопеременной группой степени n . Эта группа конечная, ее порядок | An |= n! 2 .
2 .
Отметим, что множество всех нечетных подстановок степени n группу не образует, так как в силу теоремы 1 в этом множестве операция умножения не является бинарной. Действительно, перемножая две нечетные подстановки, получаем четную, которая уже не принадлежит рассматриваемому множеству нечетных подстановок.
Контрольные вопросы и задания к п. 1.2
1.Как определяется произведение двух подстановок?
2.Какими свойствами обладает операция умножения подстановок?
3.Что называется симметрической группой и чему равно число ее элементов?
4.Является ли симметрическая группа абелевой?
5.Сформулируйте теорему о четности произведения двух подстановок.
6.Докажите, что множество всех четных подстановок степени n образует группу. Чему равен порядок этой группы?
7.Образует ли группу множество всех нечетных подстановок степени n ?
14 |
15 |
8. Приведите пример подстановки a Sn , для которой:
а) a = a−1 ; |
б) a3 = e . |
|
|
|
|
|
|
|
|
|||
9. Для данных |
подстановок |
a,b S10 |
найдите ab , ba , |
|||||||||
(ab)−1 , (ba)−1 : |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
||
a = |
8 |
10 |
1 |
2 |
6 |
3 |
4 |
5 |
9 |
7 |
|
, |
|
|
|
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
||
b = |
9 |
8 |
1 |
10 |
2 |
6 |
7 |
4 |
3 |
5 |
. |
|
|
|
|
||||||||||
10. Найдите подстановку X из уравнения aXb2 = c , где
1 |
2 |
3 |
4 |
5 |
6 |
7 |
, |
||
a = |
7 |
3 |
2 |
1 |
6 |
5 |
4 |
|
|
|
|
|
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
, |
|
b = |
3 |
1 |
2 |
7 |
4 |
5 |
6 |
|
|
|
|
|
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
c = |
5 |
1 |
3 |
6 |
4 |
7 |
2 |
. |
|
|
|
|
|||||||
1.3.Разложение подстановки в произведение независимых циклов
Разложим подстановки группы Sn в произведение бо-
лее простых подстановок. Идею разложения сначала поясним схематически на примере. Пусть a,b S4 и
1 |
2 |
3 |
4 |
, |
1 |
2 |
3 |
4 |
||
a = |
2 |
3 |
4 |
|
b = |
4 |
3 |
2 |
. |
|
|
1 |
|
|
1 |
||||||
Подстановка a - это отображение, которое действует следующим образом: 1 → 2 , 2 →3 , 3 → 4 , 4 →1. Изобразим это отображение на схеме:
Для подстановки b получим такую схему:
Тогда подстановку a кратко можно записать |
в виде: |
|
a = (1, 2,3, 4) |
- это цикл длины 4, а подстановку b |
в виде |
b = (1, 4)(2,3) |
- это произведение двух независимых циклов |
|
длины 2. |
|
|
Перейдем к строгим определениям.
16 |
17 |
Определение. Пусть M = (α1,α2 , ... ,αn ) - это некото-
рая перестановка чисел 1, 2, … , n . Циклом длины k называется такое отображение f множества M на себя, при кото-
ром f (α1) =α2 , f (α2 ) =α3 , … , f (αk−1) =αk , f (αk ) =α1 и f (αi ) =αi αi ≠α1,α2 ,...,αk .
Цикл длины k обозначается (α1,α2 , ... ,αk ) .
Другими словами, цикл длины k - это такая подстановка, которая перемещает элементы, записанные в цикле, а остальные элементы оставляет на своих местах, т.е. цикл в развернутом виде запишется так:
(α ,α |
, ... ,α |
k |
) = |
α1 |
α2 |
... |
αk−1 |
αk |
αk+1 |
... |
αn . |
|||||
1 2 |
|
|
α |
2 |
α |
3 |
... |
α |
k |
α |
α |
k+1 |
... |
α |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
n |
||||
Отметим, что при цикловой записи подстановки образ элемента αr записывается не под ним, а справа от него.
Длина цикла - это число символов в цикле, т.е. число перемещаемых символов.
Элементы, которые записаны в цикле длины ≥ 2 , называются мобильными элементами подстановки, остальные элементы называются неподвижными.
Два цикла называются независимыми, если они не имеют общих символов.
Полезно иметь ввиду, что цикл длины k может быть записан k различными способами, а именно:
|
|
|
(α1,α2 , ... ,αk−1,αk ) = (α2 ,α3, ... ,αk ,α1) = |
|
|
|
= (α3,α4 , ... ,αk ,α1,α2 ) = ... = (αk ,α1,α2 , ... ,αk−1) . |
||
|
|
В |
рассмотренном выше примере для подстановки |
|
1 |
2 |
3 |
4 |
|
b = |
4 |
3 |
2 |
была получена другая запись в виде произве- |
|
1 |
|||
дения независимых циклов: |
b = (1, 4)(2,3) , |
или |
записывая |
||||
циклы в развернутом виде (т.е. в виде таблиц) получим: |
|||||||
1 |
2 |
3 |
4 1 |
2 |
3 |
4 |
|
b = (1, 4)(2,3) = |
2 |
3 |
|
3 |
2 |
4 |
. |
4 |
1 1 |
|
|||||
Нетрудно убедится, что в этой записи сомножители можно переставлять местами, т.е. верно
b = (1, 4)(2,3) = (2,3)(1, 4) .
Теорема 2. При перемножении независимых циклов порядок множителей не влияет на результат.
Практически разложение подстановки в циклы осуществляется следующим образом: начинаем с любого из перемещаемых символов и выписываем за ним те символы, в которые он переходит при повторении подстановки, пока не вернемся к исходному символу. После этого "закрытия" цикла начинаем с одного из оставшихся перемещаемых символов, получаем второй цикл и т.д. Продолжая этот процесс до исчерпания всех элементов, мы получим цикловую запись подстановки a Sn :
a = (α1,α2 ,...,αk )(β1, β2 ,..., βs ) ... (γ1,γ2 ,...,γm ) .
Заметим, что при n ≥ 2 цикловая запись подстановки не единственна, так как первый элемент каждого цикла в общем случае может выбираться неоднозначно, и кроме того независимые циклы можно переставлять местами (в силу теоремы 2).
Теорема 3. Любую нетождественную подстановку группы Sn можно разложить в произведение независимых
циклов длины ≥ 2 , и такое представление единственно с точностью до перестановки сомножителей.
18 |
19 |
