1813

Таким образом, оба условия из определения подгруппы выполнены, следовательно, множество N (a) является под-

группой в G . ■

Определение. Пересечение нормализаторов всех элементов группы G называется центром группы и обозначается C(G) .

Из определения вытекает, что центр группы состоит из всех тех элементов, каждый из которых коммутирует со всеми элементами группы, т.е.

C(G) = ∩ N(a) ={h G | ha = ah a G}.

a G

Пример 46. В группе G = GLn ( ) невырожденных

матриц центр образует множество скалярных матриц, т.е. C(G) ={λE, гдеλ }, здесь E - единичная матрица n -го по-

рядка.

Отметим, что:

1)центр C(G) всегда непуст, так как e C(G) ;

2)центр C(G) является подгруппой группы G (как пересечение подгрупп);

3)центр группы является ее нормальным делителем, так как h C(G) и g G верно

g−1hg = g−1 (hg) = g−1 (gh) = (g−1g)h = h C(G) ,

т.е. вместе с каждым элементом h центр группы содержит и все сопряженные с ним элементы.

1.18.Теорема о числе элементов в классах сопряженных элементов

Используя понятия, введенные в предыдущем пункте, докажем следующее утверждение.

Теорема 24. Число элементов в каждом классе сопряженных между собой элементов конечной группы является делителем порядка группы.

Доказательство. Пусть G - произвольная конечная группа и a G . Рассмотрим нормализатор N(a) элемента a ,

т.е. N (a) ={x G : xa = ax}. В силу теоремы 23 множество N (a) является подгруппой в G . Рассмотрим разложение группы G на правые смежные классы по подгруппе N(a) ,

т.е. G = N (a)g . Докажем, что между этими классами и

g G

элементами, сопряженными с a , существует взаимно однозначное соответствие. Для этого покажем, что если два элемента x и y принадлежат одному и тому же правому смеж-

ному классу N(a)g , то элементы x−1ax и y−1ay совпадают,

y = h2 g = h2 (h1−1x) = (h2h1−1)x = hx ,

где обозначено h = h2h1−1 , причем элемент h N (a) , так как N (a) - подгруппа и вместе с каждой парой своих элементов

содержит их произведение. Таким образом, если элементы x, y N (a)g , то они связаны соотношением y = hx , где h -

некоторый элемент из N (a) .

Обозначим b = x−1ax и c = y−1ay . Покажем, что b = c . Для элемента c имеем:

c = y−1ay = (hx)−1a(hx) = x−1h−1(ah)x ,

но элемент h N(a) , поэтому ah = ha . Тогда

c = x−1h−1(ha)x = x−1(h−1h)ax = x−1ax = b .

Тем самым доказано, что все элементы, принадлежащие одному и тому же смежному классу N(a)g , порождают

один и тот же элемент b , сопряженный с элементом a . Докажем в обратную сторону. Пусть элементы p, q G

таковы, что p−1ap = b и q−1aq = b , т.е. элементы p и q порождают один и тот же элемент, сопряженный с a . Из вто-

( pq−1)−1a( pq−1) = (q−1)−1 p−1a( pq−1) = (qp−1)a( pq−1) =

= q( p−1ap)q−1 = qbq−1 = a .

Таким образом, ( pq−1)−1a( pq−1) = a . Умножим обе части этого равенства на pq−1 слева, получим a( pq−1) = ( pq−1)a . Последнее означает, что элемент pq−1 коммутирует с эле-

тогда p и q принадлежат одному и тому же правому смежному классу N (a)q = N (a) p .

Итак, доказано взаимно однозначное соответствие между правыми смежными классами группы G по подгруппе

N (a) и элементами, сопряженными с a . А именно, доказано, что все элементы x , принадлежащие одному классу N (a)g , порождают один и тот же элемент b = x−1ax , и об-

ратно. Следовательно, число правых смежных классов равно числу различных элементов, сопряженных с a . Но в силу теоремы Лагранжа (см. п. 1.11) число смежных классов является делителем порядка группы. Поэтому число элементов, сопряженных с элементом a , также является делителем порядка группы. ■

1.19.Разложение группы в прямое произведение групп

Определение. Группа G называется прямым произведением своих подгрупп H1 и H2 , если выполняются следующие условия:

1)H1, H2 являются нормальными делителями группы G ;

2)H1 ∩H2 ={e} ;

3)каждый элемент x G может быть представлен в

циклическая группа второго порядка с образующим элементом −1. Тогда группа G является прямым произведением

своих подгрупп H1 и H2 , т.е. G = + × −1 .

Опишем свойства прямого произведения. Сформулируем их в виде двух теорем.

Теорема 25. Каждый элемент группы G = H1 ×H2 однозначно представляется в виде произведения h1h2 , где

h1, g1 H1 и h2 , g2 H2 . Тогда h1h2 = g1g2 . Обе части этого равенства умножим справа на h2−1 и слева на g1−1 (т.е. соберем вместе элементы с одинаковыми индексами). Получим:

мент h1 H1 коммутирует с каждым элементом h2 H2 ,

называют коммутатором элементов h1 и h2 . Произведение его первых трех сомножителей h1−1h2−1h1 H2 , так как H2 -

нормальный делитель и поэтому вместе с каждым элементом h2−1 H2 содержит все сопряженные с ним элементы. А так как H2 является подгруппой, то элемент

z= (h1−1h2−1h1)h2 H2 .

Сдругой стороны, для произведения трех последних

Обе части последнего равенства умножим слева на h2h1 , получим h1h2 = h2h1 . Таким образом, любой элемент из H1 коммутирует с любым элементом из H2 . ■

Пусть G = H1 ×H2 и элементы g, g′ G . Тогда в силу

определения и свойств прямого произведения (теоремы 25, 26) имеем:

g = h1h2 , g′ = h1′h2′ , где hi , hi′ Hi , i =1, 2 ; g g′ = h1(h2h1′)h2′ = h1(h1′h2 )h2′ = h1h1′ h2h2′ ;

g−1 = (h1h2 )−1 = h2−1h1−1 = h1−1h2−1 .

Таким образом, операции умножения элементов и взятия обратного элемента в прямом произведении групп выполняются покомпонентно. Отсюда следует, что изучение свойств группы G = H1 ×H2 сводится к изучению свойств ее прямых

сомножителей. В частности, группа G = H1 ×H2 абелева тогда и только тогда, когда подгруппы H1 и H2 - абелевы.

Определение. Группа G называется разложимой, если существуют ее подгруппы H1 и H2 , отличные от G (а потому и от {e} ) такие, что выполняется равенство

G= H1 ×H2 .

Впротивном случае группа G называется неразложи-

мой.

Приведем пример неразложимой циклической группы.

Теорема 27. Группа ( , +) неразложима.

Доказательство. Предположим, что группа ( , +) разложима в прямую сумму отличных от нее подгрупп H1 и H2 . Тогда H1 , H2 - ненулевые подгруппы и существуют натуральные числа m H1 и n H2 . Рассмотрим число mn ≠ 0 , оно содержится в каждой из подгрупп в силу их замкнутости по сложению, а значит mn H1 ∩H2 . Но по условию H1 ∩H2 ={0}, и мы пришли к противоречию с неравенством mn ≠ 0 . Противоречие означает, что группа ( , +)

неразложима. ■

Определение. Внешним прямым произведением произ-

вольных групп G1, ... ,Gn называется группа (G, ) , в которой множество G есть декартово произведение G = G1 ×...×Gn , а умножение элементов a = (a1, ... , an ) G и b = (b1, ... ,bn ) G задается равенством: ab = (a1b1, ... , anbn ) , где элементы ai , bi перемножаются по правилу умножения в

группе Gi , i =1, n .

Обозначается эта группа так: G = G1 ... Gn . Заметим, что группы G1, ... ,Gn не являются подгруп-

пами в G .

Если операция в группе обозначается знаком + , то G называется внешней прямой суммой групп G1, ... ,Gn и обо-

значается как G = G1 ... Gn .

Особый интерес представляет строение конечных абелевых групп. Соответствующие результаты будут приведены ниже в параграфе 2.

1.20.Гомоморфизм групп. Ядро гомоморфизма

Пусть G1 и G2 - две мультипликативные группы. Напомним (см. п. 1.6), что отображение ϕ : G1 →G2 называетя гомоморфизмом, если ϕ(xy) =ϕ(x)ϕ( y) x, y G1 .

Отметим, что в данном определении мы не требуем взаимной однозначности отображения ϕ .

Напомним некоторые свойства гомоморфизма.

1)ϕ(e1) = e2 , где e1 и e2 - нейтральные элементы групп G1 и G2 соответственно;

2)ϕ(x−1) = (ϕ(x))−1 .

Приведем примеры гомоморфизмов.

кативная группа поля действительных чисел. Тогда отображение: ϕ : G1 →G2 , действующее по правилу ϕ(A) =| A | является гомоморфизмом, так как

ϕ( AB) =| AB |=| A | | B |=ϕ( A)ϕ(B) .

Причем данное отображение ϕ не является взаимно однозначным, и, следовательно, не является изоморфизмом.

Из таблиц Кэли видно, что в одинаковых клеточках таблиц находятся соответственные элементы, поэтому равенство ϕ(xy) =ϕ(x)ϕ(y) выполняется для всех x, y G1 . Следова-

тельно, отображение ϕ - гомоморфизм.

Пусть ϕ : G1 →G2 - гомоморфизм. Известно (см. свойство 1), что при всяком гомоморфизме нейтральный элемент группы G1 отображается в нейтральный элемент группы G2 . Но, кроме того, в нейтральный элемент группы G2 могут отображаться и какие-то другие элементы из G1 .

Определение. Ядром гомоморфизма ϕ : G1 →G2 назы-

вается множество всех элементов группы G1 , которые отображаются в нейтральный элемент группы G2 .

Ядро гомоморфизма ϕ обозначают Kerϕ . Таким обра-

зом,

Kerϕ ={x G1 : ϕ(x) = e2} ,

где e2 - нейтральный элемент группы G2 .

Например, для гомоморфизма ϕ из примера 50 имеем

Kerϕ ={e, a2 , a4}.

Опишем некоторые свойства ядра.

Теорема 28. Ядро гомоморфизма Kerϕ является нормальным делителем группы G1 .

Доказательство. Покажем сначала, что Kerϕ - подгруппа в G1 . Пусть x, y Kerϕ , т.е. ϕ(x) =ϕ( y) = e2 . Тогда

ϕ(xy) =ϕ(x)ϕ( y) = e2 e2 = e2 ;

ϕ(x−1) = (ϕ(x))−1 = e2−1 = e2 .

Таким образом, xy и x−1 Kerϕ . Следовательно, Kerϕ является подгруппой группы G1 .

Покажем теперь, что подгруппа Kerϕ вместе с каждым элементом содержит все сопряженные с ним элементы.

Пусть x Kerϕ , т.е. ϕ(x) = e2 . Рассмотрим сопряжен-

ный с x элемент g−1xg , где g G1 . В силу определения и свойств гомоморфизма имеем:

любого g G1 . Следовательно, в силу теоремы 18 подгруппа Kerϕ является нормальным делителем группы G1 . ■

Теорема 29. Если Kerϕ ={e1}, то ϕ является изомор-

физмом.

Доказательство. Покажем, что отображение ϕ является взаимно однозначным. Пусть ϕ(a) =ϕ(b) для некоторых

элементов a,b G1 . Тогда для элемента ab−1 имеем

ϕ(ab−1) =ϕ(a)ϕ(b−1) =ϕ(a)(ϕ(b))−1 =ϕ(a) (ϕ(a))−1 = e2 .

Значит, ab−1 Kerϕ . Но по условию ядро Kerϕ состоит

только из нейтрального элемента, поэтому ab−1 = e1 . Откуда

в силу единственности обратного элемента имеем a = b . Следовательно, гомоморфизм ϕ является взаимно одно-

значным отображением, а значит ϕ - изоморфизм. ■

1.21. Теорема о гомоморфизмах

Одной из основных в теории групп является следующая теорема о гомоморфизмах.

Теорема 30. Пусть ϕ - гомоморфизм группы G1 на группу G2 и Kerϕ - ядро этого гомоморфизма. Тогда факторгруппа G1 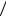Kerϕ изоморфна группе G2 .

ми G1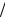Kerϕ и G2 , обладающее свойством f (xy) = f (x) f ( y)

x, y G1 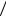Kerϕ .

Фактор-группа G1 Kerϕ , состоит из смежных классов a Kerϕ . Отображение f : G1Kerϕ →G2 определим следующим образом:

f (a Kerϕ) =ϕ(a) ,

т.е. каждому смежному классу a Kerϕ поставим в соответ-

ствие образ элемента a , который порождает этот класс. Покажем, что отображение f определено корректно,

a Kerϕ = a1 Kerϕ . Следовательно, для построенного отображения f должно выполнятся:

ϕ(a) = f (a Kerϕ) = f (a1 Kerϕ) =ϕ(a1) .

Покажем, что равенство ϕ(a) =ϕ(a1) действительно верно. Так как a1 a Kerϕ , то найдется такой элемент h Kerϕ ,

что a1 = ah . Тогда ϕ(a1) =ϕ(ah) =ϕ(a)ϕ(h) =ϕ(a)e2 =ϕ(a) .

классов имеем

xy = (a Kerϕ)(b Kerϕ) = (ab) Kerϕ .

Тогда по определению отображения f получим

f(xy) = f ((ab) Kerϕ)) =ϕ(ab) =ϕ(a)ϕ(b) =

=f (a Kerϕ) f (b Kerϕ) = f (x) f ( y) .

Таким образом, f (xy) = f (x) f ( y) x, y G1 Kerϕ , т.е. f является гомоморфизмом.

Покажем теперь, что f - взаимно однозначное отображение. Рассмотрим произвольный элемент y G2 . Так как ϕ - это отображение "на", то существует элемент x G1 такой, что ϕ(x) = y . Предположим, что существует еще один элемент x G1 такой, что ϕ(x) = y . Напомним, что ϕ - гомоморфизм, а значит ϕ не является взаимно однозначным отображением, и поэтому такая ситуация возможна. Имеем ϕ(x) =ϕ(x) , где x, x G1 . Тогда в силу определения обрат-

ного элемента и свойств гомоморфизма получим:

e2 = (ϕ(x))−1 ϕ(x) = (ϕ(x))−1 ϕ(x) =ϕ(x−1)ϕ(x) =ϕ(x−1x) ,

откуда ϕ(x−1x) = e2 . Следовательно, x−1x Kerϕ . Отсюда вытекает, что x x Kerϕ , тогда в силу свойств смежных

классов x Kerϕ = x Kerϕ . Итак, из равенства ϕ(x) =ϕ(x) по определению отображения f получаем f (xKerϕ) = f (xKerϕ). Кроме того, по доказанному x Kerϕ = x Kerϕ , что и означает

любого действительного числа a можно указать диагональ-

этого гомоморфизма является множество матриц, определитель которых равен единице: Kerϕ ={A : | A |=1} .

Рассмотрим фактор-группу G1 Kerϕ . Каждый смеж-

ный класс, как было показано в примере 40, состоит из матриц, имеющих один и тот же определитель, причем нет матриц с нулевым определителем. Таким образом, между множеством смежных классов и множеством ненулевых действительных чисел можно установить взаимно однозначное

Контрольные вопросы и задания к п. 1.20-1.21

1.Что такое гомоморфизм групп? Приведите примеры.

2.Что называется ядром гомоморфизма групп?

3.Докажите, что ядро гомоморфизма является подгруппой.

4.Докажите, что ядро гомоморфизма является нормальным делителем.

5.Какому условию должно удовлетворять ядро гомоморфизма, чтобы он был изоморфизмом?

6.Сформулируйте теорему о гомоморфизмах.

7.Пусть C =C \{0} и R = R \{0}. Покажите, что отображение ϕ:C →R , действующее по правилу ϕ(z) =| z | , явля-

ется гомоморфизмом групп. Найдите ядро этого гомоморфизма.

8.Пусть G1 = (R, +) - аддитивная группа действительных чи-

сел и G2 - мультипликативная группа комплексных чисел,

модуль которых равен единице. Докажите, что отображение ϕ: G1 →G2 , ϕ(x) =cos x +isin x , является гомоморфиз-

мом. Найдите ядро этого гомоморфизма.

§ 2. КОНЕЧНЫЕ АБЕЛЕВЫ ГРУППЫ

Из предыдущего параграфа видно, что условие коммутативности группы существенно облегчает изучение многих ее сойств. Это наводит на мысль о целесообразности отдельного изучения коммутативных групп. В настоящее время теория абелевых групп развита весьма глубоко, однако полного описания их строения не существует. В данном параграфе дается полное описание строения лишь конечных абелевых групп.

Ниже мы будем рассматривать конечные абелевы группы, причем будем пользоваться аддитивной записью и соответствующей терминологией. Операцию в группе будем называть сложением и обозначать знаком +; нейтральный элемент e будем называть нулем группы и обозначать 0 ; вместо обратного элемента будем говорить о противополож-

будем говорить "прямая сумма" и для обозначения прямой суммы будем использовать знак .

Наша цель - представить конечную абелеву группу в виде прямой суммы простейших групп, какими являются циклические. При этом на порядки циклических групп будут наложены ограничения, так как в противном случае разложение группы в прямую сумму - неоднозначно.

2.1. Аннулятор элемента и аннулятор группы

Для дальнейших рассуждений нам потребуются понятия аннулятора элемента и аннулятора группы. Сформулируем соответствующие определения и опишем свойства аннуляторов.

Пусть (G, +) - конечная абелева группа и элемент

a G .

Определение. Аннулятором элемента a G называет-

ся такое натуральное число m , что ma = 0 .

Из определения вытекает, что среди аннуляторов найдется минимальный и он равен порядку элемента a .

Пример 52. Пусть G = ( 2 , +) - аддитивная группа вычетов по модулю 2, т.е. G состоит из двух элементов 0 и 1 .

Для элемента 0 аннулятором является любое натуральное число, так как

m0 = 0 + 0 +... + 0 = 0 m .

m раз

Для элемента 1 аннуляторами будут четные числа 2, 4,6,..., так как

m1 = 1 + 1 +... + 1 = 0 при четных m ;

m раз

причем наименьший аннулятор равен 2 и является порядком

элемента 1 .

Теорема 31. Все аннуляторы элемента a G делятся на его порядок.

Доказательство. Пусть k = ord a , и m - какой-либо аннулятор элемента a . Тогда в силу соответствующих определений k ≤ m . Поделим m на k . В силу теоремы о делении с остатком получим

m = kq +r , где 0 ≤ r < k .

Выразим остаток:

r = m −kq .

Обе части этого равенства умножим на a , получим: ra = (m −kq)a = ma −kqa .

Но число k - порядок элемента a , поэтому ka = 0 ; число m - аннулятор элемента a , поэтому ma = 0 . Тогда ra = 0 −0 = 0 . Кроме того, для числа r имеем r < k ≤ m , и значит r не может быть аннулятором элемента a . Поэтому из равенства ra = 0 следует, что r = 0 .

Таким образом, m = kq . Это означает, что аннулятор m

делится на k = ord a . ■

Определение. Аннулятором группы G называется та-

кое натуральное число m , при умножении на которое аннулируются все элементы группы, т.е. ma = 0 a G .

Отметим, что порядок группы является ее аннулятором, т.е. если n =| G | , то na = 0 a G .

Покажем, что это утверждение верно для n = 2 . Пусть | G |= 2 , тогда G ={0, a} - циклическая группа второго по-

рядка, причем a ≠ 0 . Вычислим 2 0 = 0 +0 = 0 , значит n = 2 является аннулятором элемента 0 . Для элемента a произведение 2a может быть равно либо 0 , либо a . Если 2a = 0 , то n = 2 является аннулятором элемента a ; если же 2a = a , то это означает, что a +a = a a = 0 , чего быть не может. Таким образом, аннулятор элементов 0 и a равен 2 и совпадает с порядком группы.

Утверждение для n = 3 докажите самостоятельно.

2.2.Теоремы о разложении конечной абелевой группы

Сформулируем первую из теорем о разложении конечной абелевой группы в прямую сумму.

Теорема 32 (о разложении конечной абелевой группы в прямую сумму двух подгрупп). Пусть m - аннулятор группы G и m = m1m2 , причем числа m1 и m2 взаимно просты. Тогда группа G разлагается в прямую сумму двух своих подгрупп, одна из которых имеет аннулятор m1 , а другая - аннулятор m2 .

Доказательство. Пусть G1 - множество всех элементов группы G , которые аннулируются числом m1 , и G2 - то же

Покажем сначала, что G1 и G2 являются подгруппами. Для любых x1, x2 G1 имеем:

m1(x1 + x2 ) = m1x1 +m1x2 = 0 +0 = 0 x1 + x2 G1 ,

m1(−x1) = m1(−1)x1 = (−1)m1x1 = (−1)0 = 0 − x1 G1 .

Следовательно, G1 является подгруппой. Аналогично доказывается, что G2 - подгруппа.

Покажем теперь, что группа G разлагается в прямую сумму своих подгрупп G1 и G2 , т.е. что: 1) G1 и G2 являются нормальными делителями; 2) для любого g G возможно

1) По условию G - абелева группа, а значит все ее подгруппы, в том числе G1 и G2 , являются нормальными делителями.

2) По условию числа m1 и m2 - взаимно простые, т.е. НОД(m1, m2 ) =1. Тогда по теореме о линейном представлении НОД найдутся такие целые числа u1 и u2 , что m1u1 +m2u2 =1 . Умножим обе части этого равенства на произвольный элемент g G , получим

g = (m1u1 +m2u2 )g = m1u1g +m2u2 g .

числом m2 ; это означает, что g2 G2 .

Рассмотрим второе слагаемое g1 = m2u2 g . Аналогично показывается, что g1 G1 :

m1g1 = m1(m2u2 g) = (m1m2 )u2 g = (mg)u2 = 0u2 = 0 g1 G1 .

Таким образом, любой элемент g G можно предста-

g1 G1 , g2 G2 . Так как a G1 , то из равенства a = g1 + g2 вытекает, что g2 = 0 . С другой стороны a G2 , тогда из ра-