1505

4.9.5.Определение уравновешивающей силы (Fy )

спомощью рычага Жуковского

Поворачиваем план скоростей для рассматриваемого положения механизма на 90° по направлению, противоположному вращению часовой стрелки. Все внешние силы, включая и силы инерции звеньев, переносим параллельно самим себе в соответствующие точки плана (рис. 4.23).

Скорость точки приложения уравновешивающей силы

VN = ω 1Rl .

Далее составляем уравнение равновесия рычага Жуковского в следующем виде:

Fy ( pn) + G1h1 + G3h2 + Fи3h3' + +G4h4 + Fи4h4 − (Fпс − Fи5 )( pd5 ) = 0,

Fy = −G1h1 − G3h3 − Fи3h3' − G4h4 − Fи4h4' + (Fпс − Fи5 )( pt) .

( pn)

Рис. 4.23. Повернутый план скоростей

141

Таким образом, если к звеньям механизма приложены силы и моменты, то уравнение равновесия вспомогательного рычага можно написать в следующем виде:

Мощность двигателя определяется по аналогии с предыдущим примером.

4.10. Принцип виртуальных перемещений для силового расчёта

Запишем для механизма принцип виртуальных перемещений в координатной форме:

где Fxj , Fyj – проекции всех сил, приложенных к звеньям механизма, кроме реакций в кинематических парах; M zj – моменты всех сил, приложенных к звеньям; δ xj ,δ yj – виртуальные осевые перемещения точек приложения сил; δ ϕ j – виртуальные угловые перемещения звеньев механизма;

n – число сил и моментов сил. Это уравнение является основным для силового расчета. Из него получаем два вывода:

1. Для равновесия механизма в целом и в каждой его точке нельзя задавать произвольно все внешние силы, часть из них должна быть определена в процессе расчета. Такие силы называют уравновешивающими силами Fy , их число равно числу обобщенных координат механизма. Часто

определяют не уравновешивающие силы, а уравновешивающие моменты M y , так как они связаны с уравновешивающими силами простыми соот-

ношениями.

Рассмотрим механизм строгального станка с приложенной к резцу силой полезного сопротивления F5 x (рис. 4.24). Какую силу необходимо

приложить в точке B1 перпендикулярно звену AB1 , чтобы механизм находился в равновесии? Применяем принцип виртуальных перемещений:

142

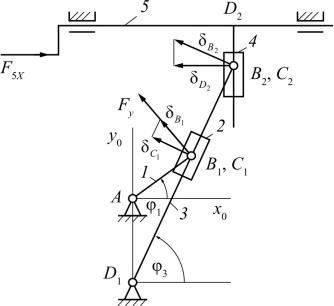
Из планов виртуальных перемещений, построенных на схеме механизма, выразим перемещение δ D2 через δ B1 :

Подставляя в (4.39), получим

Рис. 4.24. Определение уравновешивающей силы Fy из принципа виртуальных перемещений

Уравновешивающий момент найдем из соотношения

Именно этот момент надо приложить со стороны двигателя (извне), чтобы преодолеть силу полезного сопротивления. В теории механизмов принцип виртуальных перемещений редко используют непосредственно, а учитывают, что при голономных стационарных связях виртуальные перемещения совпадают с действительными перемещениями, поэтому

где Vxj , Vyj – проекции скоростей точек приложения сил; ω j – угловые скорости звеньев.

143

Сокращая затем на dt, получают с учетом (4.41)

Для механизмов с одной обобщенной координатой уравновешивающий момент находим из выражения

2. Из принципа виртуальных перемещений легко получают условия равновесия плоской системы сил. Так как в уравнении (4.38) виртуальные перемещения являются независимыми, то для равенства нулю левой части необходимо, чтобы

Такие уравнения можно составлять как для всего механизма, так и для отдельных его звеньев. В этом случае реакции связей относят к категории внешних сил. В ТММ принято вести силовой расчет погруппно, поскольку группы Ассура являются статически определимыми.

4.10.1. Условие статической определимости групп Ассура

При расчете реакции во вращательной кинематической паре (рис. 4.25) необходимо иметь в виду, что давление со стороны звена i на звено k передается частью поверхности и распределено по этой поверхности по определенному закону. При расчете мы получим не эпюру распределения давлений, а только равнодействующую Fki , которая проходит

через центр шарнира, если не учитывать трение. Неизвестными остаются модуль и направление реакции, то есть для каждой вращательной пары два неизвестных. Для поступательной кинематической пары (рис. 4.26) известно направление реакции (перпендикулярно оси поступательной пары). Неизвестными остаются модуль и точка приложения реакции, то

144

есть тоже два неизвестных. В поступательной паре может встретиться случай, когда точка приложения реакции выходит за пределы направляющей звена k или даже за пределы звена i. Пусть реакции Fik′ , Fik′′ при-

ложены в точках d ′, d ′′ (рис. 4.27) и представляют систему двух антипа-

Рис. 4.27. Распределение нагрузки в поступательной кинематической паре

Поэтому расчет элементов кинематической пары надо вести с учетом нагрузки (4.48). Может быть и такой случай, когда реакции Fik′ , Fik′′ равны и противоположны, тогда при расчете получим равнодействующую Fki , равную нулю. При этом нагрузка будет выражена в виде пары сил. Для каждого звена на плоскости можно составить три уравнения равновесия типа (4.47), а для всех звеньев – 3n уравнений. Каждая пара пятого класса

145

на плоскости дает два неизвестных параметра при определении реакции, а все пары дадут 2p5 неизвестных. Если число уравнений равновесия равно числу неизвестных, то система будет статически определимой. Условие статической определимости:

Это условие всегда удовлетворяется для групп Л.В. Ассура, поэтому удобно силовой расчет вести погруппно.

4.10.2Аналитическая статика групп Ассура второго класса

4.10.2.1.Группа второго класса первого вида

Группа состоит из двух звеньев и трех кинематических пар. Расчленим группу на два отдельных звена и будем рассматривать равновесие каждого звена. На рис. 4.28 через Si , Sk обозначены центры масс звеньев; ai , ak , α i ,α k – отрезки и углы, характеризующие положения центров масс относительно осей звеньев (ось звена рассматривается как отрезок, проведенный из центра одной кинематической пары в центр другой пары). Инерционная нагрузка для звена i находится из выражений

Рис. 4.28. Расчет группы 21

146

Аналогично для звена k:

Сюда же можно отнести и нагрузку, вызванную другими внешними силами, например, если учитывать силу тяжести звена i, то проекцию Yi следует вычислять из выражения

FBx , FBy , FDx , FDy . Реакцию во внутренней кинематической паре обозначим

учитывать, что

где

В уравнении (4.55) за полюс принята точка В. Анализ уравнений показывает, что при трех уравнениях имеем четыре неизвестных: FBx , FBy , Fxik , Fyik , то есть эти уравнения не определены.

Рассмотрим равновесие звена К:

где

147

В уравнении (4.58) за полюс принята точка О. Теперь в шести уравнениях имеем шесть неизвестных. В уравнениях (4.55) и (4.58) обозначим:

С учетом этих обозначений имеем:

a11 Fxik + a12 Fyik = b1;

(4.59)

a21 Fxik + a22 Fyik = b2 .

Из этой системы найдем Fxik , Fyik :

148

Выразив Fxik , Fyik из (4.63), (4.64), подставим полученные выражения в (4.62), найдем реакцию FD во внешней поступательной паре:

Далее последовательно находим:

Рис. 4.29. Расчет группы 22

Если реакция FD получилась неравной нулю, то из (4.65) найдем величину (DD′) :

Если же FD получилась равной нулю, то из (4.65) найдем момент в поступательной паре:

4.10.2.3.Группа второго класса третьего вида

Вэтой группе (рис. 4.30) внутренняя кинематическая пара является поступательной, реакция в ней обозначена Fik , и направлена она перпен-

дикулярно оси пары.

149

Рассмотрим равновесие звена i:

Рис. 4.30. Расчет группы 23

Выразим из (4.75) произведение (CC′)Fik , это же произведение найдем из (4.72), получим выражение для Fik .

150