1505

правилу. Полный план скоростей представлен на рис. 3.18, а. Для плана ускорений aB1 = aB2 .

По величине

Из полюса р2 плана ускорений параллельно АВ от схемы В к А откла-

Для структурной группы 23 векторные уравнения для ускорений запишутся следующим образом:

где akB3B2 – ускорение Кориолиса в движении точки В3 относительно точки В2 и вместе с ней;

arB3B2 – относительное ускорение точки В3 вокруг точки С, направлен-

из плана скоростей (см. рис. 3.18, а). В соответствии с первым уравне-

92

нием системы (3.88) b2m откладывается от точки b2, а затем из точки m проводим луч паралелльно В3С. По второму уравнению из точки С плана ускорений откладываем вектор cn1 параллельно ВС, направленный от В к С.

n

(cn ) = aB3C .

1 µa

Затем из точки n1 перпендикулярно ВС строится луч, соответствующий направлению aτB3C . На пересечении двух лучей фиксируем точку b3,

Ускорения точек S и К определяются из подобия с помощью принципа обхода контура СВК (см. рис. 3.18, б).

aS = a ( p1S ); ak = a ( p1k ).

Определяем угловое ускорение 3-го звена:

направление ε 3 показано на рис. 3.18, б.

Методики графоаналитического исследования, приведенные в примерах (рис. 3.16–3.18), применяются при кинематическом исследовании более сложных стержневых механизмов.

3.9.4. Пятизвенный стержневой механизм

Построение плана скоростей

1.VA = VC = VX = 0.

2.VB1 =VB2 ;VB1 ,VB2 (скорость перпендикулярна звену АВ),

93

При нахождении положения точки d плана скоростей используется правило обхода контура B3CD и bзсd (рис. 3.19, а).

5. V E = V X +V EX (скорость VEX параллельна х–х),

VE =VD +VED (скорость VED перпендикулярна ED).

Построение плана ускорений

1.аА = аС = аХ = 0.

2.aB1 = aB2 ; ускорения aB1 , aB2 параллельны звену АВ.

94

Графическое построение, согласно векторным уравнениям, приводится на рис. 3.19. По результатам этих построений получаем:

Положение точки d плана ускорений находится по правилу обхода контура B3CD и bзcd (см. рис. 3.19, б).

лельно неподвижной направляющей х–х).

τ

лельное звену ED; a ED – тангенцильное ускорение, перпендикулярное звену ED).

По результатам графического построения векторных уравнений

Планы скоростей и ускорений механизма в заданном положении изображены на рис. 3.19 а, б.

а

Рис. 3.19. Кинематическое исследование пятизвенного механизма: а – схема механизма; б – план скоростей; в – план ускорения

95

Максимальный ход ползуна

Текущее перемещение ползуна относительно одного из крайних положений, например, левого:

Задача о скоростях

Используя результаты решения задачи о положениях, угловую скорость шатуна можно найти дифференцированием по времени (3.91):

Задача об ускорениях

Эта задачи решается путем дифференцирования первых производных, полученных для определения скоростей:

Для определения положений центров масс звеньев (например, точка S2 шатуна) и других точек звеньев (например, точка К) записываем векторные уравнения

98

В проекциях на оси координат перемещения этих точек в соответствии с соотношениями (3.98) будут следующими:

оси АХ. Следует учесть, что φk – const. Аналогичным способом находятся ускорения точек S2 и К:

Примечание. В некоторых механизмах длина шатуна существенно больше длины кривошипа, т.е. λ2 << 1 . В этом случае для определения

99

кинематических характеристик используют приближенные, более простые по сравнению с соотношениями (3.91)–(3.100) формулы, полученные на основе разложения радикалов в ряд по формуле бинома Ньютона.

Шарнирный четырехзвенник

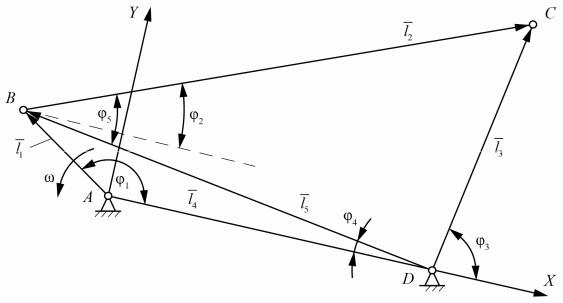
Кинематический анализ проводим для схемы механизма, представленной на рис. 3.21. Система координат выбирается так, чтобы ось АХ была направлена от точки A до D.

Уравнение замкнутого векторного контура АВСD имеет вид

Рис. 3.21. Схема шарнирного четырехзвенника

В проекциях на оси координат это уравнение записывается следующим образом:

так как φ3 = 0.

Соотношение (3.102) удобно использовать при решении задач о скоростях и ускорении. При определении же положения звеньев пользуются более удобными для решения на ЭВМ формулами.

100